
|
A1. 1
$
I = \frac{I_0}{N^2} \cdot \left( \frac{ \sin \left( Nqa/2 \right)}{ \sin \left( qa/2 \right) } \right)^2 \cdot \left( \frac{ \sin \left( qb/2 \right)}{\left( qb/2 \right) } \right)^2 $ |
0.30 |
|
|
A2. 1
$q = \frac{2\pi}{a} \cdot h, \quad h \in \mathbb{Z}$
DISCLAIMER. Here and below we use the notations: $\mathbb{Z}$ – integer numbers: $\{..., -2, -1, 0, 1, 2, ...\}$ $\mathbb{N}$ – positive numbers: $\{1, 2, ...\}$ |
0.20 |
|
| A3. 1 $q = q_1 \cdot h, \quad h \in \mathbb{Z}$ | 0.10 |
|
| A3. 2 $q_1 \cdot a = 2\pi$ | 0.10 |
|
| A4. 1 Scheme of setup | 0.10 |
|
| A4. 2 Formula for calculation $q_1 = \frac{2\pi s_1}{L \lambda}$ or $a=\frac{\lambda L}{s_1}$, $s_1$ is distance between the two nearest reflexes on screen. | 0.10 |
|
| A4. 3 DG1: $ q_1 = 315 \pm 22 \mathrm{~mm^{-1}} $ | 0.08 |
|
| A4. 4 DG1: $a = 19.7 \pm 1.3 \mathrm{~\mu m} $ | 0.08 |
|
| A4. 5 DG2: $ q_1 = 125 \pm 10 \mathrm{~mm^{-1}} $ | 0.08 |
|
| A4. 6 DG2: $ a = 49.2 \pm 3.2 \mathrm{~\mu m} $ | 0.08 |
|
| A4. 7 DG3: $ q_1 = 78.5 \pm 5.5 \mathrm{~mm^{-1}} $ | 0.08 |
|
| A4. 8 DG3: $a = 78.8 \pm 5.2 \mathrm{~\mu m} $ | 0.08 |
|
| A4. 9 DG4: $ q_1 = 78.5 \pm 5.5 \mathrm{~mm^{-1}} $ | 0.08 |
|
| A4. 10 DG4: $a = 78.8 \pm 5.2 \mathrm{~\mu m} $ | 0.08 |
|
| A4. 11 DG5: $ q_1 = 78.5 \pm 5.5 \mathrm{~mm^{-1}} $ | 0.08 |
|
| A4. 12 DG5: $a = 78.8 \pm 5.2 \mathrm{~\mu m} $ | 0.08 |
|
|
A5. 1
Equation to find $b/a$:
$$ \cos (\pi b /a) = \sqrt{\frac{I(2)}{I(1)}}. $$ Equation which uses another reflexes are also possible. Another solutions are possible. |
0.40 |
|
| A5. 2 Measured intensities for two reflexes. | 0.20 |
|
| A5. 3 DG3: $a/b \in [7; 10]$ | 0.30 |
|
| A5. 4 DG4: $a/b \in [3.2; 4.8]$ | 0.30 |
|
| A5. 5 DG5: $a/b =[1.5; 2.5]$ | 0.30 |
|
| A6. 1 $\rho(x) = \begin{cases} 1, & x \in [0,b) \\ 0, & x \in [b, a) \end{cases} $ | 0.10 |
|
| A6. 2 Correct initial integral | 0.10 |
|
| A6. 3 Correct integration | 0.20 |
|
|
A6. 4
Final answer
$F_A(h) = 2 \cdot \frac{\sin \left( \pi h/p \right)}{q_1 h} \cdot e^{i \pi h/p } = \begin{cases} \frac{2\pi}{q_1} \cdot \left(\frac{1}{p} \right) , & h = 0 \\ F_1(h), & h \neq 0 \end{cases}$ |
0.20 |
|
| A6. 5 $h = \pm pm, \quad m \in \mathbb{N}$ | 0.10 |
|
| A7. 2 Correct initial integral or idea to subtract. | 0.20 |
|
|
A7. 3
Correct answer for $h = 0$
$F_B(0) = \frac{2\pi}{q_1} \cdot \left( 1 - \frac{1}{p} \right)$ |
0.20 |
|
|
A7. 4
Correct answer for $h\ne0$
$F_B(h) = 2 \cdot \frac{\sin \left( \pi h \right)}{q_1 h} \cdot e^{i \pi h} - 2 \cdot \frac{\sin \left( \pi h/p \right)}{q_1 h} \cdot e^{i \pi h/p } = \begin{cases} \frac{2\pi}{q_1} \cdot \left( 1 - \frac{1}{p} \right) , & h = 0 \\ - F_1(h), & h \neq 0 \end{cases}$ |
0.20 |
|
| A7. 5 $h = \pm pm, \quad m \in \mathbb{N}$ | 0.10 |
|
|
A8. 1
$\frac{I_{A, h=0}}{I_{B,h=0}} = \left( \frac{b}{a-b} \right)^2 = \left( \frac{1}{p-1} \right)^2$
or $\frac{I_{A, h=0}}{I_{B,h=0}} = \left( \frac{b}{a-b} \right) = \left( \frac{1}{p-1} \right)$ |
0.10 |
|
| A8. 2 $\frac{I_{A, h=0}}{I_{B,h=0}} = \left( \frac{b}{a-b} \right)^2 = \left( \frac{1}{p-1} \right)^2$ | 0.10 |
|
| A8. 3 $\frac{I_{A, h=1}}{I_{B,h=1}} = 1$ | 0.20 |
|
| B1. 1 $|\vec{q}| \sim \frac{2\pi}{a}$ | 0.20 |
|
|
B1. 2
Answer for the first vector
$|\vec{q}_1| = \frac{2\pi}{a_1 \sin \alpha}, \quad |\vec{q}_1| = \frac{2\pi}{a_2 \sin \alpha}$ |
0.30 |
|
|
B1. 3
Answer for the second vector
$|\vec{q}_2| = \frac{2\pi}{a_2 \sin \alpha}, \quad |\vec{q}_2| = \frac{2\pi}{a_1 \sin \alpha}$ |
0.30 |
|
| B1. 5 $\beta = \alpha$ | 0.20 |
|
|
B2. 1
Initial integral (it's for opposite unit cell, but for $h\ne0, k\ne0$ it doesn't matter) $$F(h, k) = \int_0^b \int_0^b e^{i q_x x} e^{i q_y y} dx dy$$.
Could be slightly different for two reasons: -another origin of axis; -one could use precise integral to direct unit cell |
0.20 |
|
| B2. 2 Correct integration (but may be final answer is not ok) | 0.10 |
|
| B2. 3 $|F(h, k)| = \frac{a^2}{\pi^2} \cdot \left| \frac{\sin (\pi h b/a)}{h} \cdot \frac{\sin (\pi k b/a)}{k} \right|, \quad h\neq0, \quad k\neq0$ | 0.20 |
|
|
B2. 4
Correct initial integral OR idea that 2nd atom is shifted:
$F_2(h, k) = F_A(h,k) \cdot e^{i q_x a/2} e^{i q_y a/2}$ |
0.20 |
|
| B2. 5 Correct integration (but may be final answer is not ok) | 0.10 |
|
| B2. 6 $|F(h, k)| = \frac{a^2}{\pi^2} \cdot \left| \frac{\sin (\pi h b/a)}{h} \cdot \frac{\sin (\pi k b/a)}{k} \cdot (1+(-1)^{h+k}) \right|, \quad h\neq0, \quad k\neq0$ | 0.20 |
|
| B3. 1 $a_{UC1} = 29.5 \pm 2.0~\mathrm{\mu m}$ | 0.15 |
|
| B3. 2 $a_{UC2} = 19.7 \pm 1.3~\mathrm{\mu m}$ | 0.15 |
|
| B3. 3 $a_{UC3} = 19.7 \pm 1.3~\mathrm{\mu m}$ or $a_{UC3} = 13.9 \pm 1.0~\mathrm{\mu m}$ | 0.15 |
|
| B3. 4 $a_{UC4} = 29.5 \pm 2.0~\mathrm{\mu m}$ | 0.15 |
|
|
B4. 2
1-B 2-A 3-D 4-C
(Enter integer number – number of right matches) |
4 × 0.10 |
|
|
B5. 2
Correct equation to solve. Smth like this:
$$ \cos (\pi b /a) = \sqrt{\frac{I(2)}{I(1)}}. $$ |
0.20 |
|
| B5. 3 Two measured intensities | 0.20 |
|
| B5. 4 Correct root of equation | 0.20 |
|
| B5. 5 $b = 10 \pm 2\mu m$ | 0.20 |
|
|
B6. 1
UC5: The first one of
$a_1= 19.7 \pm 1.8~\mathrm{\mu m}$, $a_2 = 39.4\pm 3.5~\mathrm{\mu m}$ |
0.15 |
|
|
B6. 2
UC5: The second one of
$a_1= 19.7 \pm 1.8~\mathrm{\mu m}$, $a_2 = 39.4\pm 3.5~\mathrm{\mu m}$ |
0.15 |
|
| B6. 3 UC5: $\alpha = 90 ^\circ$ | 0.10 |
|
|
B6. 4
UC6: The first one of
$a_1= 35.5 \pm 3.2~\mathrm{\mu m}$, $a_2 = 22.1 \pm 2.0~\mathrm{\mu m}$ (see also another in solution http://pho.rs/p/115/s) |
0.15 |
|
|
B6. 5
UC6: The second one of
$a_1= 35.5 \pm 3.2~\mathrm{\mu m}$, $a_2 = 22.1 \pm 2.0~\mathrm{\mu m}$ |
0.15 |
|
| B6. 6 UC6: $\alpha = (63 \pm 6) ^\circ$ | 0.10 |
|
|
B6. 8
UC7: The first one of
$a_1= 39.4 \pm 3.5~\mathrm{\mu m}$, $a_2= 35.4 \pm 3.2~\mathrm{\mu m}$ (see also another in solution http://pho.rs/p/115/s) |
0.15 |
|
|
B6. 9
UC7: The second one of
$a_1= 39.4 \pm 3.5~\mathrm{\mu m}$, $a_2= 35.4 \pm 3.2~\mathrm{\mu m}$ |
0.15 |
|
| B6. 10 UC7: $\alpha = (56 \pm 6) ^\circ$ | 0.10 |
|
| C1. 1 $h = 0$, $k = 0$ | 0.10 |
|
| C1. 2 $m = 1,~2,~4$ | 0.10 |
|
C1. 3
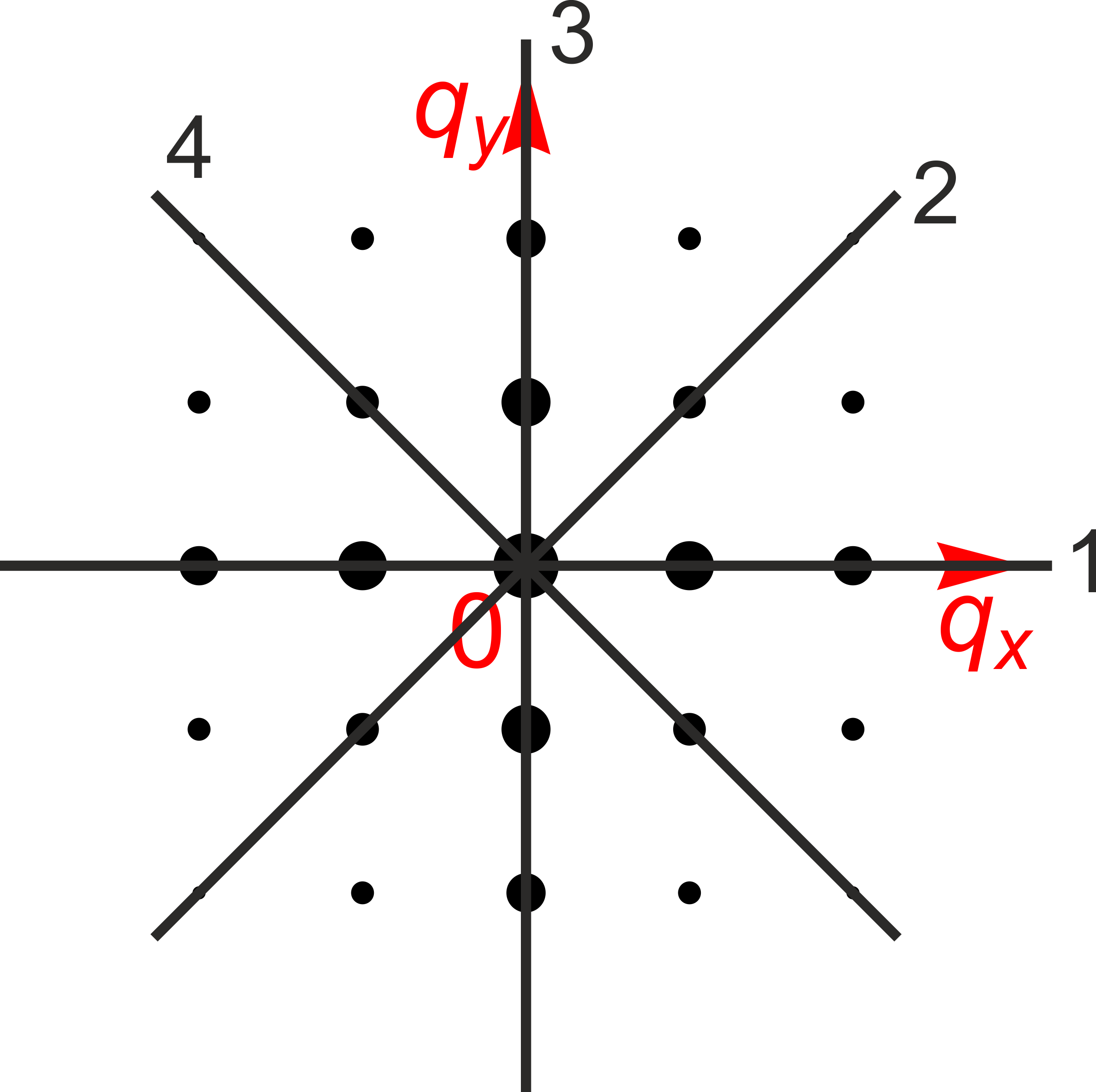
|
0.10 |
|
| C2. 1 1: $q_y = 0$ | 0.05 |
|
| C2. 2 2: $q_y = q_x$ | 0.05 |
|
| C2. 3 3: $q_x = 0$ | 0.05 |
|
| C2. 4 4: $q_x = -q_y$ | 0.05 |
|
| C3. 1 $C_1$: $I(q_x, q_y) = I(q_x, q_y)$ | 0.05 |
|
| C3. 2 $C_2$: $I(q_x, q_y) = I(-q_x, -q_y)$ | 0.05 |
|
| C3. 3 $C_4$: $I(q_x, q_y) = I(-q_y, q_x)$ or $I(q_x, q_y) = I(q_y, -q_x)$ | 0.10 |
|
| C3. 4 $q_y=0$: $I(q_x, q_y) = I(q_x, -q_y)$ | 0.05 |
|
| C3. 5 $q_x=0$: $I(q_x, q_y) = I(-q_x, q_y)$ | 0.05 |
|
| C3. 6 $q_x=q_y$: $I(q_x, q_y) = I(q_y, q_x)$ | 0.05 |
|
| C3. 7 $q_x=-q_y$: $I(q_x, q_y) = I(-q_y, -q_x)$ | 0.05 |
|
| C4. 1 $I(-h, -k) = I(h, k)$ | 0.10 |
|
| C4. 2 Corresponds to $C_2$ | 0.10 |
|
| C5. 1 $ f_2 (q_x, q_y) = F(-q_x, q_y)$ | 0.10 |
|
| C5. 2 $ f_3 (q_x, q_y) = F(q_y, q_x)$ | 0.10 |
|
| C5. 3 $ f_4 (q_x, q_y) = F(q_x, q_y) \cdot e^{i(q_x x_1+q_y y_1)}$ | 0.20 |
|
| C6. 1 Explanation | 0.30 |
|
| C6. 2 $C_1$, $C_2$, $C_3$, $C_4$, $C_6$ | 0.20 |
|
C7. 1
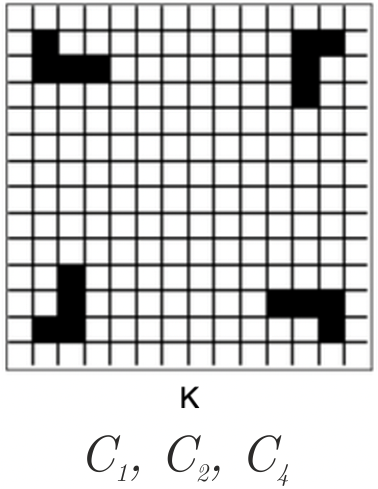
|
0.10 |
|
C7. 2
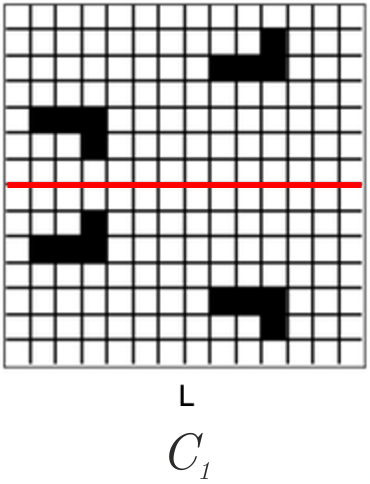
|
0.10 |
|
C7. 3
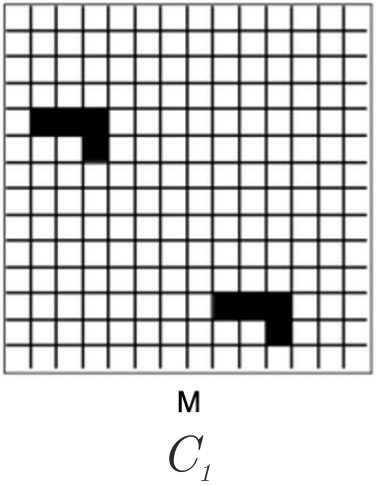
|
0.10 |
|
C7. 4
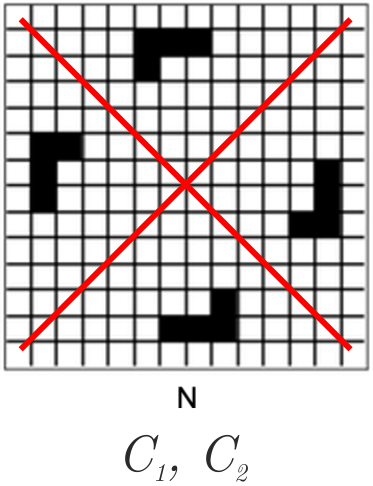
|
0.10 |
|
C7. 5

|
0.10 |
|
C7. 6
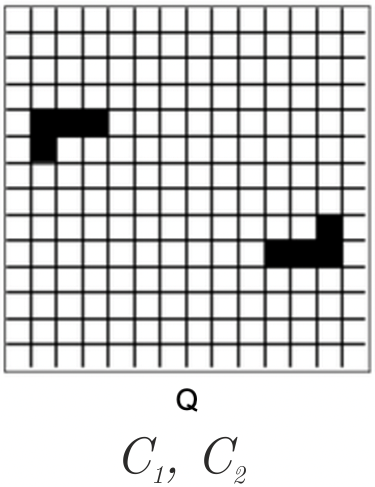
|
0.10 |
|
C7. 7
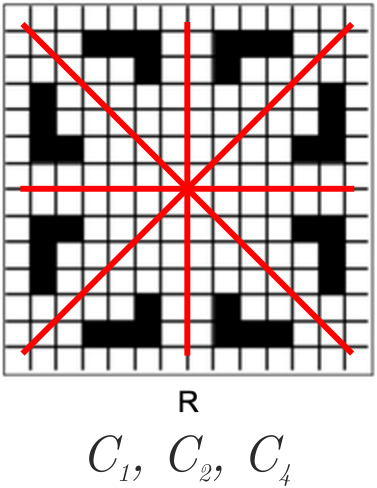
|
0.10 |
|
C7. 8

|
0.10 |
|
C7. 9
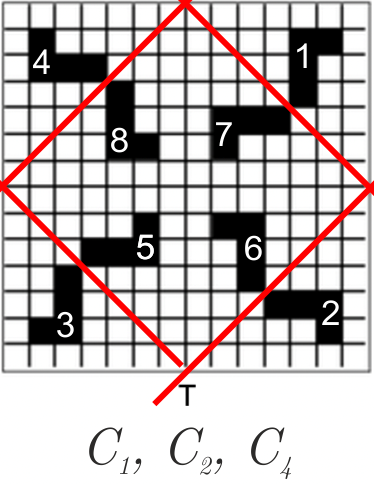
|
0.10 |
|
| C7. 10 If symmetry $C_1$ is not presented | -0.10 |
|
C8. 1

|
0.10 |
|
C8. 2

|
0.10 |
|
C8. 3

|
0.10 |
|
C8. 4

|
0.10 |
|
| C8. 5 1-L, 2-M, 5-N, 8-K | 4 × 0.10 |
|
| C9. 1 $\{4, 6\}$ corresponds to $\{R, T\}$, $\{3, 7, 9\}$ to $\{P, Q, S\}$. | 0.25 |
|
| C9. 2 3-P, 4-R, 6-T, 7-Q, 9-S. (Enter integer number – number of right matches) | 5 × 0.15 |
|
| C10. 1 Answer - NO | 0.10 |
|
| C10. 2 Explanation – structure has $C_5$ symmetry. | 0.20 |
|
|
D1. 1
Electric field of the reflex $\vec{q} = 0$ is proportional to transparent area of an unit cell and should be $E_0$
$$ E = \frac{N_{transparent}}{N_{all}} E_0. $$ |
0.20 |
|
| D1. 2 $E_{MR0} = \left( \frac{5}{16} \right) \cdot E_0$ | 0.30 |
|
| D1. 3 $I_{MR0} = \left( \frac{5}{16} \right)^2 \cdot I_0$ | 0.10 |
|
| D1. 4 $E_{MR2} = \left( \frac{7}{16} \right) \cdot E_0$ | 0.30 |
|
| D1. 5 $I_{MR2} = \left( \frac{7}{16} \right)^2 \cdot I_0$ | 0.10 |
|
| D2. 1 Measurements. (Enter integer number – number of right points) | 25 × 0.02 |
|
|
D2. 2
\begin{equation}
\rho(\chi, \gamma) = \sum_{h=-2}^{2} \sum_{k=-2}^{2} \sqrt{I(h, k)} \cdot \cos \left( \varphi(h, k) - \frac{\pi}{2} (\chi h + \gamma k) \right). \end{equation} |
0.50 |
|
| D2. 3 Calculations | 0.50 |
|
| D2. 4 Structure X | 0.50 |
|
| D3. 1 Measurements. (Enter integer number – number of right points) | 25 × 0.02 |
|
| D3. 2 Calculations for each black square. (Enter integer number – number of right points) | 11 × 0.10 |
|
| D3. 3 Answer | 0.40 |
|