6★ Мальчик бежит по со скоростью $v = 5~м/с$ по ледяной поверхности большого замёрзшего озера в направлении на север. Коэффициент трения между его обувью и льдом равен $\mu = 0.1$. Для упрощения примем, что сила реакции между мальчиком и льдом, которая вообще говоря может меняться во время движения, постоянна.
15 Маленькое тело может скользить вниз из точки $A$ в точку $B$ по одной из двух искривлённых поверхностей, имеющих поперечную форму как показано на рисунке. Эти кривые являются дугами окружностей, лежащими симметрично относительно прямой, соединяющей $A$ и $B$. На протяжении всего движения по каждой из траекторий, тело не покидает кривой.

16 В безветренный день велосипедист может подниматься в гору с максимальной скоростью $v_1 = 12~км/ч$, а спускаться по тому же склону с максимальной скоростью $v_2 = 36~км/ч$. С какой максимальной скоростью (т.е. прикладывая максимальное усилие) велосипедист может ехать по прямой дороге, если максимальное усилие, не зависит от скорости, с которой едет велосипедист?
В этой задаче понятие «усилие» может толковаться по-разному и означать либо
Решите задачу для обоих толкований.
17★ Анна и Боб решили устроить гонку на велосипедах, скатываясь на свободном ходу с очень длинного склона, составляющего угол $\theta$ с горизонтом. Они оба имеют одинаковую модель велосипеда и никто из них не крутил педали во время спуска. Суммарная масса Анны и её велосипеда равна $m_A = 60~кг$, масса Боба и его велосипеда равна $m_B = 110~кг$. Из-за избыточного веса Боба сила сопротивления воздуха, действующая на него, в полтора раза больше, чем на Анну при одинаковой скорости движения.
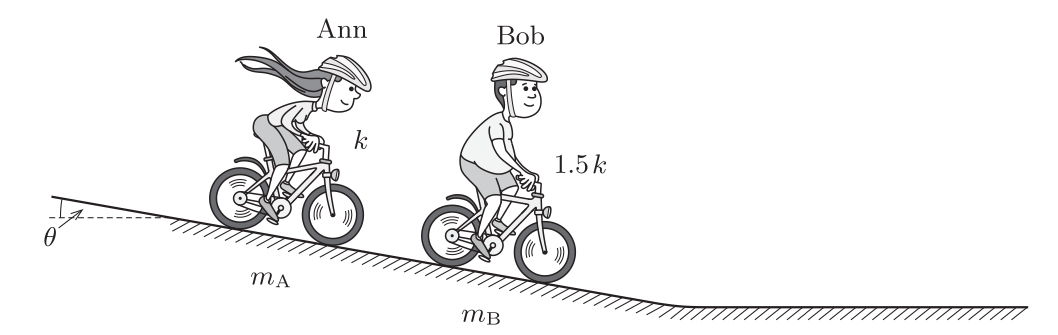
Считать, что их замедление обусловлено сопротивлением воздуха (пропорциональным квадрату скорости), трением в подшипниках ступицы и трением качения. Последние два эффекта следует рассматривать как обычное трение скольжение с «эффективным коэффициентом трения» $\mu$.
19★ На маленькую жемчужину, движущийся глубоко под водой, действует сила вязкого трения, пропорциональная его скорости (закон Стокса). Если её отпустить под водой, то через некоторое время она будет падать с установившейся скоростью $v_1$. Точно такой же жемчужине сообщают под водой горизонтальную скорость $v_2$.
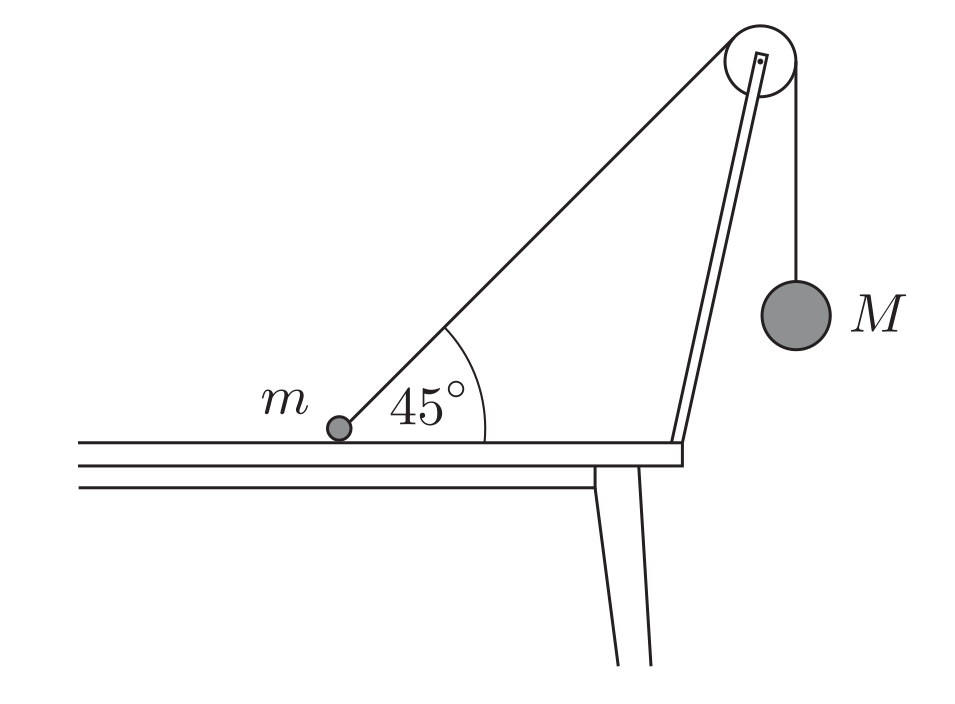
20 Два сферических тела массы $m$ и $M$ соединены тонкой нитью, проходящей через прикреплённый к столу блок пренебрежимо малой массы. В начальный момент времени они удерживаются в положении, показанном на рисунке, затем их одновременно отпускают. Масса $M$ во много раз (скажем, в тысячу) больше массы $m$. Трение между маленьким шариком и поверхностью стола пренебрежимо мало.
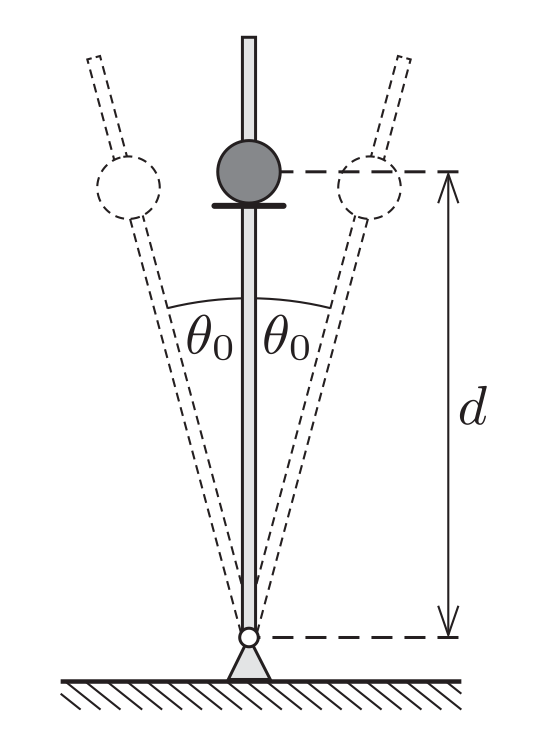
21★ Маленькая гладкая бусинка надета на жёсткий, гладкий, вертикальный стержень, который может вращаться вокруг своего конца. Изначально бусинка покоилась на маленьком диске, прикреплённом к стержню на расстоянии $d$ от оси вращения. Стержень начинает совершать гармонические колебания вокруг своего изначального положения с маленькой угловой амплитудой $\theta_0$ (смотри рисунок).
22★★ На вершину поверхности доски длины $L = 6~м$, расположенной под углом $\alpha = 10^{\circ}$ к горизонту, положили небольшой брусок. Доска начинается совершать гармонические колебания в направлении, параллельном прямой спуска, с амплитудой $A = 1~мм$ и с угловой частотой $\omega = 500~{рад/с}$. Коэффициенты трения покоя и скольжения между бруском и доской совпадают и равны $\mu = 0.4$.

24★ Скалолаз (в прошлом цирковой артист) хочет провести ночь, провисев на горе в положении, как показано на рисунке. Для этого он закрепил себя к поверхности скалы с помощью четырёх необычных гибких пружин. Массы и начальные длины этих пружин пренебрежимо малы, а их коэффициенты жёсткости равны $k_1 = 150~Н/м$, $k_2 = 250~Н/м$, $k_3 = 300~Н/м$, $k_4 = 400~Н/м$. Для простоты, скалолаз можно считать точечным с массой $m = 70~кг$.

27★ Два постоянных магнита расположены на горизонтальном, очень скользком столе. Длина промежутка между ними равно $d$, а расстояние между их центрами масс равно $d + d_0$. Магниты находятся в таком положении, что они притягиваются друг к другу, а моменты сил, которые бы вращали их, отсутствуют.
Если удерживать один магнит, а второй отпустить, то они столкнутся через $0.6~с$. Если сделать наоборот, удерживать второй, а отпустить первый, то столкнутся они через $0.8~с$.

37★ Из-за сопротивления воздуха оставленные на орбите искусственные спутники к концу срока службы начинают терять энергию в верхних слоях атмосферы, прежде чем окончательно сгореть, достигнув более плотных нижних слоёв. Можно показать, что спутник, изначально двигавшийся по круговой траектории, будет продолжать двигаться по круговой орбите с медленно уменьшающимся радиусом.
Оставленный спутник весом в полтонны вращается вокруг Земли по примерно круговой орбите. Действующая на него сила сопротивления может быть выражена как $c{\rho}v^2$, где $c = 0.23~м^2$, $\rho$ — плотность воздуха на высоте, на которой находится спутник, $v$ - его скорость.

38★★ Хорошо известно, что Луна всегда более или менее обращена к Земле одной и той же стороной. Данный факт - не совпадение, а прямое следствие приливных сил, действующих между Землей и Луной. Со временем приливные силы непрерывно замедляли вращение Луны вокруг собственной оси, пока период этого вращения не стал равным периоду обращения Луны вокруг Земли. По той же причине вращение Земли вокруг собственной оси постоянно замедляется, а орбитальная скорость Луны уменьшается.
Считать, что орбита Луны остаётся круговой, а приливными силами Солнца можно пренебречь.
40★ Для подготовки к межзвёздному путешествию была предложена идея, как можно компенсировать отсутствие гравитации. Было предложено сделать космический корабль в форме длинного и тяжелого цилиндра диаметра $2R = 20~м$ и равномерно вращать его вокруг своей оси с таким периодом, чтобы на его поверхности космонавты ощущали земное ускорение свободного падения $g = 10~м/с^2$.
Во время путешествия космонавты тренируются в тренажёрном зале, высотой (с потолками высоты) $5~м$, «полом» которого является поверхность цилиндра. Во время тренировок космонавты замечают, что все не совсем так, как на Земле.
45★ Очень густой туман состоит из большого числа капелек, двигающихся с пренебрежимо малой скоростью. Если одна из капель начинает падать, то она будет поглощать все маленькие капли на своём пути (см. рисунок). Оказалось, что эта растущая капля (которую можно считать сферической) падает с постоянным ускорением даже несмотря на наличие силы сопротивления воздуха, пропорциональной площади капли, а также квадрату её скорости.

130 Три маленькие положительно заряженные бусинки удерживаются по одной в вершинах треугольника. Их массы равны $m_1$, $m_2$, $m_3$, а заряды $Q_1$, $Q_2$, $Q_3$, соответственно. Когда бусинки отпускают из состояния покоя, они начинают двигаться по разным прямолинейным траекториям. Движение происходит в вакууме, гравитацией можно пренебречь.
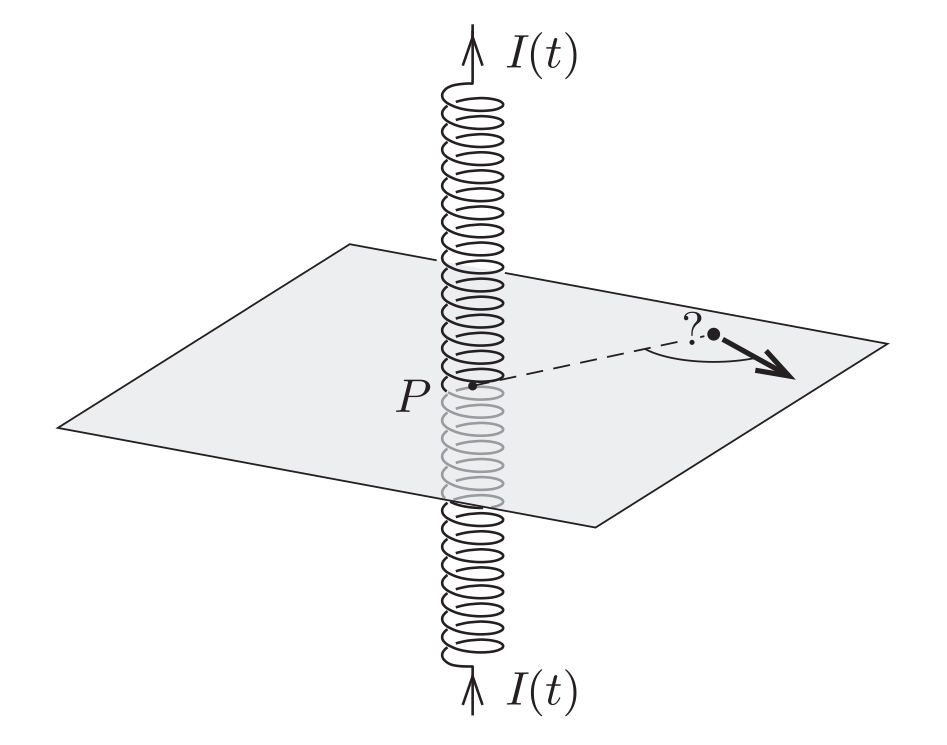
164★ Две одинаковые петли с током $I$ расположены в параллельных плоскостях. Их центры лежат на одной нормали к обеим плоскостям (см. рисунок). Из точки $O$ пересечения общей нормали с плоскостью, параллельной и равноудалённой от плоскостей петель, стартует с начальной скоростью $v_0$, лежащей в этой же плоскости.

165★ Заряженная частица входит в область, в которой сила вязкого трения, действующая на неё, пропорциональна её скорости и останавливается на расстоянии $10~см$ от точки входа в область. Если повторить данное движение, предварительно создав в этой области однородное магнитное поле, то частица остановится на расстоянии $6~см$ от точки входа.

166★ Небольшой шарик массы $m$ имеет положительный заряд $q$ и подвешен на непроводящей нити длины $l$. Получившийся маятник помещают в однородное магнитное поле $B$. Эксперимент показывает, что если в начальный момент времени немного отклонить шарик, то он начнёт колебательное движение в медленно вращающейся вертикальной плоскости.
167★★ В данной задаче исследуется движение двух электронов в плоскости, перпендикулярной линиям однородного магнитного поля $B$.
177 Длинный, прямой провод пренебрежимо малого сопротивление изогнут в V - образную форму, так что два его плеча образуют угол $\alpha$ друг с другом. Провод помещают в однородное магнитное поле $B$, перпендикулярное его плоскости. На него, на расстоянии $x_0$ от его вершины $A$ кладут стержень массы $m$, имеющий сопротивление $r$ на единицу длины, так что он перпендикулярен биссектрисе угла $\alpha$ (см. рисунок).

В начальный момент времени стержню сообщают скорость $v_0$, направленную от вершины $A$ по биссектрисе угла $\alpha$. Стержень достаточно длинный, чтобы не упасть с провода в течение всего последующего движения, а электрический контакт между ними хороший — даже несмотря на то, что трение между ними пренебрежимо мало.
186★ Маленькая заряженная бусинка, изначально находившаяся в состоянии покоя, может двигаться по горизонтальной, гладкой плоскости. Недалеко от бусинки расположен длинный, вертикальный соленоид, в котором ток сначала равномерно увеличивается от нуля до какого-то заданного значения, а затем также равномерно уменьшается обратно до нуля.