
177 Длинный, прямой провод пренебрежимо малого сопротивление изогнут в V - образную форму, так что два его плеча образуют угол $\alpha$ друг с другом. Провод помещают в однородное магнитное поле $B$, перпендикулярное его плоскости. На него, на расстоянии $x_0$ от его вершины $A$ кладут стержень массы $m$, имеющий сопротивление $r$ на единицу длины, так что он перпендикулярен биссектрисе угла $\alpha$ (см. рисунок).

В начальный момент времени стержню сообщают скорость $v_0$, направленную от вершины $A$ по биссектрисе угла $\alpha$. Стержень достаточно длинный, чтобы не упасть с провода в течение всего последующего движения, а электрический контакт между ними хороший — даже несмотря на то, что трение между ними пренебрежимо мало.
178 Внутри вертикальной, тонкостенной, неферромагнитной (скажем, латунной) трубки очень медленно падает довольно большой, цилиндрический постоянный магнит. Чтобы пройти расстояние между двумя некоторыми маркерами требуется время $t_1$. Если эксперимент повторяется с другой также неферромагнитной (скажем, медной) трубкой той же длины, но немного большего диаметра, то то же самое расстояние магнит пройдёт за время $t_2$.
180★ Замкнутый круговой виток радиуса $r$ состоит из провода с сопротивлением $R$ и идеального диода. Виток лежит в горизонтальной плоскости, а сквозь его центр проходит длинная, вертикальная стеклянная труба (см. рисунок).

181★ Три почти полные круглые петли, имеющие радиусы $R$, $2R$ и $4R$, изготовленные из тонкой проволоки, концентрически расположены на горизонтальном столе, как показано на рисунке. К средней петле подаётся изменяющийся со временем ток.

182
184★ Три одинаковые, “широкие” электромагнитные катушки с незначительным омическим сопротивлением равномерно намотаны на “узкий” тороидальный железный сердечник, как показано на рисунке. К первой катушке подключают (идеальный) генератор переменного тока, ко второй - разомкнутый выключатель $S$, к третьей - вольтметр с очень большим сопротивлением. В таком подключении вольтметр показывает среднеквадратичное значение напряжения, равное половине среднеквадратичного значения напряжения на источнике.
Теперь переключатель $S$ замыкается, заворачивая клеммы второй катушки.

185★★ Две идеальные (с нулевым омическим сопротивлением) катушки намотаны на одинаковые тороидальные, воздушные сердечники. Катушки имеют разное число витков $N_1$ и $N_2$, а сами сердечники связаны, как показано на рисунке, причём их плоскости перпендикулярны друг другу. К катушке с числом витков $N_1$ подключают источник переменного напряжения со среднеквадратичным значением напряжения, равным $V_0$, а к другой катушке подсоединяется идеальный вольтметр.

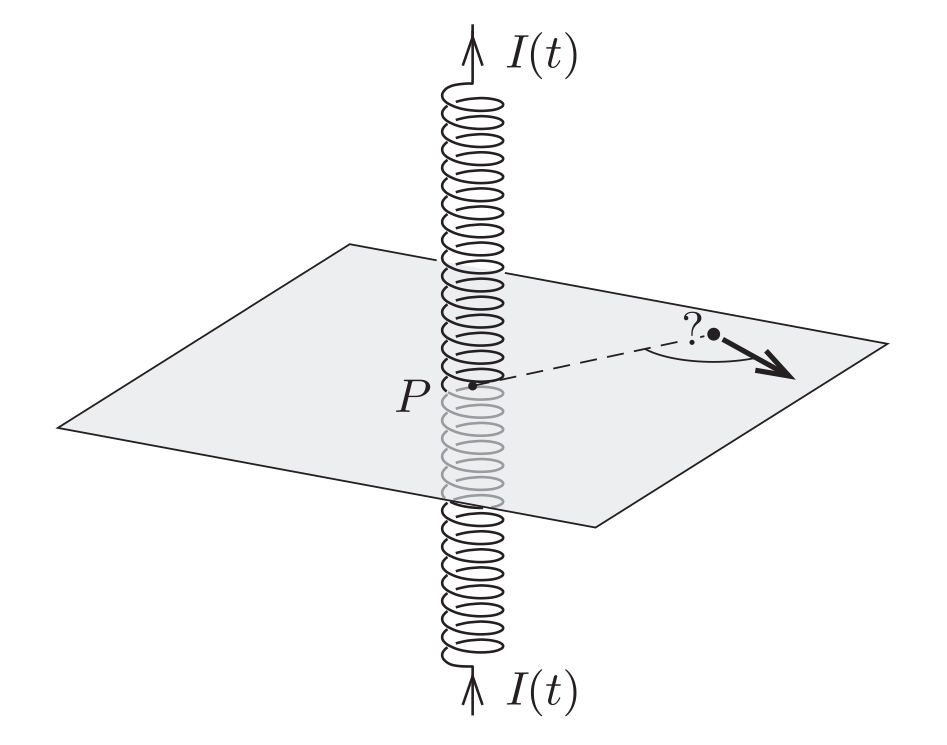
186★ Маленькая заряженная бусинка, изначально находившаяся в состоянии покоя, может двигаться по горизонтальной, гладкой плоскости. Недалеко от бусинки расположен длинный, вертикальный соленоид, в котором ток сначала равномерно увеличивается от нуля до какого-то заданного значения, а затем также равномерно уменьшается обратно до нуля.
188★ Цилиндрический конденсатор с внешним и внутренним радиусами, равными $R$ и $R - d$ ($d \ll R$) соответственно, высотой $l$ и массой $M$ подвешен на непроводящих шнурах в области вертикального, однородного, магнитного поля $B$. Конденсатор может свободно вращаться (как единое целое) вокруг своей вертикальной оси симметрии, но не может перемещаться по горизонтали. В начальный момент времени конденсатор заряжен, а напряжение между его обкладками равно $V$.

Что произойдёт, если:
190★★ Плоский конденсатор с вертикальными пластинами заряжают как показано на рисунке, и помещают нижними краями выше и по обе стороны от небольшой горизонтальной стрелки компаса. Вершины пластин соединяют с помощью небольшого проводящего стержня и он начинает разряжаться.
Опишите реакцию стрелки компаса на процесс разрядки.

Задача была предложена участникам Венгерской национальной олимпиады по физике несколько лет назад. «Официальное» решение задачи выглядит примерно так.
Когда вершины пластин соединяются проводящим стержнем, по нему слева направо начинает протекать электрический ток $I = -dQ/dt$. В то же время электрическое поле между пластинами $E = {\varepsilon_0}^{-1}Q/A$ меняется, из-за чего, согласно одному из уравнений Дж. К. Максвелла, возникает так называемый ток смещения. Плотность этого тока смещения пропорциональна скорости изменения электрического поля с коэффициентом пропорциональности $\varepsilon_0$. Таким образом
\begin{equation}
j_D = \varepsilon_0\dot{E} = \frac{1}{A}\frac{dQ}{dt} = -\frac{I}{A}.
\end{equation}
Ток в стержне (равный $I$) и ток смещения (равный $j_DA = -I$) взятые вместе могут быть рассмотрены как замкнутый контур с током.
Согласно уравнениям Максвелла, магнитные поля создаются не только обычными электрическими токами, но и токами смещения. Поскольку ток смещения и ток в стержне имеют равные величины (но противоположные направления), а ток смещения ближе к стрелке компаса, его эффект больше. Вот почему во время процесса разрядки стрелка компаса имеет тенденцию вращаться (см. рисунок ниже), при этом ее северный полюс движется в направлении против часовой стрелки (от показанного положения), если смотреть сверху. Впоследствии он вернется в исходное положение.
