1 Три маленькие улитки в исходном положении находятся в вершинах равностороннего треугольника со стороной $a = 60 ~см$. В некоторый момент времени все приходит в движение: первая улитка движется ко второй, вторая - к третьей, третья - к первой с одинаковыми и постоянными по величине скоростями $v = 5~ см/мин$. Во время движения каждая улитка всегда оказывается впереди по отношению к соответствующей следующей улитке.

a Сколько пройдет времени и какой путь пройдут улитки до того, как они встретятся?

A H

b Каковы уравнения их траекторий?

A

c Если улитки считать точечными, то сколько раз каждая улитка повернется вокруг точки их встречи?

A

3 Лодка может плыть в стоячей воде со скоростью $v= 3~ м/с$. Лодочник хочет переплыть реку постоянной ширины по самому короткому пути.

a В каком направлении по отношению к берегу он должен грести, если скорость $u$ воды в реке равна $u = 2~м/с$?

A H

b В каком направлении по отношению к берегу он должен грести, если скорость $u$ воды в реке равна $u =4~м/с$?

A H

Считайте, что скорость воды в реке везде одинакова.

5 Четыре черепашки движутся равномерно и прямолинейно по очень большой плоской поверхности. Направления их траекторий произвольны (но не параллельны, т.е. любые две черепашки могли бы встретиться), при этом пересечься в какой-либо точке могут не более двух траекторий. На текущий момент произошли уже пять встреч из $(4 \times 3)/2 = 6$ возможных.

Можно ли тогда с определенностью сказать, что шестая встреча тоже произойдет?

A H

36 Минутная стрелка церковных часов вдвое длиннее, чем часовая. В какой момент после полуночи конец минутной стрелки будет удаляться от конца часовой стрелки с наибольшей скоростью?

A H

37 Под каким углом к горизонту нужно бросить камень, чтобы он при движении все время удалялся от бросающего?

A H

38^★ Ствол дерева диаметром $D = 20~ см$ лежит на горизонтальной земле. Ленивый кузнечик хочет перепрыгнуть через ствол. Найдите минимальную скорость прыжка кузнечика, чтобы он смог осуществить свой замысел. Сопротивление воздуха не учитывать.

A H

40 Фонтан состоит из маленького полусферического распылителя, который находится на поверхности воды в бассейне, как показано на рисунке. Распылитель имеет множество равномерно распределенных маленьких отверстий, через которые вода вытекает с одинаковой скоростью во всех направлениях.

Какова форма водяного «колокола», сформированного струями?

A H

41 Частица массой $m$, имеющая электрический заряд $Q$, находится под воздействием однородного поля тяжести и однородного горизонтального электрического поля напряженностью $E$. Частица начинает движение со скоростью $v$ под углом $\theta$ к горизонту в вертикальной плоскости, параллельной электрическому полю.

На какое максимальное расстояние может переместиться частица вдоль исходной горизонтали?

A H

64 Голодный паук приготовился поймать насекомое, если оно окажется в паутинке, которая натянута между ним и стеной. Длина нити $1~ м$. На нить попала гусеница (см. рис). Увидев паука, она стала уползать от него к стене со скоростью $v_г = 1~мм/с$ относительно нити, а паук, оставаясь на месте, стал вытягивать свой конец нити со скоростью $v_0 = 1~см/с$, считая, что нить может растягиваться без ограничений.

Доползет ли гусеница до стены?

A H

65^★ Голодный паук приготовился поймать насекомое, если оно окажется в паутинке, которая натянута между ним и стеной. Длина нити $1~ м$. На нить попала гусеница (см. рис). Увидев паука, она стала уползать от него к стене со скоростью $v_г = 1~мм/с$ относительно нити, паук не сидит на месте, а удаляется от стены, увлекая за собой конец нити и стал вытягивать свой конец нити со скоростью $v_0 = 1~см/с$, считая, что нить может растягиваться без ограничений.

Доползет ли гусеница до стены?

A H

a Можно ли расположить гвозди так, чтобы шарик перелетел из точки $A$ в точку $B$ быстрее, чем если бы он скользил без трения вниз по кратчайшему расстоянию, т.е. по прямой линии $AB$;

A H

b Можно ли расположить гвозди так, чтобы шарик достиг точки $B$ за время $t < 0.4 ~с$?

A

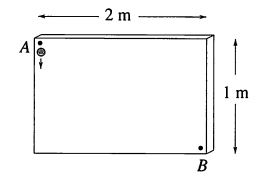
84^★ Лодочник отправляется из точки $A$ на одном берегу прямого канала и движется к другому берегу, держа курс всегда на точку $B$, противоположную точке отправления. Скорость воды в канале в любом месте равна $v$. Лодочник, работая веслами равномерно, обеспечивает такую скорость лодки, чтобы в отсутствие течения воды она была равна $v$.

a Как далеко от точки $B$ вниз по течению вода унесет лодку?

A H

b По какой траектории относительно берега плывет лодка?

A

86^★ На берегу находятся пункты $A$ и $B$, удаленные на расстояние $L$ друг от друга. Контрабандисты отправляются на судне в открытое море из пункта $A$ перпендикулярно берегу с постоянной скоростью $v$. Офицер береговой охраны, обнаружив нарушителей с помощью прибора ночного видения в момент отчаливания их судна, тотчас устремляется за ними в погоню на катере из точки $B$. Катер всегда держит курс на нарушителей и, перемещаясь с постоянной скоростью, настигает судно на расстоянии $L$ от берега.

Во сколько раз скорость катера береговой службы больше скорости судна контрабандистов?

A H