2 Маленький предмет покоится на краю горизонтального стола. Его толкают таким образом, что он падает с другой стороны стола, ширина которого $1~м$, через $2~с$. Имеет ли предмет колеса?

A H

a Найдите длину троса в нерастянутом состоянии.

A H

b Найдите максимальные скорость и ускорение, которые достигаются во время падения

A

8 Айсберг, выступающий над водной поверхностью на $10 ~м$, представляет собой вертикально расположенную правильную пирамиду. Пренебрегая любым вынужденным движением воды, найдите период малых колебаний айсберга по вертикали. Плотность льда $900 ~кг/м^3$.

A H

12 Маленький упругий шарик падает вертикально на плоскость, наклоненную под углом $\alpha$ к горизонту.

Верно ли, что расстояния между последовательными точками ударов шарика растут в арифметической прогрессии?

A H

Считайте, что столкновения абсолютно упругие, а сопротивление воздуха пренебрежимо мало.

Как должен бежать по платформе хомяк после освобождения колеса, чтобы оно не вращалось?

A H

24 Ведро с водой подвешено на веревке. Его отклоняют от положения равновесия и отпускают. В системе начинаются колебания. Однако ведро протекает, и уровень воды в нем уменьшается. Как изменится период колебаний, когда вся вода вытечет?

A H

32^★ Каким бы был мировой рекорд по прыжкам в высоту среди мужчин (на соревнованиях в закрытом помещении) на Луне?

A H

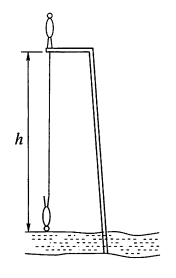
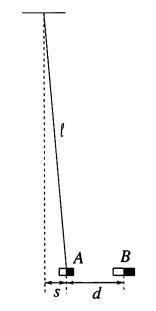
33 Маленький шарик $B$ лежит на краю стола высотой $1~ м$, другой такой же шарик $A$ подвешен на нити длиной $1 ~м$ и представляет собой математический маятник (см. рис). Если нить с шариком $A$ привести в горизонтальное положение и отпустить, то между шариками произойдет упругое столкновение. Рассматривая движение шарика $B$ только до момента его падения на землю, ответьте на вопросы:

a Какой шарик дольше находится в движении?

A H

b У какого шарика больше длина траектории?

A

34 Маленький груз закреплен на одном конце нити длиной $L = 50~ см$. Вследствие вынужденного движения другого конца нити груз движется с постоянной скоростью $v = 3.0 ~м/с$ в вертикальной плоскости по кругу радиусом $R = 50~ см$.

Начертите «траектории» обоих концов нити для промежутков кругового движения груза в $15^\circ$, указывая на каждой «траектории» положения концов нити в один и тот же момент времени.

A H

35 Точка $P$, расположена над наклонной плоскостью, соединяется отрезком прямого тонкого стержня с некоторой точкой $P'$ на наклонной плоскости. Маленькое кольцо может скользить по этому стержню без трения из точки $P$ в точку $P'$. Как должна быть выбрана точка $P'$, чтобы время движения кольца было минимальным?

A H

37 Под каким углом к горизонту нужно бросить камень, чтобы он при движении все время удалялся от бросающего?

A H

38^★ Ствол дерева диаметром $D = 20~ см$ лежит на горизонтальной земле. Ленивый кузнечик хочет перепрыгнуть через ствол. Найдите минимальную скорость прыжка кузнечика, чтобы он смог осуществить свой замысел. Сопротивление воздуха не учитывать.

A H

39^★ Прямая однородная тонкая соломинка покоится на гладкой доске. На каждом ее конце сидит по блохе.

Покажите, что если масса $M$ соломинки не слишком большая по сравнению с массой $m$ каждой из блох, то они могут одновременными прыжками с одинаковыми скоростью и углом взлета перепрыгнуть с одного конца соломинки на другой без столкновения друг с другом в воздухе.

A H

70^★ Цистерна, заполненная жидкостью, находится в покое на горизонтальном железнодорожном пути (см. рис). Снизу цистерны у левого края имеется вертикальная труба с краном.

a Как начнет двигаться цистерна, если открыть кран?

A H

b Как долго продолжится движение цистерны в этом направлении?

A

Считайте, что всякое трение отсутствует.

73^★ Большой кувшин и бочку с пивом поставили на платформу весов. Бочка находится выше кувшина. Кран в бочке открывают и начинают наливать пиво в кувшин. Как изменяются при этом показания весов?

A H

77 Нерастянутая легкая пружина закреплена своими концами в горизонтальном положении. Посередине пружины закреплён маленький шарик массой $m$ (см. рис). Шарик смещают поперек пружины на $1~ см$ и отпускают. Период поперечных колебаний шарика $T_1$ оказался равным $2~ с$.

Чему будет равен период колебаний $T_2$ , если начальное смещение будет $2 ~см$?

A H

Силу тяжести не учитывать и считать, что длина пружины много больше поперечных смещений шарика.

78^★ Один конец легкой слабой пружины в нерастянутом состоянии шарнирно закреплен в точке $O$, ко второму концу прикреплен шарик массой $m$. Шарик с пружиной приводят в горизонтальное положение и отпускают (см. рис).

Чему равна длина пружины в тот момент, когда она проходит вертикальное положение?

A H

Жесткость пружины $k$, длина свободной пружины $L$. Слабость пружины означает, что $mg\gg kL$.

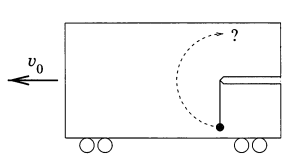
79^★ Тяжелое тело массой $m$ висит на гибкой нити в железнодорожном вагоне, который движется со скоростью $v_0$ на треке испытания безопасности поездов, как показано на рисунке. Сильным постоянным торможением вагон останавливают.

Может ли груз оказаться при этом в противоположном относительно точки подвеса положении при натянутой нити?

A H

80^★★ Стакан, частично заполненный водой, прикреплен к клину, который скользит без трения по склону горки (см. рис). Дно стакана горизонтально, так как углы наклона горки и клина одинаковы и равны $\alpha$ . Масса горки $M$, суммарная масса клина, стакана и воды $m$.

a Какой угол будет составлять поверхность воды с наклонной плоскостью если: а) горка неподвижна; б) горка может двигаться свободно в горизонтальном направлении?

A H

b Исследуйте также случай, когда $m\gg M$.

A

c А что случится, если при помощи ручки привести горку в колебательное движение, но так, чтобы клин не слетел с горки в ее высшей точке?

A

82 Мост в форме выпуклой параболы перекинут через реку шириной $100~м$ (см. рис). Самая высокая точка моста находится выше уровня берегов на $5 ~м$. Автомобиль массой $1000~кг$ движется по мосту с постоянной скоростью $20~м/с$.

Найдите силу, с которой автомобиль давит на мост, когда он: а) находится в самой высокой точке моста; б) прошел три четверти длины моста.

A H

Сопротивлением воздуха пренебречь и считать ускорение свободного падения $g = 10~ м/с^2$.

83 Материальная точка массой $0.5~кг$ перемещается с постоянной скоростью $5~м/с$ по эллиптическому треку. Когда точка находится на конце большой оси эллипса, на нее действует сила $10~Н$, когда на конце малой оси — всего лишь $1.25~Н$. Каковы длины осей эллипса?

A H

Какова будет конечная скорость мальчика, если сила трения не зависит от скорости, а сопротивление воздуха отсутствует?

A H

90 Малое тело массой $m$ и зарядом $q$ удерживают в покое на небольшом расстоянии $d$ от неподвижной металлической плоскости. Сколько времени потребуется, чтобы тело достигло плоскости, если его отпустить? Силу тяжести не учитывать.

A H

a Зависимость силы взаимодействия между магнитами от расстояния определяется выражением $F_м(x)=\pm K/x^n$, причём знак зависит от относительной ориентации полюсов магнитов. Используя данные задачи, найдите значение показателя степени $n$.

A H

b Магнит $B$ помещают на дно стеклянной трубки, расположенной вертикально и запаянной снизу. Сверху в трубку медленно опускают магнит $A$ в такой ориентации, что магниты отталкиваются друг от друга. Внутренний диаметр трубки чуть больше поперечных размеров магнитов и не позволяет им изменять свои ориентации. Найдите расстояние между магнитами в положении равновесия.

A

189^★ Изотоп $^7\mathrm{Be}$ — радиоактивный элемент с периодом полураспада 53.37 дней. Когда бериллий нагревают до температуры несколько тысяч градусов, его период полураспада изменяется. Как это можно объяснить?

A H

184^★ Точечное тело массой $m$ и зарядом $q$, удерживаемое в покое, находится в однородном поле тяготения и горизонтальном магнитном поле. По какой траектории будет двигаться тело, если его освободить?

A H

186^★ В вакуумной камере по тончайшему прямому проводу, который имеет очень высокую проводимость, течет ток $10~ А$. Электроны с начальной скоростью $v_0$ начинают двигаться перпендикулярно проводу от точки, которая находится на расстоянии $r_0$ от центра провода. Скорость электрона такова, что он не может оказаться на расстоянии меньше чем $r_0/2$. Чему равна скорость $v_0$? Влиянием геомагнитного поля пренебречь.

A H

193^★ Первоначально два позитрона и два протона удерживаются в вершинах квадрата так, что позитроны находятся на одной диагонали, а протоны - на другой (см. рис). Сторона квадрата $a = 1~ см$. Все частицы одновременно освобождают.

Каковы будут их скорости, когда они разлетятся на значительные расстояния друг от друга?

A H

Частицы можно рассматривать как классические точечные массы, перемещающиеся в электрических полях друг друга. Гравитационным взаимодействием частиц можно пренебречь.

194 В эксперименте по комптоновскому рассеиванию неподвижные электроны бомбардируются фотонами, энергия которых равна энергии покоя электрона.

a Найдите угол между рассеянными фотонами и электронами, импульсы которых имеют одинаковую величину.

A H

b Какова скорость таких электронов?

A