
We will use a coordinate system with axes parallel to the cube’s edges, with the origin set at the cube’s center. Assuming the particle is at coordinates $(x, y, z)$ $x\ll a$, $y\ll a$, $z\ll a$, we will find the force $\vec{F}$ acting on the particle, by splitting the cube $a\times a\times a$ into a rectangular cuboid $(a - 2x)\times (a - 2y)\times (a - 2z)$ and three square plates of thickness $2x$, $2y$ and $2z$.
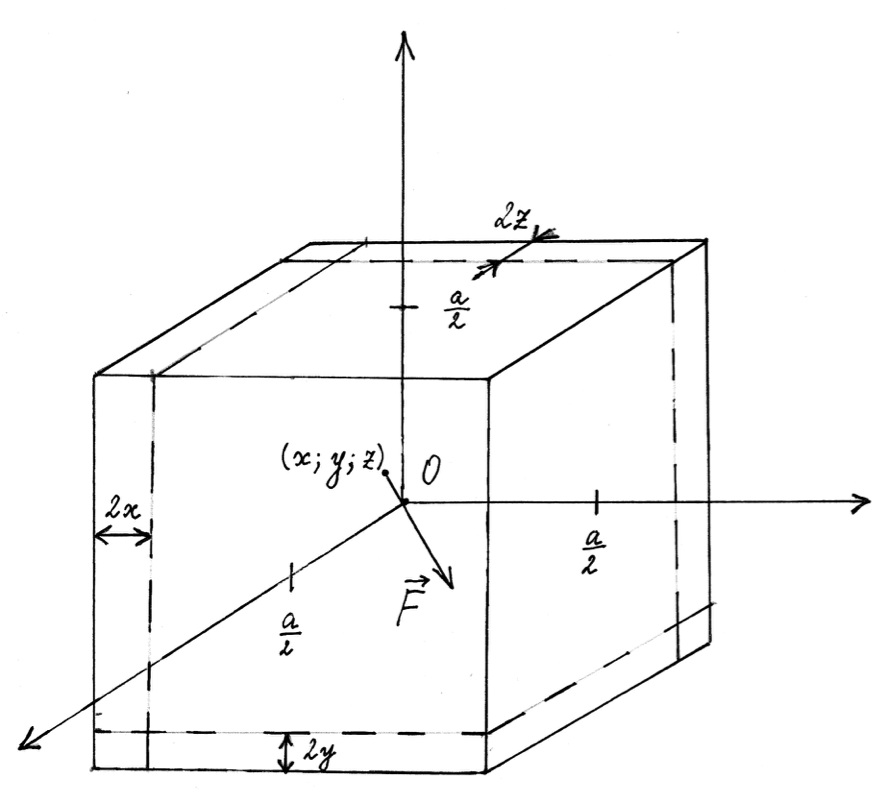
The particle is in the center of the cuboid, so there is no force from the cuboid.
Let us find the force between a particle with a charge $q$ and a uniformly charged square plate of small thickness $h$ and edge length $a$. The plate’s charge density is $\rho$, the particle is placed above the center of the plate at distance $a/2$.
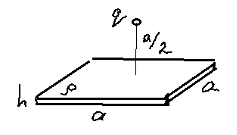
Due to symmetry and Gauss’s law, the flux of the particle’s electric field through the plate is
$$
\Phi = \frac{q}{6\varepsilon_0}.
$$
Hence, the force
$$
F = \sigma\Phi = \frac{q\rho h}{6\varepsilon_0},
$$
where $\sigma = \rho h$ is plate’s surface charge density.
Three square plates act on the particle with forces $\vec{F_1} = \frac{q\rho x}{3\varepsilon_0}\hat{x}$, $\vec{F_2} = \frac{q\rho y}{3\varepsilon_0}\hat{y}$, and $\vec{F_3} = \frac{q\rho z}{3\varepsilon_0}\hat{z}$. Net force $\vec{F} = \vec{F_1} + \vec{F_2} + \vec{F_3} =
\frac{q\rho}{3\varepsilon_0}\vec{r},$ where $\vec{r}$ is the position vector of the particle.
The particle’s equation of motion
$$
m\vec{\ddot{r}} = \frac{q\rho}{3\varepsilon_0}\vec{r}
$$
is an equation of simple harmonic motion with period
$$
T = 2\pi\sqrt{\frac{3m\varepsilon_0}{q(-\rho)}}.
$$