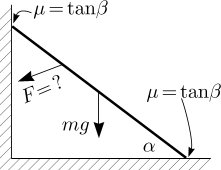
Однородный тонкий стержень массы $m$ поставили в угол, образованный вертикальной стеной и горизонтальным полом. Угол между стержнем и полом $\alpha$. Ось стержня и ребро двугранного угла перпендикулярны. Коэффициент трения между стержнем и поверхностями равен $\mu=\mathrm{tg}\,\beta$, и он недостаточно велик, чтобы удержать стержень в таком положении (считая, что к стержню приложены только силы реакции опоры и сила тяжести).