
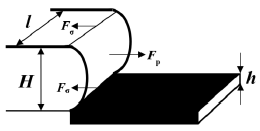
В результате на нижнюю поверхность пластинки площадью \( S=a^{2} \) действует разность давлений \( \Delta p=\rho_{0} g(H+h) \), что приводит к появлению направленной вертикально вверх силы \( F=\Delta p S \). Для определения величины \( H \) выделим некоторый объем воды шириной \( l \) вблизи ее контакта с пластинкой. На него действует сила поверхностного натяжения, равная \( F_{\sigma}=2 \sigma l \) а также сила, обусловленная давлением столба жидкости \( F_{\bar{p}}=\bar{p} \Delta S \), где среднее давление записывается как
\[
\bar{p}=\frac{1}{2} \rho_{0} g H
\]
при площади сечения \( \Delta S=H l \)
Из условия равновесия воды
\[
F_{\sigma}=F_{\bar{p}}
\]
следует, что перепад высот равен \( H=2 \sqrt{\cfrac{\sigma}{\rho_{0} g}} \)
На дополнительный груз на пластинке действует сила тяжести, равная \( F_{m}=m g \)
и из условия равновесия \( F_{p}+F_{m}=F \) находим массу груза