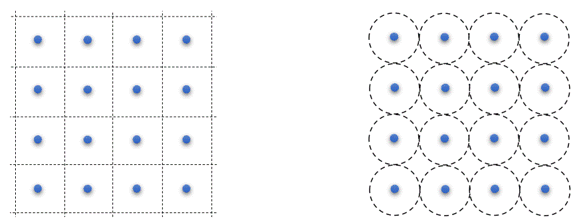
Плазма считается четвертым состоянием вещества и представляет собой ионизованный газ, содержащий электроны, ионы и нейтральные частицы. В плазме концентрации частиц и температура изменяются в очень широких пределах, так что в ней существенную роль могут играть самые раз-нообразные физические эффекты. Поэтому в настоящее время разработано большое количество мо-делей плазмы и в этой задаче речь пойдет об одной из них, которая называется моделью однокомпонентной среды. Именно, рассмотрим полностью ионизованную плазму, в которой отсутствуют нейтральные частицы, и которая состоит из положительно заряженных ядер дейтерия, движущихся на однородно заряженном по объему нейтрализующем фоне, образуемом электронами. Такая модель является очень хорошим приближением для плазмы сверхвысоких давлений, реализующихся в цен-тре белых карликов и планет-гигантов типа Юпитера. Пусть заряд ядер дейтерия и их масса равны $e=1.602\cdot 10^{-19} \text{Кл}$ и $m=3.44\cdot 10^{-24} \text{г}$, а их концентрация составляет $n=1.62\cdot 10^{27} \text{см}^{-3}$ при температуре $T=1.76\cdot 10^4 \text{К}$. При данных условиях существенную роль играет взаимодействие между ядрами дейтерия, которые располагаются в узлах кубической решетки, двумерная проекция которой показана на рисунке 1 (слева). Плазма в целом является нейтральной, поэтому каждый кубик с расположенным в центре ядром является незаряженным и называется элементарной ячейкой. Поле, создаваемое каждой кубической ячейкой, является очень сложным, и вместо этого рассматривают сферические ячейки, двумерная проекция которых показана на рисунке 1 (справа). Возможность такой замены не является очевидной и зависит от типа рассматриваемых задач.

В численных расчетах считайте известными значения следующих постоянных: постоянная Больцмана $k=1.38\cdot 10^{-23}$ \text{Дж/К}, диэлектрическая постоянная $\varepsilon_0=8.85\cdot 10^{-12} \text{Ф/м}$.

1  ^0.40 Рассчитайте наименьшее расстояние $a$ между соседними ядрами.

2  ^0.80 Покажите, что энергия ядер играет существенную роль в данных условиях. Для этого оцените отношение $\Gamma$ энергии взаимодействия соседних ядер к их тепловой энергии. Наличием нейтрализующего фона пренебречь.

3  ^0.60 Рассчитайте объемную плотность заряда $\rho$ сферической ячейки в однокомпонентной модели плазмы.

4  ^1.40 Рассчитайте разность потенциалов между двумя точками сферической ячейки, расположенными на расстоянии $a/2$ и $a/4$.

5  ^0.60 Рассчитайте частоту малых колебаний ядер $\omega_p$ возле положения равновесия в сферической ячейке.

6  ^0.60 При заданной температуре плазмы оцените среднеквадратичную амплитуду $A$ колебаний ядер вблизи положения их равновесия.

7  ^1.80 Внутренняя энергия $U$ однокомпонентной плазмы объемом $V$, содержащей $N$ сферических ячеек, имеет вид
$$
U=\alpha_1 N+\alpha_2\cfrac{N^{4/3}}{V^{1/3}}.
$$
Найдите постоянные $\alpha_1$ и $\alpha_2$.

Плазменное состояние вещества является перспективным рабочим телом для осуществления управляемой реакции ядерного синтеза. Основная проблема в осуществлении ядерного синтеза заключается в преодолении кулоновского отталкивания между положительно заряженными ядрами, называемого кулоновским барьером. Наличие у ядер нейтрализующего фона приводит к снижению кулоновского барьера, так как уменьшается сила отталкивания между ядрами. Рассмотрим процесс слияния двух ячеек, который происходит следующим образом. Две ячейки сливаются в одну сферическую ячейку с той же самой величиной объемной плотности нейтрализующего фона, а в центре появляется новое ядро, образованное слиянием двух исходных ядер.

8  ^1.20 Рассчитайте снижение кулоновского барьера $\delta U_c$ для слияния двух ячеек ядер дейтерия при заданных условиях.

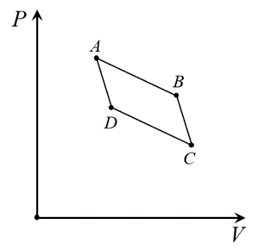
9  ^1.00 Используя приведенный выше цикл, выразите производную внутренней энергии по объему при фиксированной температуре $\left(\cfrac{\partial U}{\partial V}\right)_T$ через производную давления по температуре при фиксированном объеме $\left(\cfrac{\partial P}{\partial T}\right)_V$, а также температуру $T$ и давление $P$ системы.

10  ^1.60 Давление $P$ однокомпонентной плазмы объемом $V$, содержащей $N$ сферических ячеек, имеет вид
$$
P=\beta_1\cfrac{N}{V}+\beta_2\left(\cfrac{N}{V}\right)^{\beta_3}.
$$
Найдите постоянные $\beta_1, \beta_2$ и $\beta_3$. Рассчитайте численное значение давления при заданных в условии задачи значениях параметров плазмы.