Волоконная брэгговская решётка — это оптическое устройство, в котором периодически меняется показатель преломления среды.

Пусть показатель преломления материала сердцевины волоконной решётки равен $n_1 = 1.51$, а показатель преломления изменённых частей $n_2 = 1.55$. Слои с показателями преломления $n_2$ и $n_1$ имеют толщины $d_2$ и $d_1$ соответственно и располагаются поочерёдно, общее число слоёв равно $N$. Продольный разрез решётки показан на рисунке (a). В процессе проектирования устройств обычно учитывают только однократное отражение от каждой границы раздела слоев и игнорируют поглощение в среде.

1  ^20.00 Пусть длина волны используемого света в вакууме составляет $\lambda = 1.06~\text{мкм}$. Какими должны быть минимальные толщины слоёв $d_1$ и $d_2$, чтобы отражённый свет конструктивно интерферировал? Каким должно быть при этом наименьшее число $N$ слоёв, чтобы коэффициент отражения достигал $8\%$?

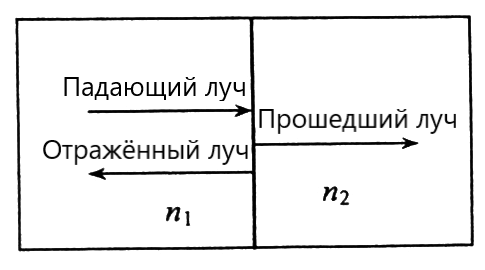
$\textit{Подсказка}$: Как показано на рисунке (b), когда свет падает перпендикулярно из среды с показателем преломления $n_1$ в среду с $n_2$, для отражённого и прошедшего лучей справедливы формулы:$$\frac{\text{амплитуда отраженного луча}}{\text{амплитуда падающего луча}}=\frac{n_1 - n_2}{n_1 + n_2}$$$$\frac{\text{амплитуда прошедшего луча}}{\text{амплитуда падающего луча}} = \frac{2n_1}{n_1+n_2}$$$$\text{коэффициент отражения} =
\bigg( \frac{\text{амплитуда отраженного луча}}{\text{амплитуда падающего луча}} \bigg)^2$$