1
14.00
Если две боеголовки могут поразить цели $W$ и $N$ соответственно, определите положение подводной лодки во время запуска бомбы, определите направление запуска и укажите условия, при которых такой запуск возможен.
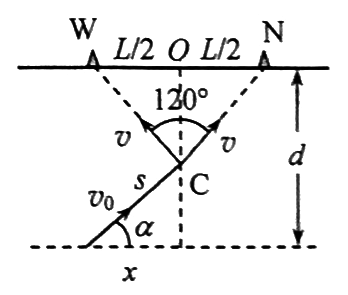
Ответ:
Если бомба разделяется над водой, то
$x = \pm \sqrt{\frac{4 L^2}{9 v^4}(3 v_0^2 v^2 - g^2 L^2) - (d - \frac{L}{2 \sqrt3})^2}$,
$\cos{\alpha} = \sqrt{1 - \frac{9 v^4 \big( d - \frac{L}{2 \sqrt3} \big)^2}{L^2 (3 v_0^2 v^2 - g^2 L^2)}}$, $\sin{\alpha} = \pm \frac{(2\sqrt3d - L)v}{4Lv_0 \sqrt{1 - \frac{g^2 L^2}{3 v_0^2 v^2}}}$.
Условия возможности пуска:
$0 < \frac{gL}{\sqrt3v_0v} \leq 1$, $\Bigg| \frac{(2\sqrt3d - L)v}{4Lv_0 \sqrt{1 - \frac{g^2 L^2}{3 v_0^2 v^2}}} \Bigg| \leq 1$, $d > 0$.
Если бомба разделяется над землёй, то
$x = \pm \sqrt{\frac{4 L^2}{9 v^4}(3 v_0^2 v^2 - g^2 L^2) - (d + \frac{L}{2 \sqrt3})^2}$,
$\sin{\alpha} = \frac{(2\sqrt3d + L)v}{4Lv_0 \sqrt{1 - \frac{g^2 L^2}{3 v_0^2 v^2}}} \leq 1$.

