1  ^?? Предполагая, что угол между результирующим импульсом ядра-мишени и начальным импульсом налетающего нейтрона равен $\alpha$, выразите результирующие скорости ядра $v_1$ и нейтрона $v$ через начальную скорость нейтрона $v_0$.

2  ^?? По этим данным найдите значения $m$ и $v_0$.

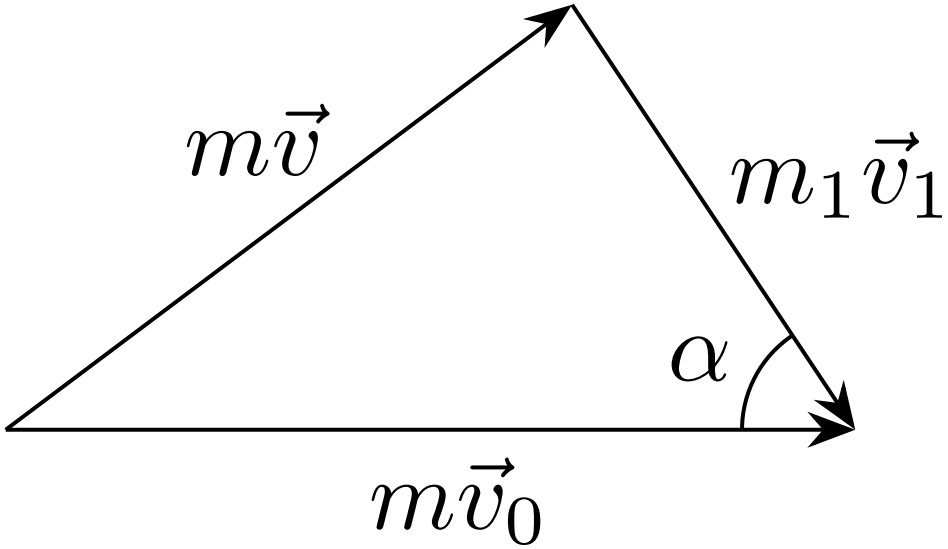
Максимальная величина скорости $v_1$ достигается при угле $\alpha=0$, при котором:\[v_{1\max}=\frac{2m}{m+m_1}v_0.\]Тогда максимальные скорости ядер водорода и азота будут равны соответственно\[\begin{cases}v_{\mathrm H}=\frac{2m}{m+m_{\mathrm H}}v_0,\\ v_{\mathrm N}=\frac{2m}{m+m_{\mathrm N}}v_0=\frac{2m}{m+14m_{\mathrm H}}v_0\end{cases}\]Решая полученную систему относительно $m$ и $v_0$, получим:

Наконец, скорость\[v_0=\frac{m+m_{\mathrm H}}{2m}v_{\mathrm H}=\frac{13v_{\mathrm H}v_{\mathrm N}}{2(14 v_{\mathrm N}-v_{\mathrm H})}.\]

3  ^?? Найдите, после какого числа $n$ таких столкновений кинетическая энергия ядра азота приблизительно сравняется с кинетической энергией налетающих нейтронов.

Пусть после $i$-того столкновения скорость ядра азота равна $V_i$. Добавка с скорости ядра при столкновении будет максимальна, если происходит лобовое столкновение. Таким образом, законы сохранения энергии и импульса для $i+1$-того столкновения имеют вид:\[\begin{cases}mv_0+m_{\mathrm N}V_i=mv_0'+m_{\mathrm N}V_{i+1}\\\frac{1}{2}mv_0^2+\frac{1}{2}m_{\mathrm N}V_i^2=\frac{1}{2}mv_0^{\prime2}+\frac{1}{2}m_{\mathrm N}V_{i+1}^2\end{cases}.\]Исключая из этой системы $v'_0$, получим рекуррентное уравнение на $V_i$:\[\frac{V_{i+1}}{v_0}=1-a+a\frac{V_{i}}{v_0},\]где $a\equiv\frac{m_{\mathrm N}-m}{m_{\mathrm N}+m}=0.847$. Из этого уравнения несложно получить общее выражение для $V_n$:\[\frac{V_n}{v_0}=1-a+a\frac{V_{n-1}}{v_0}=1-a+a\left(1-a+a\frac{V_{n-2}}{v_0}\right)=1-a^2+a^2\frac{V_{n-2}}{v_0}=\ldots=1-a^3+a^3\frac{V_{n-3}}{v_0}=\ldots=1-a^n+a^n\frac{V_0}{v_0}.\]Так как по условию $V_0=0$, то\[V_n=\left(1-a^n\right)v_0.\]Кинетическая энергия ядра азота приблизительно сравняется с кинетической энергией налетающих нейтронов, когда\[\frac{1}{2}m_{\mathrm N}V_n^2=\frac{1}{2}\cdot1.16m_{\mathrm H}v_0^2\implies (1-a^n)^2=\frac{1.16}{14}\implies n=\frac{\ln\left(1-\sqrt{1.16/14}\right)}{\ln a}=2.04\approx2.\]

4  ^?? Найдите кинетическую энергию $E_p$, соответствующую наиболее вероятной скорости нейтронов, и наиболее вероятную кинетическую энергию $E_{kp}$.

Наиболее вероятную скорость нейтронов $v_p$ можно определить из уравнения:\[0=\frac{\mathrm df(v)}{\mathrm dv}=4\pi \left( \frac{m}{2 \pi k_B T} \right)^{3/2} e^{-\frac{mv^2}{2k_BT}}\left[2v+v^2\cdot\left(-\frac{m\cdot 2v}{2k_BT}\right)\right]\implies v_p=\sqrt{\frac{2k_BT}{m}}.\]Этой скорости соответствует кинетическая энергия\[E_p=\frac{1}{2}mv_p^2=k_BT.\]

Чтобы перейти к распределению по энергиям (вместо распределения по скоростям), запишем:\[\mathrm dN=f(v)~\mathrm dv=f(E_k)~\mathrm dE_k,\]где $N$ — число частиц. Поскольку $\mathrm dE_k=mv~\mathrm dv$, то $\mathrm dv=\frac{\mathrm dE_k}{\sqrt{2mE_k}}$, тогда распределение по энергиям:\[f(E_k)=\frac{1}{\sqrt{2mE_k}}\cdot 4\pi \left( \frac{m}{2 \pi k_B T} \right)^{3/2} \cdot \frac{2E_k}{m}\cdot e^{-\frac{E_k}{k_BT}}=\frac{2\pi}{(\pi k_BT)^{3/2}}\cdot E_k^{1/2}e^{-\frac{E_k}{k_BT}}.\]Наиболее вероятная кинетическая энергия находится из уравнения:\[0=\frac{\mathrm df(E_k)}{\mathrm dE_k}=\frac{2\pi}{(\pi k_BT)^{3/2}}\cdot e^{-\frac{E_k}{k_BT}}\left[\frac{1}{2\sqrt{E_k}}+\sqrt{E_k}\cdot\left(-\frac{1}{k_BT}\right)\right]\implies\]