2
10.00
На рисунке показана $P-V$ диаграмма так называемого цикла Отто, где $A \to B$ $C \to D$ — изохорические, а $B \to C$ и $D \to A$ — адиабатические процессы. Изобразите на схематичной диаграмме, как при этом меняются величины $E_1$ и $p_1$, найдите подведённую/отведённую теплоту, изменение внутренней энергии и совершённую работу для каждого из процессов цикла.
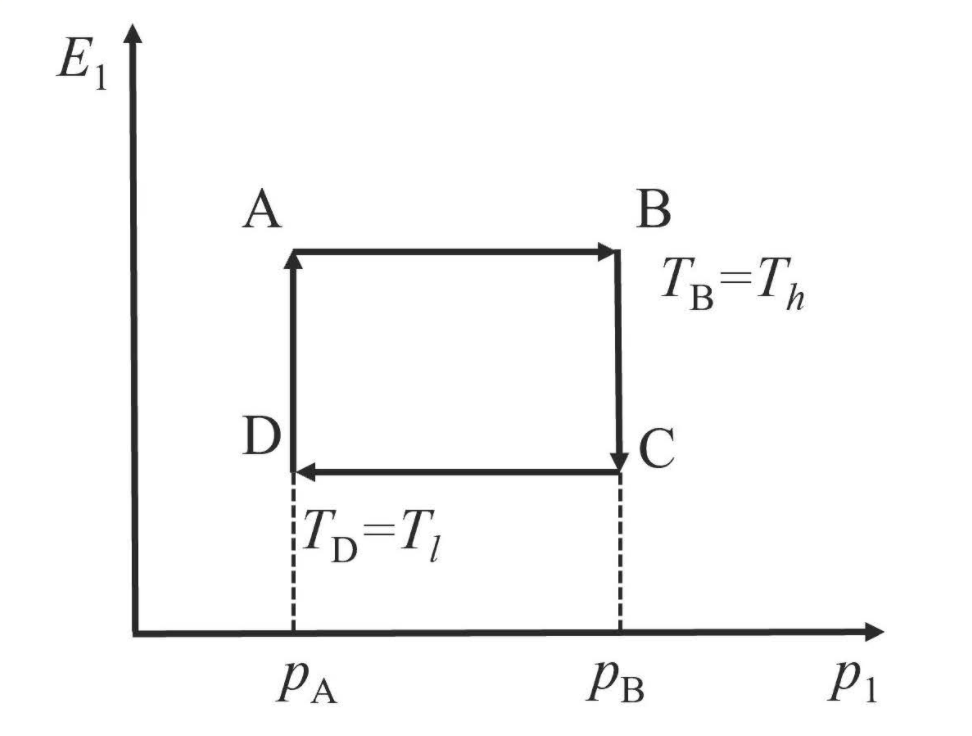
Ответ:
В $A \to B$: $Q_1 = \Delta_1 \langle E \rangle = E_B (p_B - p_A),\,W_1 = 0;$
в $B \to C$: $W_2 = -\Delta_2 \langle E \rangle = (E_B - E_C) p_B,\,Q_2 = 0;$
в $C \to D$: $Q_3 = -\Delta_3 \langle E \rangle = E_D (p_B - p_A),\,W_3 = 0;$
в $D \to A$: $W_4 = -\Delta_4 \langle E \rangle = (E_D - E_A) p_A,\,Q_4 = 0.$

