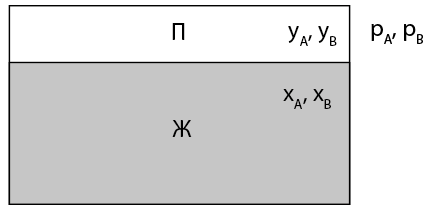
Давление насыщенных паров над поверхностью смеси двух идеально смешиваемых жидкостей ($A$) и ($B$) подчиняется закону Рауля:
$$
P_A=p_A x_A\\
P_B=p_B x_B,
$$
где $p_A$, $p_B$ — давления насыщенных паров чистых жидкостей $A$ и $B$, $x_A$ и $x_B$ — молярные доли компонент жидкости в смеси ($x_A+x_B=1$).

A1 Дано $p_A$, $p_B$, $x_A$ , $x_B$. Найти молярные доли компонент смеси в газообразной фракции ($y_A$ и $y_B$).

S

Давление насыщенного пара над поверхностью чистой жидкости зависит от температуры. Эту зависимость можно восстановить, рассматривая цикл Карно, где в качестве рабочего тела используется двухфазная система «жидкость-пар».

A2 Пусть для жидкости известны молярная теплота парообразования $\lambda$ и температура кипения жидкости $t$ при атмосферном давлении $P_0$. Найдите зависимость давления насыщенного пара чистой жидкости от температуры $P(T)$.

S

A3 Выразите $p_A/p_B$ при температуре $T$ через температуры кипения чистых жидкостей $t_A$ и $t_B$ (при атмосферном давлении), их молярные теплоты парообразования $\lambda_A$ и $\lambda_B$.

S

A4 Считая $\lambda_A=\lambda_B=\lambda$, найдите температуру кипения двухкомпонентной смеси: $T(\lambda,t_A,t_B,x_B)$.

S

A5 Считая температуру двухкомпонентной системы $T$ постоянной, изобразите на графиках зависимости $P(x_B) , P(y_B)$ и $y_B(x_B)$.

S

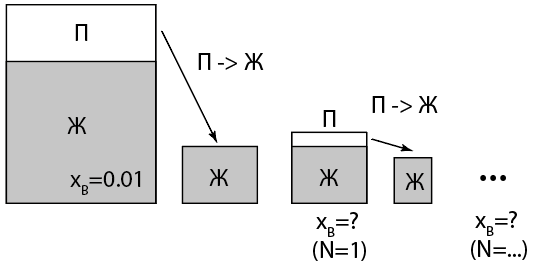
В двухкомпонентной системе двух жидкостей с $p_B=2 p_A$, в начальный момент $x_B=0.01$. Пар над жидкостью собирают и изотермически конденсируют.

A6 Какая $x_B$ будет достигнута после первой конденсации ($N=1$)?

S

После первой конденсации объем сосуда изотермически немного увеличивают, чтобы в небольшом объеме снова возник насыщенный пар, этот пар собирают и процедура повторяется $N$ раз.

A7 Какая $x_B$ будет достигнута после того как процедура повторится $N=10$ раз, $N= 10^6$?

S

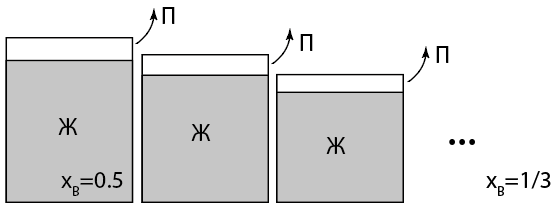
В двухкомпонентной системе двух жидкостей с $p_B=2 p_A$, в начальный момент $x_B=0.5$. В начальный момент объем сосуда лишь немного превышает объем жидкости, далее пар над поверхностью жидкости медленно откачивают, а объем сосуда уменьшают так, чтобы объем пара всегда был много меньше объема жидкости. В течение всего процесса температура $T$ остается постоянной. Молярные плотности смешиваемых жидкостей считать равными. Спустя продолжительное время молярная доля жидкости $B$ в смеси достигла $x_B=1/3$.

A8 Найдите, во сколько раз к этому моменту уменьшилось общее количество жидкости?

S