
По мере развития промышленности возникала необходимость работы с газами. Нужна была их добыча, транспортировка, хранение, и любой из этих этапов требовал расчетов состояния газов. Сформулированная модель идеального газа уже в середине XIX века перестала удовлетворять промышленников, работавших с газами под большими давлениями и низкими температурами. Соответственно, были сделаны попытки предложить уточненные модели, описывающие состояния газов. Взаимодействия между молекулами газа довольно сложны, поэтому простая модель вряд ли возможна. Но промышленникам в значительной степени не требовалась идеально выверенная физическая модель, их вполне устраивали эмпирические уравнения состояния, которые предлагались учеными. В этой задаче вы, используя метод наименьших квадратов, попробуете определить параметры зависимостей в ряде моделей. Затем, построив исходные данные и смоделированную зависимость на одном графике, визуально оцените удовлетворительность модели.
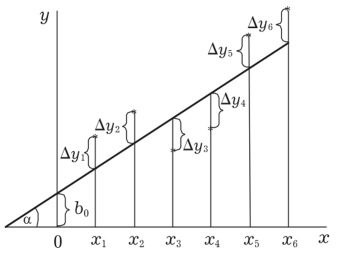
Рассмотрим, как это работает, на примере хорошо вам известной линейной зависимости. Фитирующая функция — это $f(x)=kx+b$. Минимизируем следующую сумму: $S= \sum_n~(y_i-kx_i-b)^2$. Согласно тому, что написано выше, получим систему
\begin{equation}
\begin{cases}
\cfrac{\partial S}{\partial k}=0=\sum_n~2(y_i-kx_i-b)(-x_i)\\
\cfrac{\partial S}{\partial b}=0=\sum_n~2(y_i-kx_i-b)(-1)
\end{cases}
\end{equation}
Оба уравнения можно разделить на 2 и ничего не изменится. Таким образом, получим:
\begin{equation}
\begin{cases}
\sum_n~(-x_iy_i)+\sum_n~kx_i^2+\sum_n~bx_i=0\\
\sum_n~(-y_i)+\sum_n~kx_i+\sum_n~b=0
\end{cases}
\end{equation}
и далее, вынося из-под знака суммы величины $k$ и $b$,
\begin{equation}
\begin{cases}
\sum_n~x_iy_i=k\sum_n~x_i^2+b\sum_n~x_i\\
\sum_n~y_i=k\sum_n~x_i+b\sum_n~1
\end{cases}
\end{equation}
видно, что мы получили систему линейных уравнений на параметры $k$ и $b$, решив ее, мы найдем те параметры $k$ и $b$, которые минимизируют исходную сумму. Коэффициенты в системе уравнений — это просто суммы по всему набору данных следующих величин $(x_iy_i), (x_i)^2, x_i, y_i$. Последний коэффициент $\sum_n~1$ перед $b$ — это просто число точек с данными, т.е. $\sum_n~1=n$.
Решив систему уравнений относительно $k$ и $b$, получим:
$$
k=\cfrac{-n\sum_n~x_iy_i+\sum_n~x_i\sum_n~y_i}{-n\sum_n~x_i^2+\left(\sum_n~x_i\right)^2}
$$
$$
b=\cfrac{-\sum_n~x_i\sum_n~x_iy_i+\sum_n~x_i^2\sum_n~y_i}{-\left(\sum_n~x_i\right)^2+n\sum_n~x_i^2}
$$
Если числитель и знаменатель каждого выражения поделить на $n^2$, то получатся более изящные формулы:
$$
k=\cfrac{-\overline{xy}+\overline x\,\overline y}{-\overline{x^2}+\overline x^2}
$$
$$
b=\cfrac{-\overline x\,\overline{xy}+\overline{x^2}\,\overline y}{-\overline x^2+\overline{x^2}}
$$
где черта означает усреднение величины по всему набору данных.
По этим формулам и вычисляют параметры моделирующей зависимости ваши калькуляторы и компьютеры. В некоторых случаях, когда вы можете линеаризовать зависимость, то, что описано выше, конечно тоже применимо. В случаях, когда зависимость линеаризовать не получается, приходится с нуля оптимизировать коэффициенты (и, вообще говоря, это не всегда удается, это зависит от функции).
Внимание! В разбалловке будут поставлены очень узкие ворота на диапазон определяемых величин. Выражения, по которым вы будете рассчитывать оптимальные значения величин, должны быть записаны в виде сумм или средний значений величин. Предполагается, что все расчеты вы будете делать численно, считая суммы, подобные описанным выше. Вероятно, графические методы решения в некоторых пунктах, не дадут необходимую точность. Погрешности оценивать не нужно.
Для одного моля некоторого неидеального газа была снята зависимость $T(V)$ на изобаре $p=2~МПа$. Таблица данных приведена в листе ответов. Зависимость имеет слегка нелинейный характер, и вашей задачей будет поиск подходящей модели, чтобы ее описать.
Смоделируем состояние газа уравнением $(p+a_0)V=RT$. Нужно подобрать такое значение $a_0$, которое минимизировало бы сумму квадратов отклонений экспериментальных точек от модельной кривой.
Смоделируем состояние газа уравнением $(p+\cfrac{a_1}{V})V=RT$. Нужно подобрать такое значение $a_1$, которое минимизировало бы сумму квадратов отклонений экспериментальных точек от модельной кривой.
Смоделируем состояние газа уравнением $(p+\cfrac{a_2}{V^2})V=RT$. Нужно подобрать такое значение $a_2$, которое минимизировало бы сумму квадратов отклонений экспериментальных точек от модельной кривой.
Смоделируем состояние газа уравнением $(p+\cfrac{c}{V^2}+\cfrac{d}{V^3})V=RT$. Нужно подобрать такие значения $c$ и $d$, которые минимизировали бы сумму квадратов отклонений экспериментальных точек от модельной кривой.
Смоделируем состояние газа уравнением $(p+\cfrac{a}{V^2})(V-b)=RT$. Нужно подобрать такие значения $a$ и $b$, которые минимизировали бы сумму квадратов отклонений экспериментальных точек от модельной кривой.