1  ^24.00 Считая деформацию пружины упругой, найдите скорость каждого из шариков произвольный момент времени $t$ $(t>0)$.

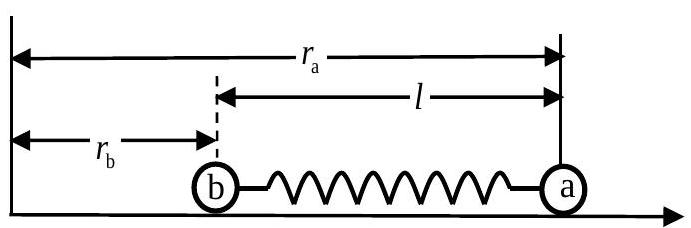
Пусть удлинение пружины в момент $t$ составляет$$
u=l-l_{0}.
$$Тогда уравнение движения:\begin{equation*}
\mu \frac{d^{2} u}{d t^{2}}=-k_{0} u ,\tag{1}
\end{equation*}где $\mu$ — приведённая масса двух шариков:\begin{equation*}
\mu=\frac{m_am_b}{m_a+ m_b}.\tag{2}
\end{equation*}Отсюда следуем, что удлинение пружины $u$ подчиняется уравнению гармонических колебаний с частотой\begin{equation*}
f=\frac{\omega}{2 \pi}=\frac{1}{2 \pi} \sqrt{\frac{k_{0}}{\mu}}=\frac{1}{2 \pi} \sqrt{\frac{m_a+m_b}{m_am_b} k_{0}}. \tag{3}
\end{equation*}Зависимость удлинения пружины от времени может быть представлена в виде:\begin{equation*}
u(t)=A \sin \omega t+B \cos \omega t, \tag{4}
\end{equation*}где $A$ и $B$ — константы, определяемые из начальных условий. При $t=0$ пружина не деформирована, поэтому$$
u(0)=B=0,
$$поэтому:\[u=A \sin \omega t \tag{5}\]Скорость шарика $a$ относительно шарика $b$ равна\begin{equation*}
v'_a=\frac{\mathrm d r_a}{\mathrm d t}-\frac{\mathrm d r_b}{\mathrm d t}=\frac{\mathrm d u}{\mathrm d t}=A \omega \cos \omega t .\tag{6}
\end{equation*}В начальный момент времени:\begin{equation*}
v_{\mathrm{a}}^{\prime}(0)=v_{0}-0=A \omega. \tag{7}
\end{equation*}Из уравнений $(6)$ и $(7)$ имеем\begin{equation*}
v_{\mathrm{a}}^{\prime}=v_{0} \cos \omega t .\tag{8}
\end{equation*}Поскольку при движении системы имеет место закон сохранения импульса, то:\begin{equation*}
m_av_{0}=m_av_a+m_bv_b. \tag{9}
\end{equation*}Скорость шарика $a$ относительно земли равна\begin{equation*}
v_a=v'_a+v_b. \tag{10}
\end{equation*}Из уравнений $(3)$, $(8)$, $(9)$ и $(10)$ скорости шариков в момент времени $t$ равны:

2  ^11.00 Найдите величину заряда $q$ шариков и частоту $f$ малых колебаний системы.

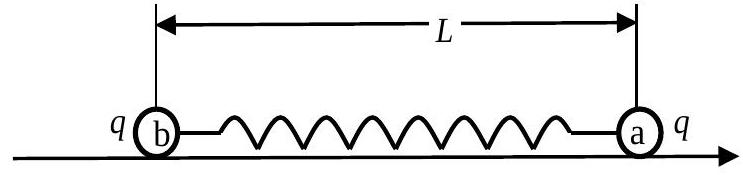
Условие равновесия системы:
\begin{equation*}
K \frac{q^{2}}{L_{0}^{2}}=k_{0}\left(L_{0}-l_{0}\right), \tag{13}
\end{equation*}откуда:

Пусть длина пружины в момент времени $t$ равна $L$ (см. рис. 2), тогда:\begin{equation*}
\mu \frac{\mathrm d^{2} L}{\mathrm d t^{2}}=-k_{0}\left(L-l_{0}\right)+K \frac{q^{2}}{L^{2}}. \tag{15}
\end{equation*}Обозначим $x$ удлинение пружины $L-L_{0}$ в момент времени $t$. Уравнение $(15)$ может быть переписано как:\begin{equation*}
\mu \frac{\mathrm d^{2} x}{\mathrm d t^{2}}=-k_{0} x-k_{0}\left(L_{0}-l_{0}\right)+K \frac{q^{2}}{L_{0}^{2}}\left(1+\frac{x}{L_{0}}\right)^{-2} .\tag{16}
\end{equation*}Так как при малых колебаниях $x\ll L_{0}$, то\begin{equation*}
\left(1+\frac{x}{L_{0}}\right)^{-2}\approx 1-2 \frac{x}{L_{0}},\tag{17}
\end{equation*}и уравнение $(16)$ упрощается до:\begin{equation*}
\mu \frac{\mathrm d^{2} x}{\mathrm d t^{2}}=\left[-k_{0}\left(L_{0}-l_{0}\right)+K \frac{q^{2}}{L_{0}^{2}}\right]-\left(k_{0}+2 K \frac{q^{2}}{L_{0}^{3} }\right) x. \tag{18}
\end{equation*}Используя уравнение $(13)$ или $(14)$, уравнение $(18)$ можно переписать как:\begin{equation*}
\mu \frac{d^{2} x}{d t^{2}}=-\left(k_{0}+2 K \frac{q^{2}}{L_{0}^{3}}\right) x=-\frac{3 L_{0}-2 l_{0}}{L_{0}}{L_{0}} k_{0} x \tag{19}
\end{equation*}Из уравнения $(13)$ следует, что $L_{0}>l_{0}$, поэтому $3 L_{0}-2 l_{0}>0$. Значит, движение системы действительно представляет собой гармонические колебания, частота которых составляет: