В июне 2021 года пилотируемый корабль «Шэньчжоу-12» был успешно состыкован с космической станцией «Тяньгун», для чего необходимо было решить проблему встречи объекта-преследователя («Шэньчжоу-12») и цели (космической станции) на околоземной орбите. В этой задаче рассматривается использование гомановской траектории для изучения того, как объект должен менять свои скорость и направление движения, чтобы встретиться с целью на орбите.

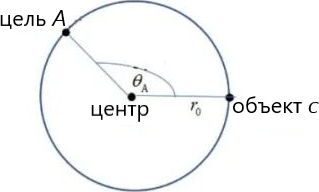
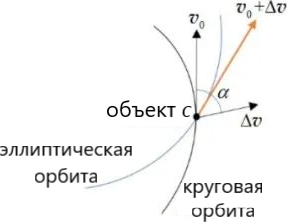
Как показано на рисунке (a), изначально цель $A$ и объект $c$ движутся по круговой орбите радиусом $r_0$ против часовой стрелки со скоростью $v_0$. Их положения в момент времени $t=0$:\[\theta_{A,i}=\theta_0,\ \theta_{c,i}=0,\ r_{A,i}=r_{c,i}=r_0.\]В этот момент включается двигатель объекта $c$, и его скорость мгновенно получает приращение $\Delta\vec v$, как показано на рисунке (b). Благодаря этому орбита $c$ также мгновенно меняется с круговой радиусом $r_0$ на эллиптическую орбиту, показанную на рисунке (c). Угол между большой полуосью новой орбиты и полярной осью (проходящей через центр и начальное положение $c$) обозначим $\phi$ ($\phi$ отсчитывается по часовой стрелке), угол между радиус-вектором $c$ и полярной осью обозначим $\theta_c$ (отсчитывается против часовой стрелки), а расстояние между центром и $c$ — $r_c(\theta_c)$.

Известно, что эллиптическая орбита, большая полуось которой лежит на полярной оси, а начало координат которой представляет собой её правый фокус, задаётся в полярных координатах в виде:\[r(\theta)=\frac R{1+\varepsilon\cos\theta},\]где $R$ — фокальный параметр орбиты, а $\varepsilon$ — её эксцентриситет.

1 Если масса объекта $m$, его полная механическая энергия $E$ и момент импульса $L$ известны, выразите через эти величины и $r_0$, $v_0$ параметры орбиты $R$ и $\varepsilon$.

A

2 Запишите уравнение орбиты $r_c(\theta_c)$ объекта после ускорения через $r_0$, эксцентриситет $\varepsilon$ и $\phi$.

A

3 Найдите отношение $\frac{T_c}{T_A}$ периодов обращения объекта и цели. Ответ выразите через $\varepsilon$ и $\phi$.

A

4 Определим два безразмерных параметра ускорения (см. рисунок (b)): безразмерное изменение скорости $\delta=\frac{|\Delta\vec v|}{|\vec v_0|}$ и угол $\alpha$ между $\vec v$ и $\Delta\vec v$ (отсчитывается по часовой стрелке). Выразите через $\delta$ и $\alpha$ величины $\varepsilon$ и $\varepsilon\cos\phi$ для орбиты объекта $c$.

A

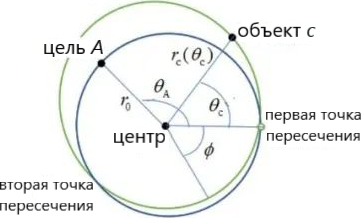
Рассмотрим ситуацию, когда объект $c$ и цель $A$ встречаются в первой точке пересечения их орбит (см. рисунок (c)). Пусть цель $A$ проходит через эту точку $n_A$ раз с момента времени $t=0$, а объект $c$, не учитывая его начальное положение, — $n_c$ раз. В момент времени $t=0$:\[\theta_{A,i}=\theta_0,\ \theta_{c,i}=0.\]

5 Выразите $n_A$ через $n_c$, $\theta_0$, $\varepsilon$ и $\phi$.

A

6 Выразите $n_A$ через $\delta$ и $\alpha$ и найдите при фиксированной $\delta$ два очевидных экстремума $\alpha_0$ функции $n_A(\alpha)$ (экстремальность гарантирует, что даже если $\alpha$ немного отклонится $\alpha_0$ из-за неидеального позиционирования объекта, решение всё равно будет примерно верное, что очень удобно при стыковке).

A

Выберите одно из найденных вами значений $\alpha_0$.

7.1 $\delta$ имеет верхний предел $\delta_\max$ (т.е. при $\delta > \delta_\max$ объект $c$ не встретится с целью $A$). Найдите $\delta_\max$.

A

7.2 Пусть $\theta_{A,i}=\theta_0$. Найдите соотношение между $\delta$, $\theta_0$, $n_A$ и $n_C$. Найдите $\delta$ при $\theta_0=\frac\pi2$, $n_A=2$ и $n_c=1$.

A