
Как показано на рисунке (a), на кремниевую подложку с помощью специальной технологии нанесена тонкая плёнка нитрида галлия постоянной толщины.
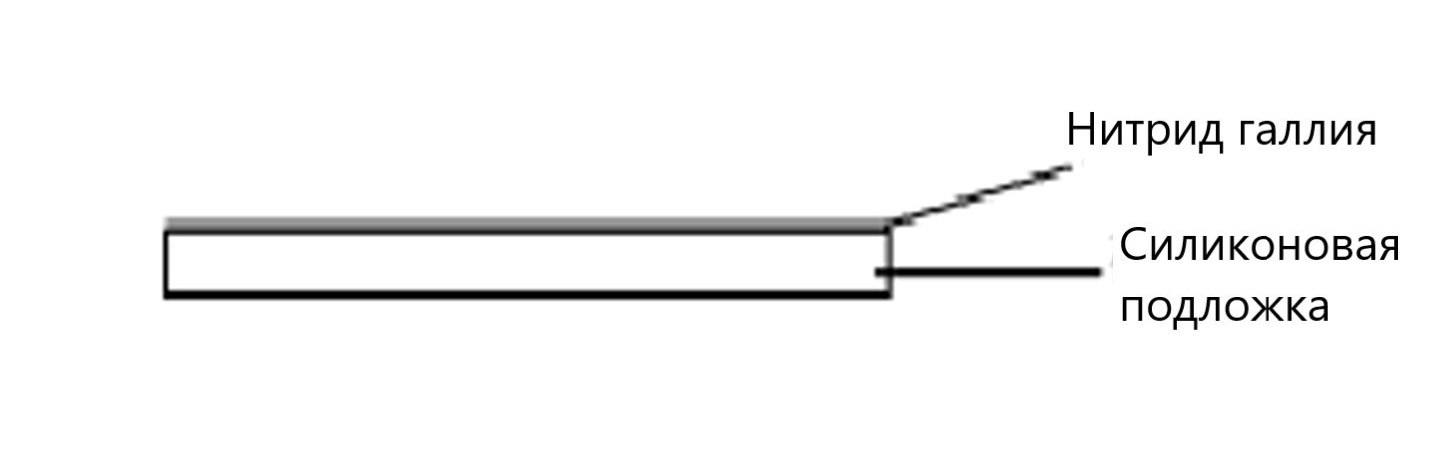
Когда поверхность нитрида галлия облучается равномерно нормально падающим светом в диапазоне длин волн $450\sim1200~\text{нм}$, наблюдается, что спектр отражённого света имеет максимумы лишь при двух значениях длины волны, одно из которых $600~\text{нм}$. Дисперсионное соотношение (соотношение между показателем преломления и длиной волны падающего света в вакууме) имеет вид: $$n^2=2.26^2+\frac{330.1^2}{(\lambda - 265.7)^2}.$$
Показатель преломления кремния изменяется в пределах $3.49\sim5.49$ в зависимости от длины волны.
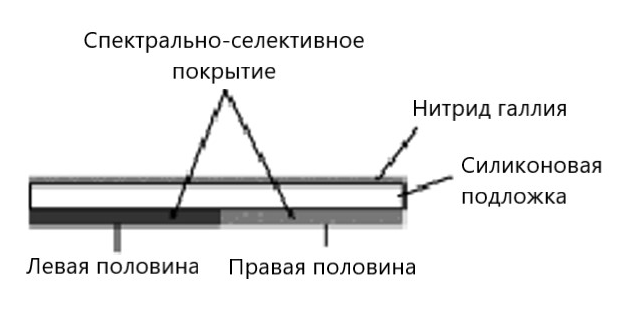
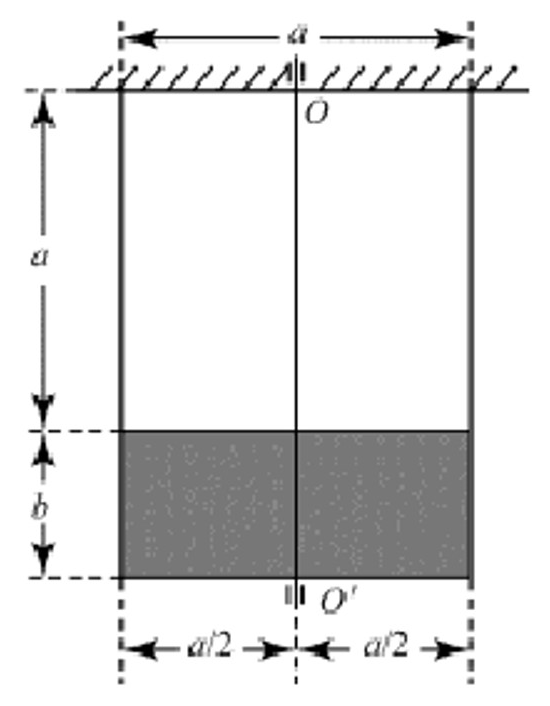
Спектрально-селективное покрытие наносится равномерно на левую и правую половины подложки, как показано на рисунке (b). Известно, что для определённой длины волны света левая половина покрытия полностью поглощает его, а правая полностью отражает. Пусть теперь образец подвешен вертикально с помощью двух лёгких тонких нитей длины $a$. Длина образца равна $a$, а ширина $b$. Он может свободно вращаться вокруг неподвижной вертикальной оси $OO'$, проходящей по его центру, а также перемещаться вверх–вниз, как показано на рисунке (c). В начальный момент времени образец находится в состоянии покоя, и его поверхность облучается лазером необходимой длины волны. При неизменном направлении лазера образец вращается вокруг оси $OO'$ до стабилизации. Считайте, что поверхность образца всё время облучается лазером, действием излучения на боковую поверхность образца пренебрегите. Предположим, что толщина кремниевой подложки равна $d'$, а её плотность равна $\rho'$. Толщина плёнки нитрида галлия равна $d$, его плотность равна $\rho$. Массу покрытия считайте пренебрежимо малой. Диэлектрическая проницаемость вакуума равна $\varepsilon_0$, ускорение свободного падения равно $g$.
Пусть $E = 5.00\cdot10^4~\frac{\text{В}}{\text{м}}$, $d'=3.00\cdot10^{-4}~\text{м}$, $\rho'=2.33\cdot10^3~\frac{\text{кг}}{\text{м}^3}$, $\rho=6.10\cdot10^3~\frac{\text{кг}}{\text{м}^3}$, $\varepsilon_0=8.85\cdot10^{-12}~\frac{\text{Ф}}{\text{м}}$, $g=9.80~\frac{\text{м}}{\text{с}^2}$.