
В обычной жизни нам кажется, что лучи света в окружающей нас атмосфере движутся прямолинейно. Однако это не так, и эффекты искривления лучей незаметны лишь потому, что коэффициент преломления воздуха практически неотличим от единицы. На больших масштабах и при возникновении некоторых атмосферных явлений ей уже нельзя будет пренебречь. В атмосфере Земли примером таких явлений может служить мираж, а в атмосферах других планет — к примеру, Венеры, — практически неограниченное расстояние до горизонта. В этой задаче мы подробно рассмотрим каждое из этих явлений.
Миражи возникают при большом перепаде температур между поверхностью земли и атмосферой. Одним из их многочисленных примеров являются Курильские острова, миражи которых можно наблюдать в Кунаширском проливе в Японии по весне из-за охлаждения воздуха над морем.
Атмосферу можно считать идеальным газом, состоящим из одинаковых молекул массой $m$. Известно, что для большинства газов, в том числе и газа в атмосфере, применима следующая формула для зависимости показателя преломления $n$ атмосферного воздуха:\[n^2-1=\alpha N,\] где $N$ — концентрация молекул, а $\alpha$ — коэффициент, зависящий от природы газа.
При решении задачи считайте, что поверхность воды горизонтальна. Температура атмосферы $T$ повышается с увеличением высоты $h$ над уровнем моря, меняется также и показатель преломления воздуха. Влиянием гравитации пренебрегите, считая атмосферное давление равным $p_0=1~\text{атм}$ вне зависимости от высоты. Показатель преломления атмосферы при нормальных условиях ($T_0=273~\text{К}$, $p_0=1~\text{атм}$) равен $n=1.00028$. Считайте, что температура и показатель преломления зависят только от $h$. Рассмотрим закон Снеллиуса для лучей, испускаемым под углом $\theta_S$ с поверхности земли.
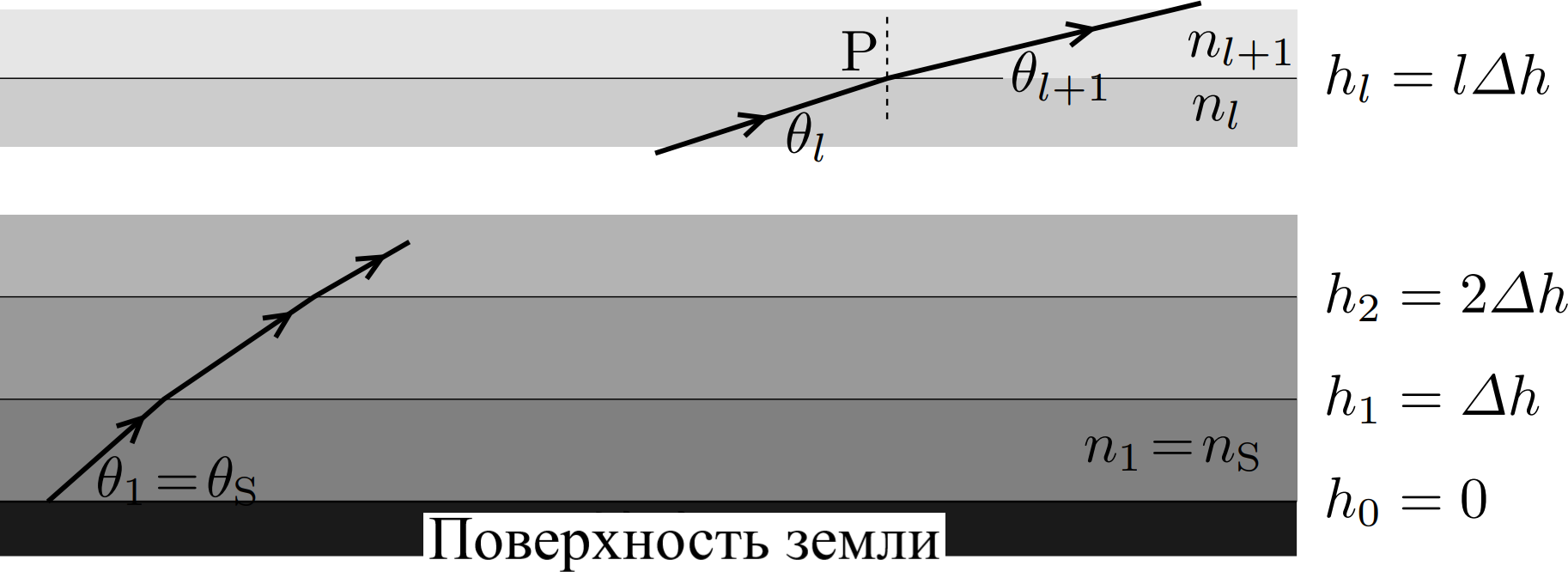
Разделим атмосферу на тонкие слои толщиной $\Delta h$, как показано на рисунке 1. Будем считать, что показатель преломления атмосферы на высоте от $\Delta h(l-1)$ до $\Delta hl$ постоянен и равен $n_l$, а угол между лучом света и горизонтом на этой высоте $\theta_l$, где $l=1,2,3,\ldots$. Показатель преломления атмосферы на поверхности равен $n_1=n_S$.
Предположим, что температура $T(h)$ возрастает линейно с $h$ в диапазоне $0\leq h\leq H$ и постоянна при $h > H$:\[T(h)=\begin{cases}T_S+(T_\mathrm H-T_\mathrm S)\frac hH&0\leq h\leq H\\T_\mathrm H&H < h\end{cases},\]где $T_\mathrm S=T(0) < T_\mathrm H=T(H)$.
Учитывая, что $\frac{T_H-T_S}{T_S}\ll1$, зависимость концентрации $N(h)$ на высоте $h$ ($0 < h < H$) при этом можно также с хорошей точностью считать линейной, т.е.:\[\frac{N(h)}{N_\mathrm S}=1-\frac{N_\mathrm S-N_\mathrm H}{N_\mathrm S}\frac hH,\]где $N_\mathrm S=N(0)$, $N_\mathrm H=N(H)$.
Рассмотрим траекторию луча, испущенного под углом $\theta_\mathrm S$ к горизонту. Будем считать, что по достижении верхней точки траектории $h_\mathrm m(\le H)$ луч начинает двигаться обратно вниз. Направим ось $x$ горизонтально в плоскости распространения луча, тогда его траектория $h(x)$ должна удовлетворять дифференциальному уравнению:\[\frac{\mathrm dh}{\mathrm dx}=\operatorname{tg}\theta=\pm\sqrt{\frac1{\cos^2\theta}-1},\]причём знак $+$ соответствует подъёму, а $-$ — опусканию луча.
С учётом сказанного выше, уравнение для определения траектории луча можно записать в виде\[\frac{\mathrm dh}{\mathrm dx}=\sqrt{a\left(1-\frac hb\right)},\quad a=a_\mathrm m\frac{h_\mathrm m}H.\]
Известно, что решение этого уравнения для луча, проходящего через начало координат $(x,h)=(0,0)$, представляет собой параболу\[h=cx+dx^2.\]
Пусть даны численные значения $T_\mathrm S=275~\text{К}$, $T_\mathrm H=290~\text{К}$, $H=20~\text{м}$. Наблюдатель находится на японском берегу ($h=0$) и наблюдает Курильские острова над поверхностью воды.
Пусть расстояние до островов равно $L$. Наблюдатель видит их под тем же углом, под которым видел бы острова, находись они на том же расстоянии на высоте $h_\mathrm g$ над поверхностью воды.
Как и в части $\bf A$, будем считать, что показатель преломления на высоте $h$ равен $n(h)$, а угол с горизонтом, под которым луч движется на высоте $h$, обозначим как $\theta(h)$. Кривизной земной поверхности можно пренебречь.
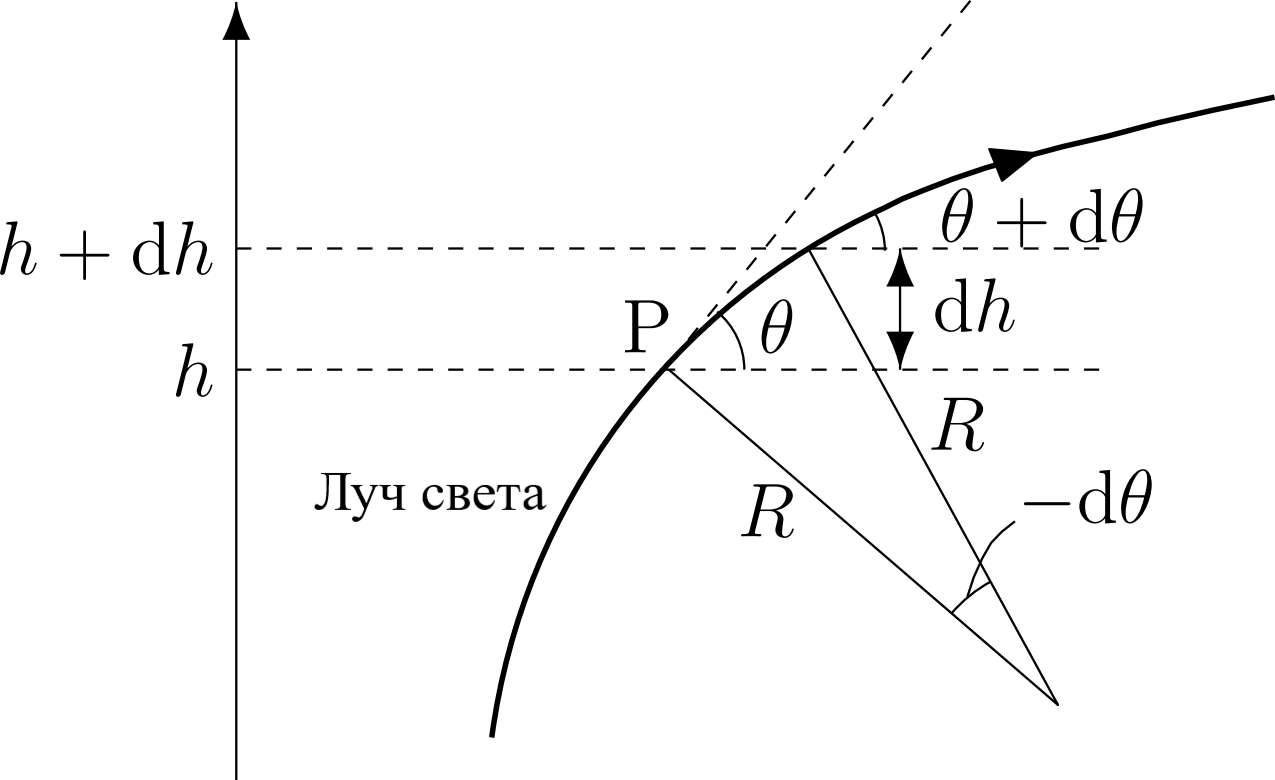
Траектория луча в атмосфере представляет собой кривую, которую в каждой точке можно приблизить участком окружности радиуса $R$. Это значение $R$ называется радиусом кривизны траектории луча в этой точке (см. рисунок 3).
Учтём теперь кривизну Земли. Её радиус $R_\mathrm E=6.4\cdot10^3~\text{км}$. Остальные численные значения $m=29\cdot1.66\cdot10^{-27}~\text{кг}$, $T=300~\text{К}$, $k_\mathrm B=1.38\cdot10^{-23}~\frac{\text{Дж}}{\text{К}}$, $g=9.8~\frac{\text{м}}{\text{с}^2}$.
Атмосфера Венеры состоит из $\mathrm{CO_2}$, который можно считать идеальным и для которого можно применить все полученные выше результаты. Атмосферное давление на поверхности Венеры $p_\mathrm V=93~\text{атм}$ ($1~\text{атм}=1.0\cdot10^5~\text{Па}$), а температура $T_\mathrm V=740~\text{К}$. Радиус Венеры $R_\mathrm V=6.0\cdot10^3~\text{км}$, ускорение свободного падения на её поверхности $g_\mathrm V=8.9~\frac{\text{м}}{\text{с}^2}$, масса молекулы $\mathrm{CO_2}$ $m_\mathrm C=44\cdot1.66\cdot10^{-27}~\text{кг}$. Для показателя преломления на Венере справедливо уравнение:\[n^2=1+\alpha_VN\]с коэффициентом $\alpha_\mathrm V=4\pi a_\mathrm C^3$, где $a_\mathrm C=1.4\cdot10^{-10}~\text{м}$ — эффективный размер молекулы $\mathrm{CO_2}$.