Часть A. Один маятник (2.9 балла)

В этой части мы рассмотрим математический маятник — груз массы $m$, подвешенный на нити длины $l$. Ускорение свободного падения $g$. Угловую амплитуду колебаний маятника обозначим $\alpha$ и будем всюду считать малой $\alpha \ll 1$.

A1  ^0.50 Найдите среднюю за период силу натяжения нити маятника $\langle T\rangle$. Выразите ответ через угловую амплитуду колебаний $\alpha$ и параметры маятника.

A2  ^0.20 Пусть теперь длину нити маятника медленно изменяют, так что относительное изменение длины за один период колебаний мало. Какая работа совершится над грузом, если длина нити изменяется на $\Delta l \ll l$? Выразите ответ через угловую амплитуду колебаний $\alpha$ (считая ее постоянной) и параметры маятника.

A3  ^0.80 В начальный момент времени длина равна $l_0$, а энергия колебаний $W_0$. Найдите энергию колебаний $W_1$, когда длина нити станет равной $l_1$. Потенциальная энергия при этом все время отсчитывается от нижнего положения груза, то есть с изменением длины нити нуль потенциальной энергии смещается!

A4  ^0.40 В условиях предыдущего пункта, найдите амплитуду $\alpha_1$, когда длина маятника станет равна $l_1$. В начальный момент времени длина нити равна $l_0$, амплитуда колебаний $\alpha_0$.

A5  ^1.00 Пусть теперь маятник имеет заряд $q >0$ и помещен во внешнее электрическое поле $E$, направленное вертикально ($E>0$ когда поле направлено вниз). Это электрическое поле медленно меняется со временем. Пусть в начальный момент времени поле было равно нулю, а амплитуда колебаний груза $\alpha_0$. Рассмотрите эту систему аналогично пунктам A1 - A4. Найдите амплитуду колебаний груза $\alpha_2$, когда электрическое поле станет равным $E_1$. Считайте, что поле меняется достаточно медленно, так что изменение амплитуды колебаний за один период мало. Длина маятника постоянна и равна $l$.

Часть B. Два маятника (4.2 балла)

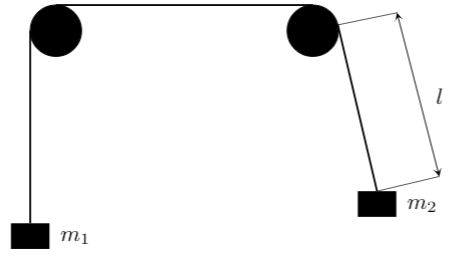
Пусть нить перекинута через два гладких гвоздя малого диаметра, на концах нити закреплены грузы массами $m_1$ и $m_2$ соответственно. При этом левый груз 1 всегда движется строго вертикально, а правый в начальный момент отклоняют на малый угол $\alpha \ll 1$ от вертикали. Нить достаточно длинна, чтобы в процессе движения левый груз не достиг гвоздя. Начальная длина правого участка нити равна $l$. Мы исследуем дальнейшее движение системы с такими начальными условиями при разных предположениях относительно масс грузов.

B1  ^0.90 Пусть $m_1 = m + \delta m$, $m_2 = m$, $\delta m \ll m$. Начальная скорость груза $m_1$ равна нулю, начальная амплитуда колебаний второго груза равна $\alpha_0$, длина правого участка нити $l_0$.
Найдите среднее ускорение $a_0$ левого груза в начальный момент времени. Усреднение производится по периоду колебаний правого груза. Считайте что $a_0 >0$ если ускорение направлено вверх.

B2  ^0.20 При каком значении $\delta m_0$ левый груз в среднем не будет двигаться?

B3  ^1.00 Пусть $\delta m = \delta m_0$. Найдите максимальное смещение $z_{max}$ груза $m_1$ относительно начального положения.

B4  ^1.30 Если значение $\delta m$ не очень сильно отличается от $\delta m_0$, то груз $m_1$ будет совершать колебания, циклическая частота колебаний которых много меньше частоты колебаний правого груза. Найдите эту частоту $\Omega$, а также амплитуду $B$ колебаний. При каких значениях $\Delta m = \delta m - \delta m_0$ такие колебания можно считать гармоническими?

B5  ^0.80 Пусть теперь значение $\delta m \ll m$ произвольно. Найдите максимальную и минимальную длины правого участка нити при дальнейшем движении.

Часть С. Электрическая цепь (0.9 балла)

С1  ^0.90 Рассмотрим колебательный контур, состоящий из катушки индуктивности $L$ и плоского конденсатора, между обкладками которого вакуум. Расстояние между обкладками конденсатора медленно меняют. Пусть начальная емкость конденсатора $C_0$, начальная амплитуда тока в контуре $I_0$. Рассмотрите систему аналогично пунктам A1-A4. Найдите амплитуду тока $I_1$ в тот момент, когда емкость конденсатора станет равна $C_1$.