
Исследования человеческого зрения и разработка технологий фотографирования неизбежно связаны с изучением фокусировки изображений с помощью собирающих линз.
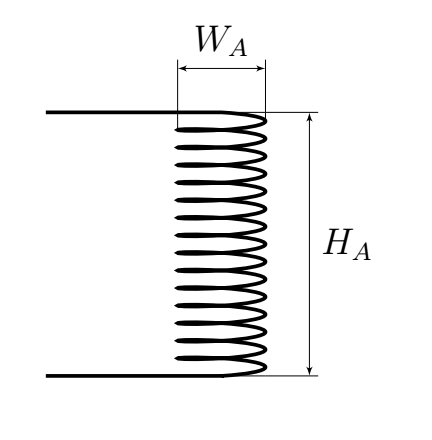
В данной работе источником света выступает спираль внутри лампы накаливания. Обозначим ее диаметр за $W_A$, высоту за $H_A$ а количество витков за $N_A$.
Внимание! В задаче не требуется оценка погрешностей.
Внимание! Пользуйтесь индивидуальной лампой для освещения рабочего места.
Оборудование:
Внимание! Самостоятельно не доставайте провода лампы из клемм источника постоянного напряжения.
Для питания лампы используйте источник постоянного напряжения $U=9.0~\text{В}$. При корректной работе лампы у нее светится только спираль накаливания (при некорректной внутренняя поверхность покрывается светлым осадком, и поэтому лампочка «светится» полностью).
Располагайте лампу так, чтобы спираль накаливания была вериткальной.

Обозначения, выбранные в этой части, справедливы в течение всей последующей задачи.
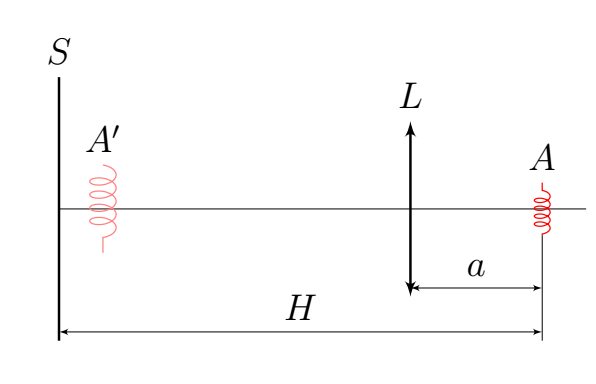
Рассмотрим оптическую схему, состоящую из неточечного источника $A$, линзы $L$ и экрана $S$. На рисунке за $A'$ обозначено изображение источника $A$.
В простейшем фотоаппарате вместо экрана $S$ используется матрица из фоточувствительных элементов, например, фотодиодов.
За $L_F$ обозначим линзу с бóльшим фокусным расстоянием, а само фокусное расстояние за $F$. Линзу с меньшим фокусным расстоянием соответственно $L_f$, ее фокусное расстояние $f$.
При достаточно больших $H$ на экране получается сфокусировать изображение при двух положениях: ближняя фокусировка — положение при меньшем $a$ и дальняя фокусировка — положение при бóльших $a$.
Метод определения фокусного расстояния линзы, рассмотренный в пункте $\textbf{A1}$ в любом случае имеет существенный недостаток: нет формального критерия «сфокусированного изображения». В данной части мы дополним метод и избавим его от этого недостатка, рассмотрев физику неточной фокусировки и понятие резкости.
В данной части используется только линза $L_F$. Расстояние $H \approx 1.20~\text{м}$.
За $a_0$ обозначим расстояние $a$, соответствующее ближней фокусировке. Меняя расстояние $a$ в окрестности $a_0$, можно получать на экране изображения разной степени размытости (примеры чёткого и очень нечёткого изображения приведены на фотографиях ниже). Также на размытость изображения влияет форма и диаметр диафрагмы — экрана с отверстием, которым закрывают часть линзы.
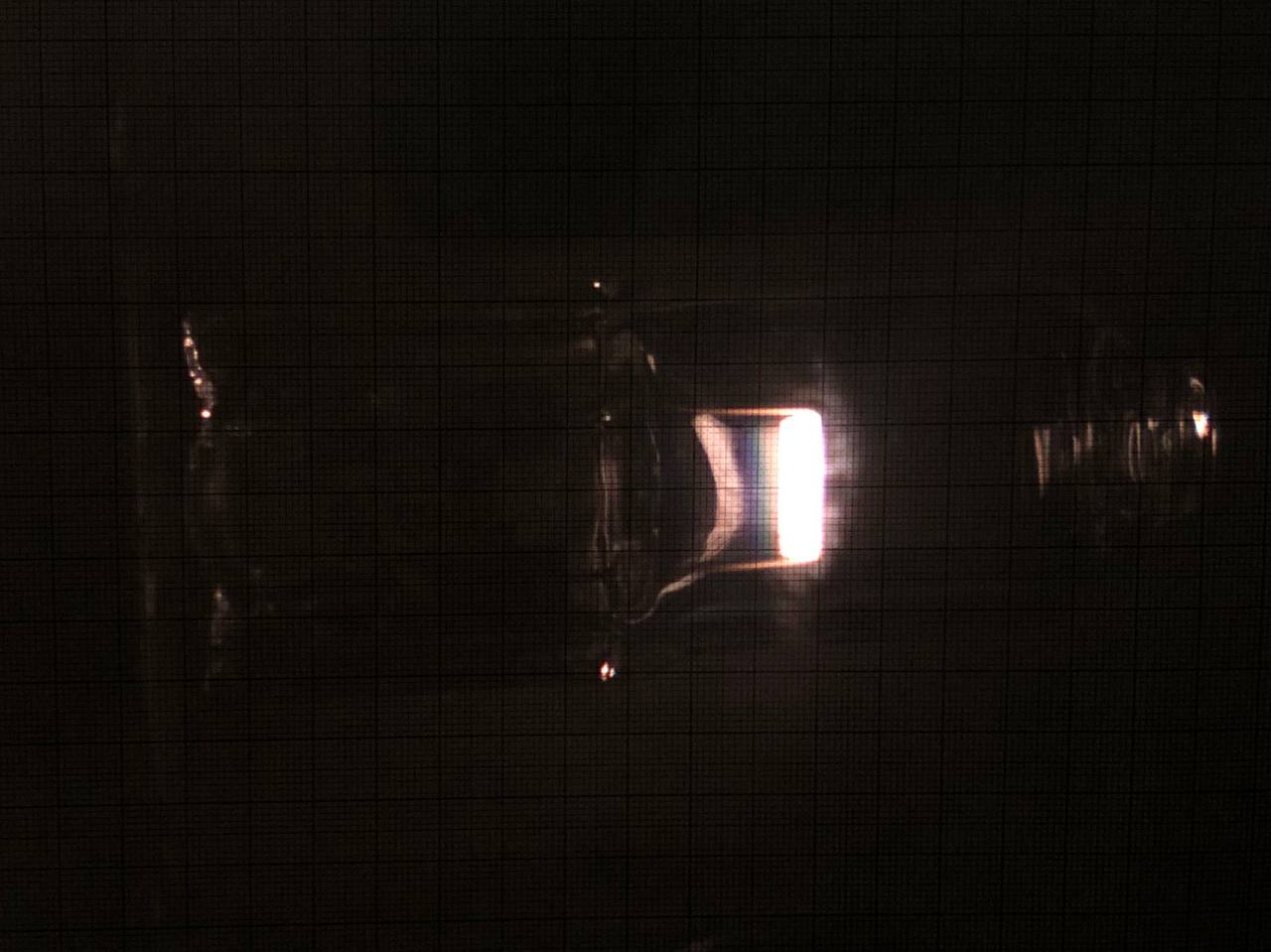

B1
0.20
Выставьте линзу так, что $a = a_0 + F/2$. В дальнейших пунктах мы будем изучать характерный размер таких изображений, поэтому выберите, какой линейный размер — высоту $h$ или ширину $w$ нечеткого изображения вы будете измерять в последующих пунктах. Обоснуйте свой выбор и крестиком обозначьте его в листе ответов. Этот размер будет обозначаться за $p$.
В первую очередь изучим влияние диафрагмы на размытость.
Теперь посмотрим, как ошибка фокусировки влияет на размытость.
Теперь изучим, как форма даже несфокусированного изображения связана с формой источника.
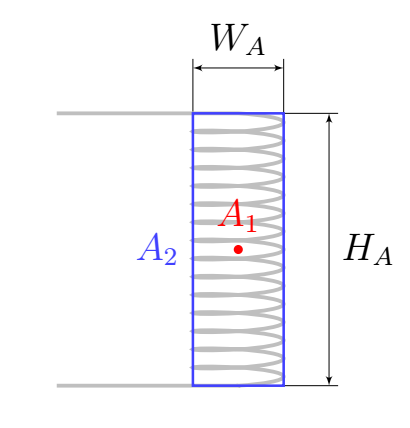
Границу нечеткого изображения лампы невозможно точно описать без рассмотрения распределения интенсивности света по экрану, поэтому для начала рассмотрим две упрощенные модели источника света:
Наша задача заключается в «совмещении» этих моделей. Пусть «совмещенный» источник создает границу изображения $\Gamma$. Каждой конкретной точке $\Gamma$ соответствует луч $B'$ выходящий из центра изображения, и проходящий через нее. Будем считать, что точка границы $\Gamma$ находится посередине между точками $\Gamma_1 \cap B'$ и $\Gamma_2 \cap B'$ .
В данной части используются обе линзы. Расстояние $H \approx 1.20~\text{м}$.
Меняя $a$ в окрестности $a_0$ в части $\textbf{B}$ вы, вероятно, заметили, что граница изображения имеет различный цвет при $a < a_0$ и $a > a_0$. Это связано с тем, что разные цвета немного по-разному преломляются в стекле, из которого сделана линза, а описать это можно в терминах разных показателей преломления для света разного цвета: $n_\text{b}$ для синего и $n_\text{r}$ для красного.
$L_F$ Граница синяя при $a < a_0$, красная при $a > a_0$ $L_F$ Граница красная при $a < a_0$, синяя при $a > a_0$ $L_f$ Граница синяя при $a < a_0$, красная при $a > a_0$ $L_f$ Граница красная при $a < a_0$, синяя при $a > a_0$
$L_F$ $n_\text{b} > n_\text{r}$ $L_F$ $n_\text{r} > n_\text{b}$ $L_f$ $n_\text{b} > n_\text{r}$ $L_f$ $n_\text{r} > n_\text{b}$
В данной части задачи используется только линза $L_F$.
В данной части используются обе линзы, а $H\approx1.20~\text{м}$. С помощью системы из двух линз получите четкое изображение источника $A$ на экране $S$.
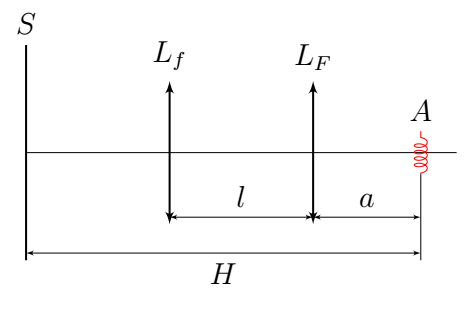
E1
0.85
При различных фиксированных значениях $a$ подберите расстояния $l$, соответствующие четкому изображению. Измерьте высоту четкого изображения $h$. Если при нескольких разных значениях $l$ получается несколько четких изображений, то выбирайте изображение, имеющее большее $h$. У зависимости $h$ от $a$ есть характерная точка, опишите ее и промерьте ее окрестность особенно тщательно. Всего сделайте не менее 15-ти измерений.
В силу того, что любая реальная линза не является тонкой, фокусное расстояние для лучей идущих далеко от оптической оси отличается от фокусного расстояния для параксиальных лучей.
Заметен этот эффект (наряду с хроматической аберрацией) в телескопе Кеплера — системе из двух собирающих линз, отдаленных друг от друга на расстояние, близкое к сумме их фокусных расстояний.
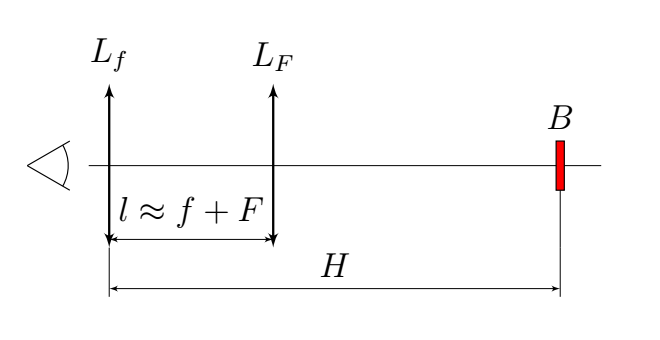
Расположите две линзы на расстоянии $l \approx f+F$ рядом друг с другом у одного из краев стола, чтобы вы могли через них наблюдать за предметами, расположенными с другого края — там закрепите линейку в штативе и расположите источник света так, чтобы он освещал линейку $B$, но не светил в линзы.
Увеличением телескопа называется отношение видимого размера объекта к настоящему размеру объекта.
E3
0.80
Настройте телескоп Кеплера так, чтобы расстояние между линзой $L_f$ и линейкой было $H\approx1.20~\text{м}$, и через телескоп Вам было четко видно увеличенное изображение линейки. Сделайте необходимые измерения и рассчитайте экспериментальное значение увеличения $\Gamma_K$ телескопа Кеплера в такой системе.