1  ^1.50 Землю можно считать однородным шаром радиуса $6370~\text{км}$, ускорение свободного падения на поверхности которого равно $g_0=9.80~\frac{\text{м}}{\text{с}^2}$ (эффектами вращения Земли пренебрегите). Предположим, что под землёй на глубине $15~\text{км}$ образовалось шарообразное озеро $20~\text{км}$ в диаметре, заполненное водой. Найдите, на какую величину $\Delta g$ изменится ускорение свободного падения на поверхности земли непосредственно над озером. Универсальная гравитационная постоянная равна $G=6.67\cdot10^{-11}~\frac{\text{Н}\cdot\text{м}^2}{\text{кг}^2}$, плотность воды $\rho_{\text{в.}}=1.0\cdot10^3~\frac{\text{кг}}{\text{м}^3}$.

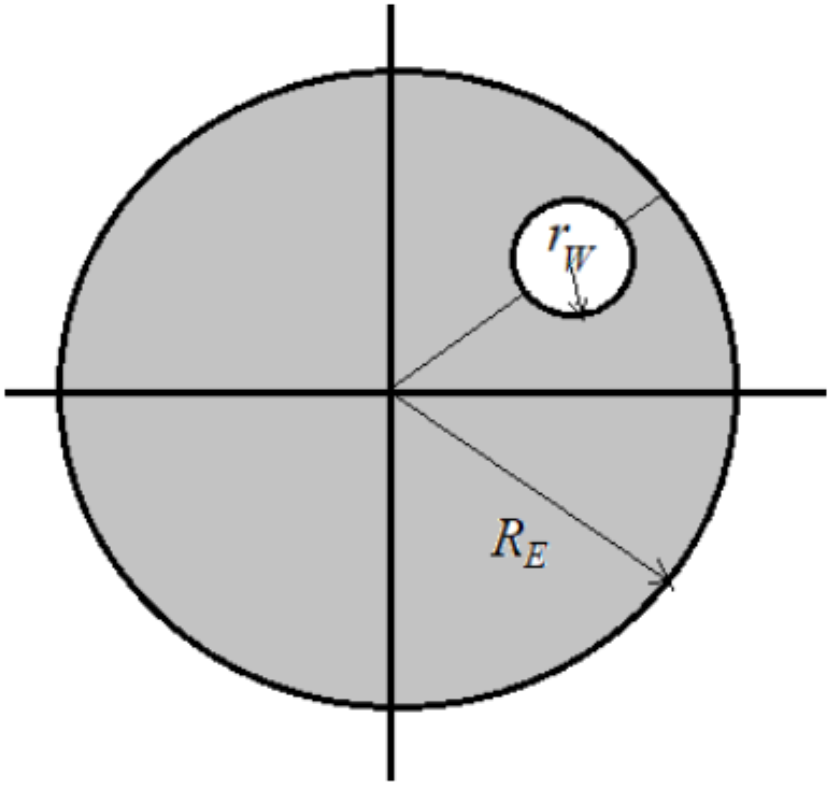
\[\implies\Delta g=\cfrac{4\pi Gr_w^3}{3d^2}[\rho_0-\rho_w]=5.60\cdot10^{-3}~м/с^2=5.71\cdot10^{-4} g_0\]

2.1  ^2.00 Найдите коэффициенты $B_0$ и $\beta$.

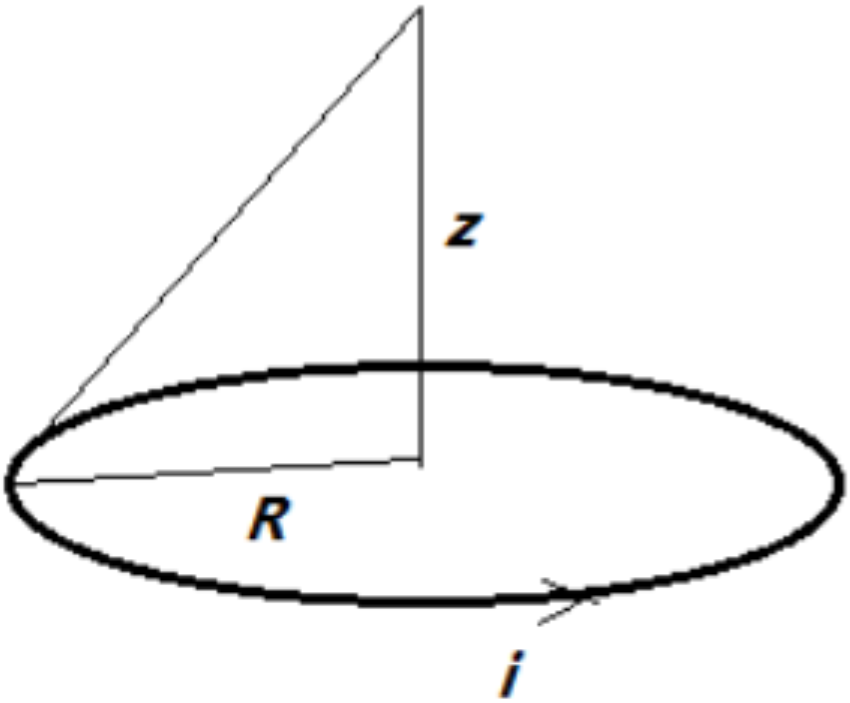
\[=\cfrac{\mu_0Ni_0}{2R}\left(\alpha+\cfrac1{2\sqrt2}\right)\left[1-\cfrac{3}{2R(1+2\sqrt2\alpha)}(z-R)\right]=B_0[1-\beta(z-R)]\implies\]

2.2  ^1.00 Найдите ток $I_0$, индуцированный в кольце в положении равновесия $z=R$.

Поскольку сопротивление сверхпроводящего кольца равно нулю, магнитный поток через него будет оставаться постоянным, а ток в кольце будет подстраиваться, чтобы уравновесить изменение внешнего поля. Таким образом, если в кольце течёт ток $I_0$, можно записать:\[\Phi=B_z\big|_{z=R}\cfrac{\pi D^2}4+LI_0=\operatorname{const}\]Учитывая начальные условия $t=0$, $z=0$, $I=0$, $\Phi=0$,\[LI_0=-\pi B_0D^2/4\implies I_0=-\cfrac1{4L}\pi D^2B_0\implies\]

2.3  ^1.00 Найдите ускорение свободного падения $g$ в месте расположения гравиметра.

В положении равновесия сила Ампера должна в точности равняться по величине силе тяжести, действующей на кольцо:

$mg=|I_0|B_r\pi D\implies$
\[\implies g=\cfrac{\cfrac1{4L}\pi D^2B_0\cdot\cfrac12 B_0\cdot\beta\cfrac D2\cdot \pi D}m=\cfrac{\beta\pi^2D^4B_0^2}{16Lm}=\cfrac{\cfrac{3}{2 R(2 \sqrt{2} \alpha+1)} \pi^2 D^4 \cfrac{\mu_0^2 N^2 i_0^2}{4 R^2}\left(\alpha+\cfrac{1}{2 \sqrt{2}}\right)^2}{16 L m} \implies\]

Таким образом, зная параметры кольца и катушек, можно измерять ускорение свободного падения $g$ по равновесному току $i_0$ в кольце

3  ^1.50 Пренебрегая краевыми эффектами, найдите соотношение между $\Delta g$ и~$\Delta V$.

Изначально сверхпроводящее кольцо находится в плоскости верхней катушки $z=R$, и силы, действующие на неё со стороны конденсаторов, уравновешивают друг друга. Действительно, если расстояние между пластинами равно $d$, а расстояние между нижней пластиной и кольцом — $x$, то дополнительная сила на кольцо равна:\[F=\cfrac12\varepsilon_0AV_C^2\left[\cfrac1{(d-x)^2}-\cfrac1{x^2}\right]\]Равновесие достигается при $x=d/2$, когда $F=0$.

Теперь, если ускорение свободного падения изменилось на $\Delta g$, постоянное напряжение на верхней пластине увеличилось на $\Delta V$, а на нижней — уменьшилось на $\Delta V$, то результирующая сила окажется равна:\[F=\cfrac12\varepsilon_0A\left[\cfrac{(V_C+\Delta V)^2}{(d-x)^2}-\cfrac{(V_C-\Delta V)^2}{x^2}\right]\]Поскольку для балансировки моста нужно $C_1=C_2$, кольцо должно остаться в равновесии в положении $x=d/2$, где результирующая сила, действующая на него со стороны пластин, будет равна:\[F\approx\cfrac12\cfrac{\varepsilon_0A}{d^2/4}4V_C\Delta V=\cfrac{8\varepsilon_0A}{d^2}V_C\Delta V\]С другой стороны, эта сила должна быть равна $F=m\Delta g$, чтобы скомпенсировать изменение силы тяжести. Отсюда получаем соотношение между $\Delta g$ и $\Delta V$: