
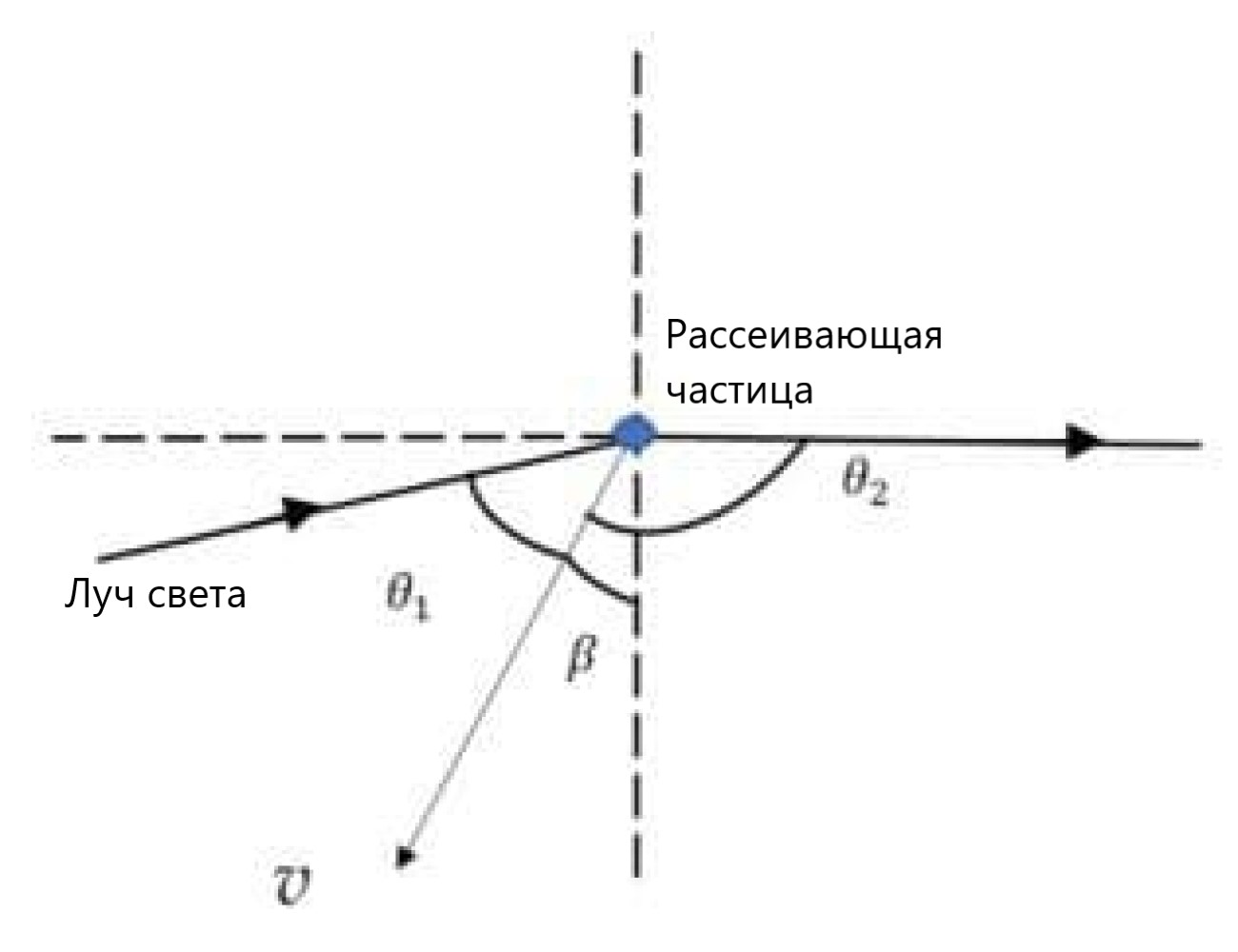
В 1964 году учёные Е и Камминс пронаблюдали эффект Доплера у света, рассеянного на частицах в потоке воды. С тех пор лазерная доплеровская анемометрия стала широко использоваться. Чтобы получить рассеянный свет достаточной интенсивности, в жидкость добавляют рассеивающие частицы соответствующих размеров и концентрации. Рассеяние происходит при облучении лазером движущихся частиц и может дать информацию о скорости их движения (и скорости движения жидкости соответственно). Угол между скоростью частицы $v$ и вертикалью равен $\beta$.
1
10.00
Как показано на рисунке (a), луч света частотой $f$ рассеивается движущейся в жидкости частицей. Скорость распространения света в среде равна $\frac{c}{n}$ (где $n$ — коэффициент преломления жидкости), а частицы движутся со скоростью $v$ ($v\ll\frac{c}{n}$). Угол между направлением распространения падающего света и скоростью частицы равен $\theta_1$, направлением распространения рассеянного света — $\theta_2$. Найдите, как зависит изменение частоты $\Delta f$ света при рассеянии от направления распространения рассеянного света. Если скорость частицы $v\sim1~\frac{\text{м}}{\text{с}}$ и частота света $f\sim10^{14}~\text{Гц}$, можно ли использовать спектрометр с разрешением $5~\text{МГц}$ для обнаружения эффекта Доплера?
2
14.00
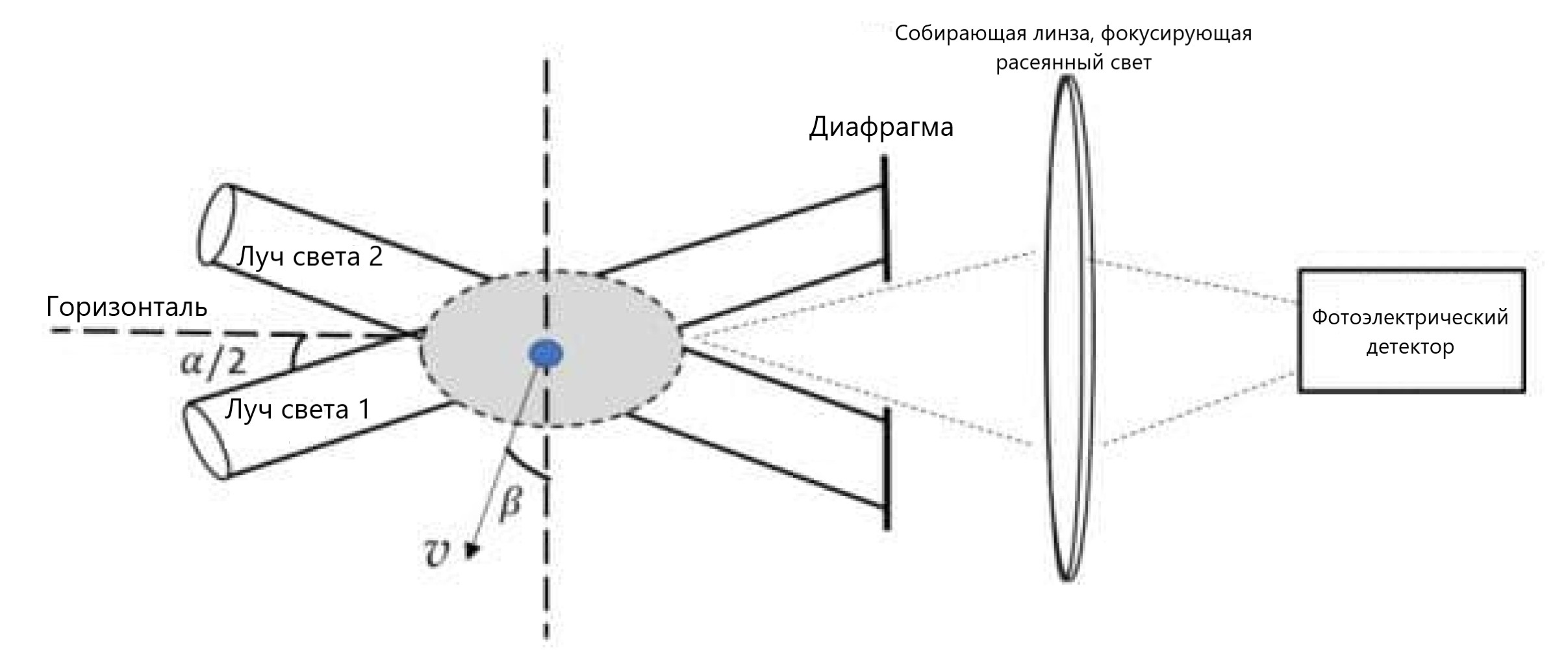
Как показано на рисунке (b), два нерасходящихся когерентных луча частоты $f$, направления распространения которых лежат в одной вертикальной плоскости, используются для облучения одной и той же частицы в жидкости, причём угол между каждым из лучей и горизонталью равен $\frac{\alpha}{2}$ (считайте$\alpha$ достаточно малым). По достижении фотодетектора фазы рассеянного света равны $\varphi_1$ и $\varphi_2$ соответственно. Направления вектора напряжённости электрического поля лучей почти одинаковы, их амплитуда равна $E_0$. Величина тока детектора пропорциональна интенсивности попадающего в него света с коэффициентом пропорциональности $k$. Считая, что детектор на выходе рассчитан на переменный ток с частотами в диапазоне $10^2-10^7~\text{Гц}$, найдите выражение, которым этот ток задаётся. Для простоты считайте, что скорость частицы лежит в одной плоскости с направлениями распространения падающих лучей.
3
16.00
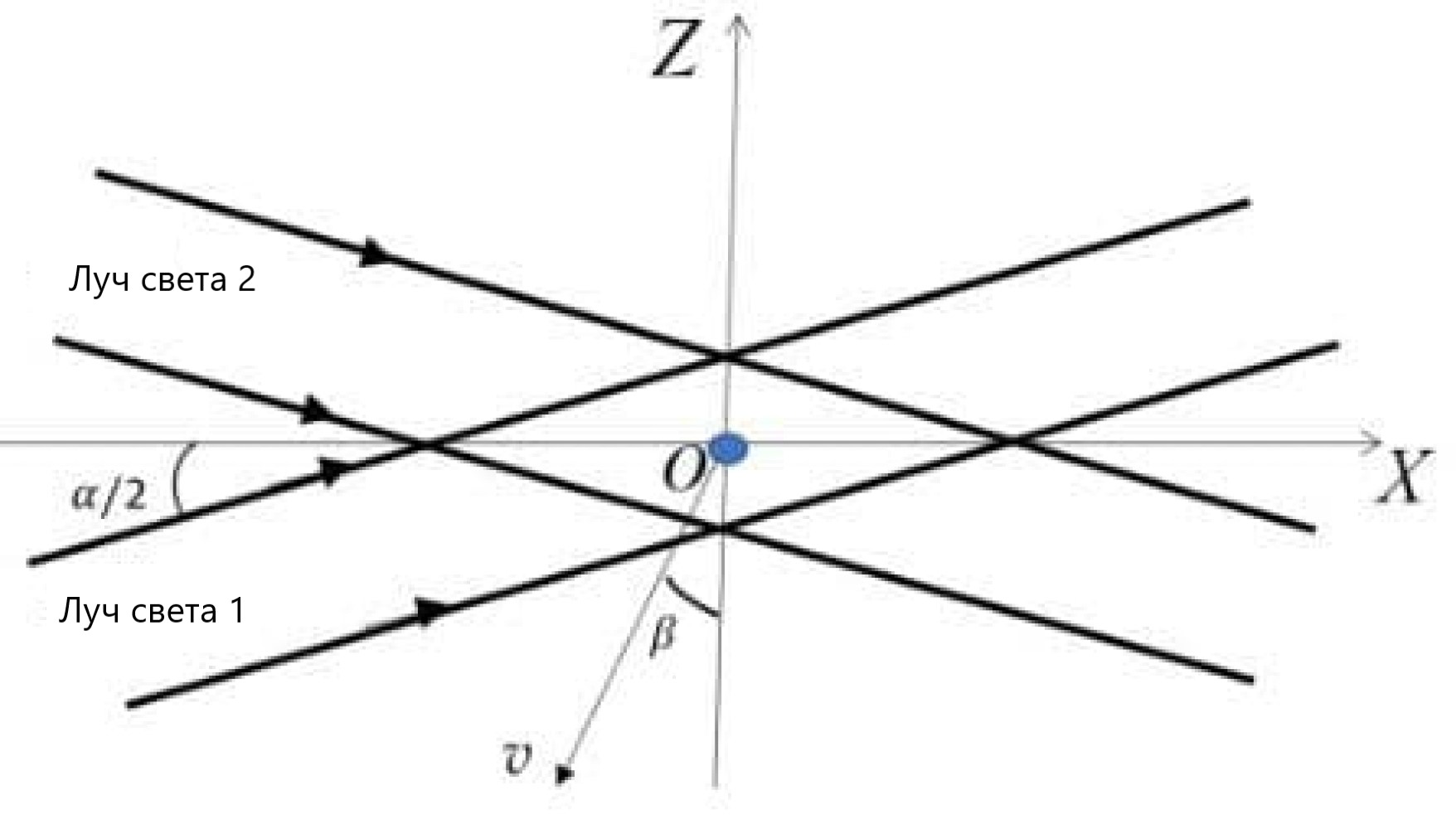
Предположим, что два нерасходящихся когерентных луча распространяются в плоскости $xOz$ симметрично относительно оси $Ox$ и достигают точки пересечения, как показано на рисунке (c). Найдите расстояние $d$ между соседними максимумами получаемой интерференционной картины. Частица (скорость которой также лежит в плоскости $xOz$), рассеивает свет, перемещаясь вдоль интерференционной картины, в результате чего рассеянный свет имеет периодически меняющуюся с некоторой частотой $f_D$ амплитуду. Найдите эту частоту.