1 Найдите кинематическую связь между этими функциями. В ответ могут войти как сами функции, так и их производные по времени.

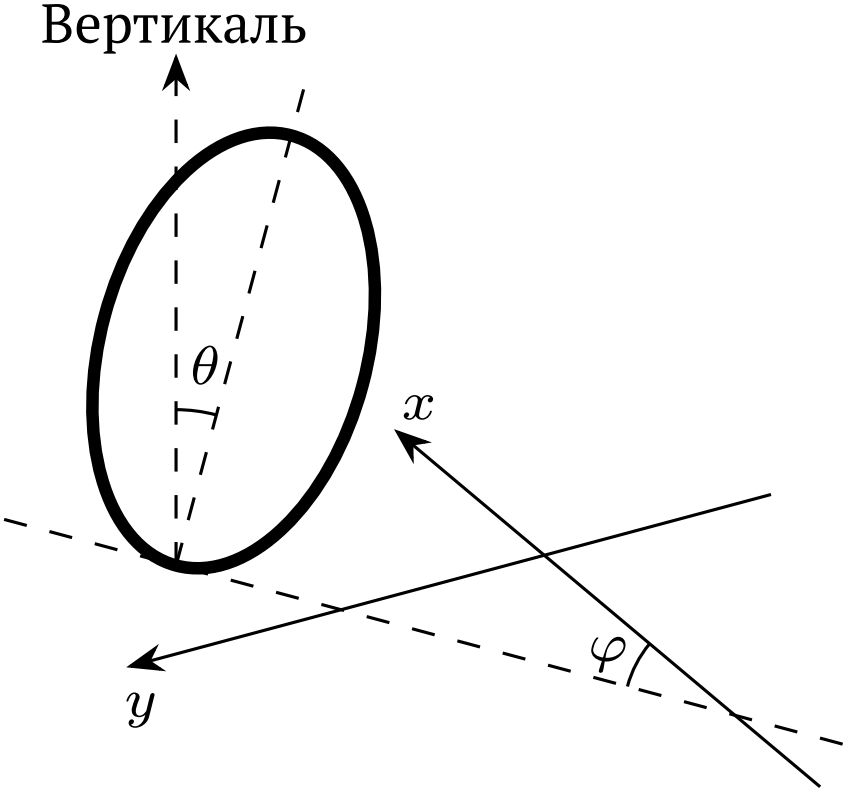
Рассмотрим частный случай равномерного кругового движения колеса, т.е. когда точка его соприкосновения с поверхностью перемещается с постоянной скоростью, описывая окружность радиуса $r$ вокруг вертикальной оси $z$. При этом $\theta(t)=\theta=\operatorname{const}$, а $\varphi(t)$ — линейная функция времени. В лабораторной системе отсчёта $\Sigma$ можно, не умаляя общности, положить:\[\left(\begin{array}cx(t)\\y(t)\end{array}\right)=r\left(\begin{array}c-\sin\omega t\\\cos\omega t\end{array}\right),\]где $\omega$ — угловая скорость, которую ещё предстоит найти. В системе отсчёта $\Sigma'$, вращающейся с угловой скоростью $\omega$ вокруг оси $z$, углы $\theta$ и $\varphi$ постоянны, а колесо вращается вокруг сохраняющей ориентацию оси симметрии. В этой системе отсчёта на каждый участок колеса буду также действовать центробежная сила и сила Кориолиса.

2 Найдите действующие на колесо центробежную силу $\vec F_ц$ и силу Кориолиса $\vec F_К$, а также результирующие моменты этих сил $\vec\tau_ц$ и $\vec\tau_К$ соответственно.

3 Найдите угловую скорость $\omega$ и силу трения $\vec f$, действующую на колесо со стороны поверхности ($\omega$ не должна входить в ответ).

Если же колесо катится с достаточно большой скоростью, вертикальное положение $\theta=0$ может оказаться устойчивым. В этом случае можно считать, что центр масс колеса движется с почти постоянной скоростью $V$ в положительном направлении оси $x$. Тогда в первом приближении можно записать $x(t)=Vt+\delta x(t)$, где $\delta x(t)$ — малая величина, меняющаяся по гармоническому закону с некоторой угловой скоростью $\Omega$ (как и $y(t)$, $\theta(t)$ и $\varphi(t)$).

4 Выведите в первом нетривиальном приближении уравнения движения колеса. Найдите отсюда угловую скорость $\Omega$ и минимальное значение $V_\mathrm{min}$ скорости колеса, при которой вертикальное положение будет устойчивым.