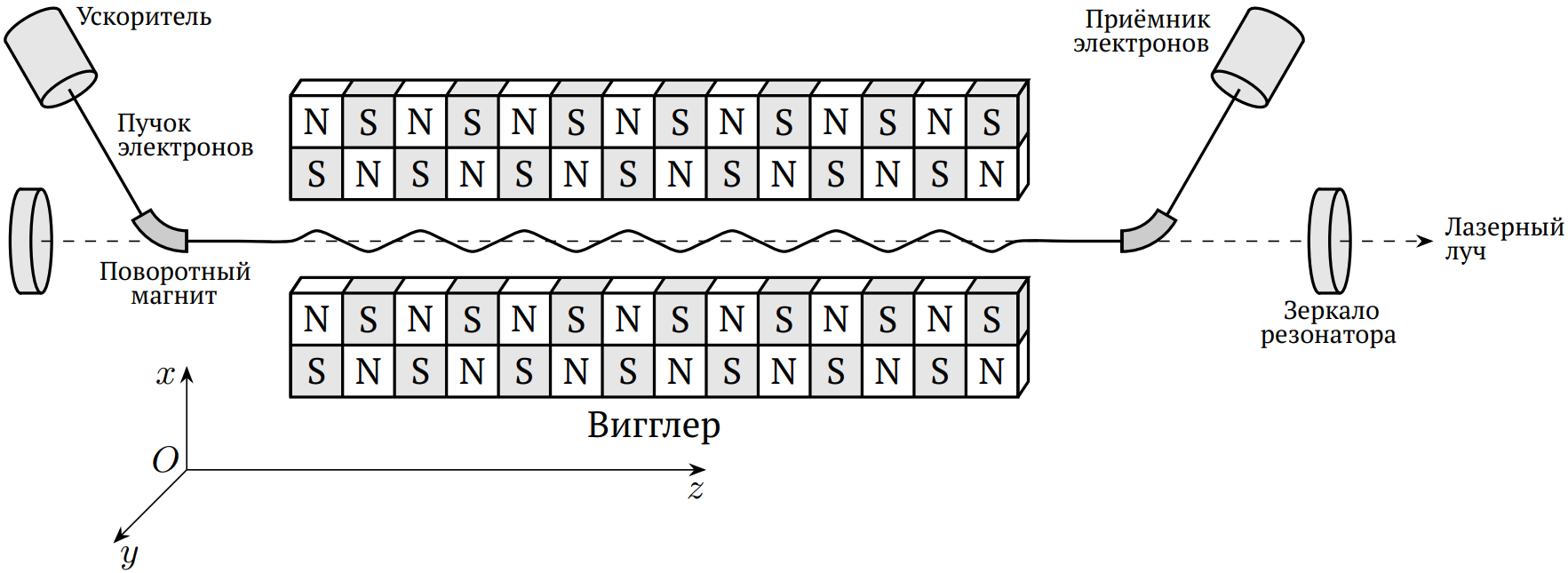
Лазер на свободных электронах — это устройство, преобразующее энергию пучка электронов в когерентное излучение. Эта технология имеет большие перспективы в науке, производстве и других областях. Как показано на рисунке ниже, лазер на свободных электронах состоит из трёх основных частей: ускорителя электронного пучка, вигглера и оптического резонатора. Основная часть — вигглер — состоит из ряда постоянных магнитов, ориентация которых меняется вдоль оси $z$ в пространственным периодом $\Lambda$. Это позволяет создать по оси $x$ постоянное неоднородное магнитное поле\[B=B_0\cos\frac{2\pi z}\Lambda.\]Пучок электронов разгоняется в ускорителе до скорости $v_0$ и с помощью поворотного магнита направляется в вигглер. Под действием магнитного поля вигглера электроны начинают совершать малые колебания по оси $z$, теряя небольшую часть своей энергии на излучение. Масса покоя электрона равна $m_e=9.11\cdot10^{-31}~кг$, его заряд равен $-e$, $e=1.60\cdot10^{-19}~Кл$. Влияние гравитации не учитывайте.
Помимо лабораторной системы отсчёта $S(x,y,z)$ введём систему отсчёта $S'(x',y',z')$, оси которой параллельны осям $S$ и которая движется относительно неё со скоростью $v_0\vec e_z$. В момент попадания электрона в вигглер $(t=t'=0)$ начала координат обеих систем совпадают.
Примечание: считайте известным закон преобразования электромагнитного поля при переходе между системами отсчёта $S$ и $S'$:\[\left\{\begin{array} { l }
{ E _ { x ^ { \prime } } = \dfrac { E _ { x } - v _ { 0 } B _ { y } } { \sqrt { 1 - \left[ \frac { v _ { 0 } } { c } \right] ^ { 2 } } } } \\
{ E _ { y ^ { \prime } } = \dfrac { E _ { y } + v _ { 0 } B _ { x } } { \sqrt { 1 - \left[ \frac { v _ { 0 } } { c } \right] ^ { 2 } } } } \\
{ E _ { z ^ { \prime } } = E _ { z } }
\end{array}\qquad\qquad \left\{\begin{array}{l}
B_{x^{\prime}}=\dfrac{B_x+\frac{v_0}{c^2} E_y}{\sqrt{1-\left[ \frac { v _ { 0 } } { c } \right]^2}} \\
B_{y^{\prime}}=\dfrac{B_y-\frac{v_0}{c^2} E_x}{\sqrt{1-\left[ \frac { v _ { 0 } } { c } \right]^2}} \\
B_{z^{\prime}}=B_z
\end{array}\right.\right.\]где $c=3.00\cdot10^8~\fracмс$ – скорость света в вакууме.