Измерения радиусов звёзд — сложная задача ввиду большого расстояния до них. Неоднородности в атмосфере размывают изображение, затрудняя определение их реального размера. Один из возможных методов измерения радиуса звёзд — использование интерферометра. Этот метод был предложен Майкельсоном и Пизом в 1921 году для измерения диаметра Бетельгейзе.
На рисунке ниже представлена схема интерферометра, использованного для измерения радиуса звезды.

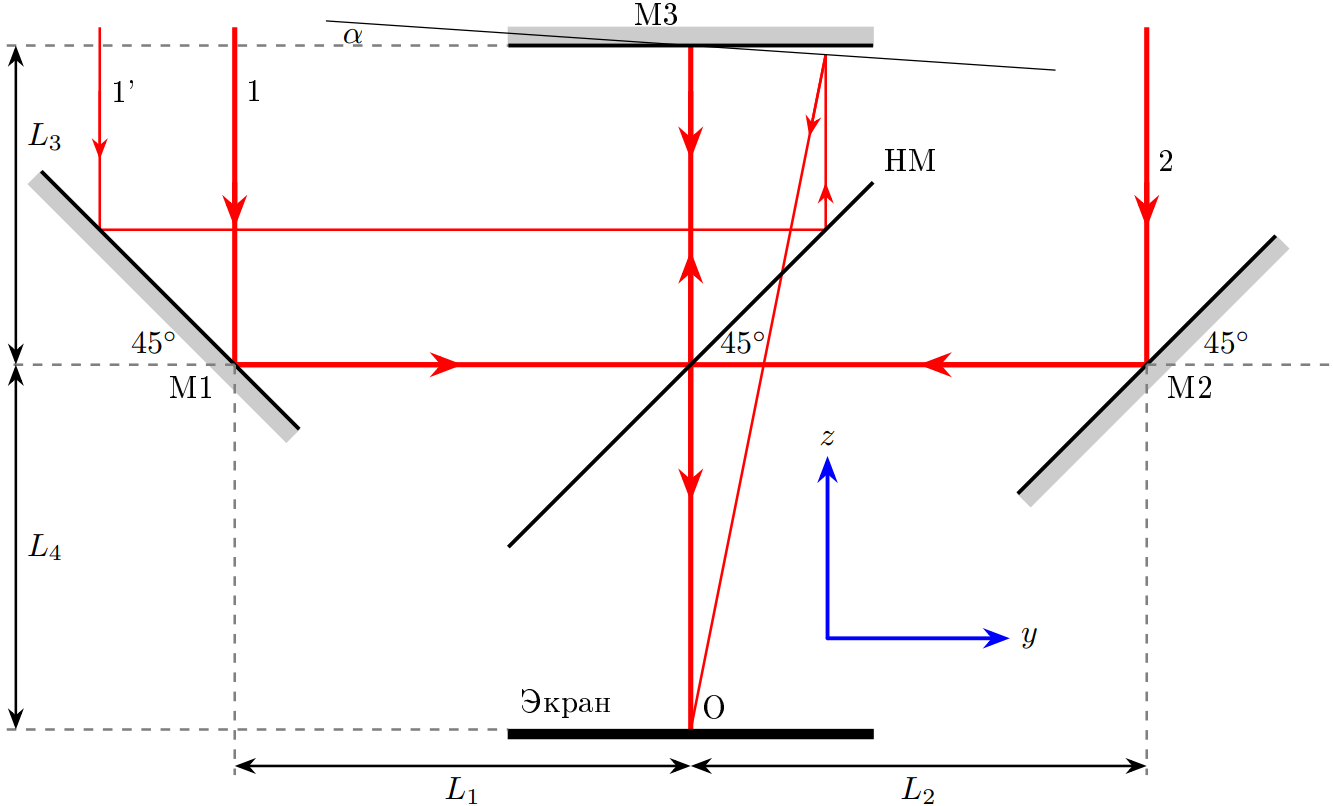
Отражаясь от зеркала M1, луч 1 попадает на светоделитель HM, который отражает $50\%$ света по интенсивности и пропускает остальные $50\%$. Отражённый луч попадает на зеркало M3, отразившись от которого проходит сквозь HM и падает на экран. В это же время луч 2 отражается от зеркала M2. Отразившись от HM, он также попадает на экран. Считайте, что зеркала M1, M2, M3 отражают весь падающий на них свет, добавляя при этом к его фазе $\pi$ радиан. Длина волны используемого света равна $\lambda$.

Часть A. Лучи, параллельные оси $z$ (1.6 балла)

A1 Рассмотрим случай, когда лучи 1 и 2 параллельны оси $z$, а зеркало M3 параллельно плоскости $xy$. Найдите разность оптических путей $\Delta_{12}$ между лучами 1 и 2, если они оба падают на экран в точке $O$.

A S

A2 Рассмотрим случай, когда зеркало M3 отклоняют на угол $\alpha$ от плоскости $xy$ путём вращения вокруг оси $x$ (см. рис. 1). Если луч 1' падает на экран в точке $O$, найдите разность оптических путей $\Delta_{1'2}$ между лучами 1' и 2. Покажите, что в первом приближении разность хода не зависит от $\alpha$ и упростите ваш ответ при $\alpha\ll1$.

A S

Часть B. Лучи под углом $\theta$ в плоскости $yz$ (4.7 балла)

Пусть теперь лучи падают на интерферометр под углом $\theta\ll1$ к оси $z$ в плоскости $yz$, как показано на рисунке ниже. Как и в A2, зеркало M3 отклонено на угол $\alpha$.

Примечание: Далее во всех пунктах задачи работайте только в линейном приближении при вычислении оптический путей, т.е пренебрегайте членами, содержащими множители $\alpha^2$, $\theta^2$, $\alpha\theta$ и т.п

B1 Пусть лучи 1 и 2 падают в фиксированные точки зеркал M1 и M2 соответственно. Покажите в листах решений, что в первом приближении оптические пути лучей 1 и 2 от точек отражения от зеркал M1 и M2 соответственно до экрана не зависят от углов $\theta$ и $\alpha$.

S

B2 Пусть углы $\alpha$ и $\theta$ зафиксированы, а положения точек падения лучей 1 и 2 на зеркала M1 и M2 соответственно могут изменяться. Покажите в листах решений, что оптические пути лучей 1 и 2 от пунктирной линии, соответствующей координате $z_\text{п}=L_3+L_4$ (подразумеваются точки пересечения пунктирной линии с траекториями лучей 1 и 2 до падений на зеркала M1 и M2 соответственно), до экрана в первом приближении не зависят от углов $\theta$ и $\alpha$.

S

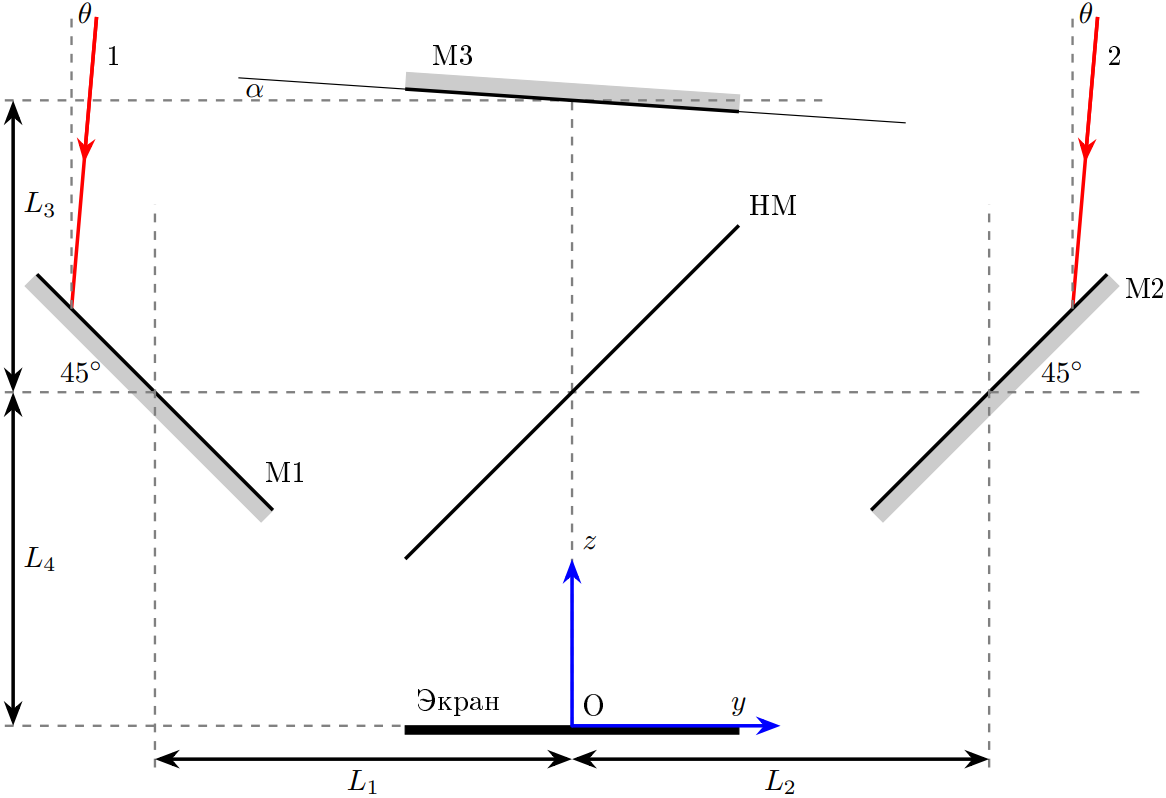
Если лучи 1 и 2 падают на экран в точке $O$, разность фаз между ними может быть записана в виде:\[\delta_{12}=\frac{2\pi}\lambda b\theta+\delta_O.\]

B3 Выразите $b$ и $\delta_O$ через $\lambda$, $L_1$, $L_2$, $L_3$, $L_4$.

A S

Если луч 1', отражённый от зеркала M1, и луч 2', отражённый от зеркала M2, падают в одну и ту же точку на экране с координатой $y$, разность фаз между ними может быть записана в виде:\[\delta_{1'2'}=\frac{2\pi}\lambda b\theta+\delta_y.\]

B4 Покажите в листах решений, что $$\delta_y=\delta_O-\cfrac{2\pi}{\lambda}\cdot 2\alpha y $$

Примечание: Далее во всех пунктах задачи можно пользоваться утверждениями пунктов B1-B4, даже если они не доказаны.

A S

B5 Таким образом, на экране возникнет интерференционная картина. Найдите расстояние $y_1$ до ближайшего к точке $O$ интерференционного максимума. Найдите также расстояние $\Delta y_m$ между двумя соседними интерференционными максимумами. Приведите численные ответы в случае $L_1=0.50~м$, $L_2=1.50~м$, $L_3=0.50~м$, $L_4=1.00~м$, $\alpha=10^{-4}$, $\theta=10^{-5}$, $\lambda=500~нм$.

A S

B6 Найдите, как интенсивность $I(y)$ на экране зависит от координаты $y$, если её максимальное значение равно $I_0$, подставив сюда численные значения из предыдущего пункта. Учтите влияние светоделителя на интенсивность прошедшего света.

A S

Часть C. Ну совсем произвольные лучи (1.0 балла)

Пусть теперь лучи 1'' и 2'' падают на интерферометр под углом $\theta_x\ll1$ к плоскости $yz$ и под углом $\theta_y\ll1$ к плоскости $xz$ (см. рис. 3).

C1 Выразите волновой вектор $\vec k$ падающих лучей через $\theta_x$, $\theta_y$, модуль волнового вектора $k=2\pi/\lambda$ и единичные орты координатных осей.

A S

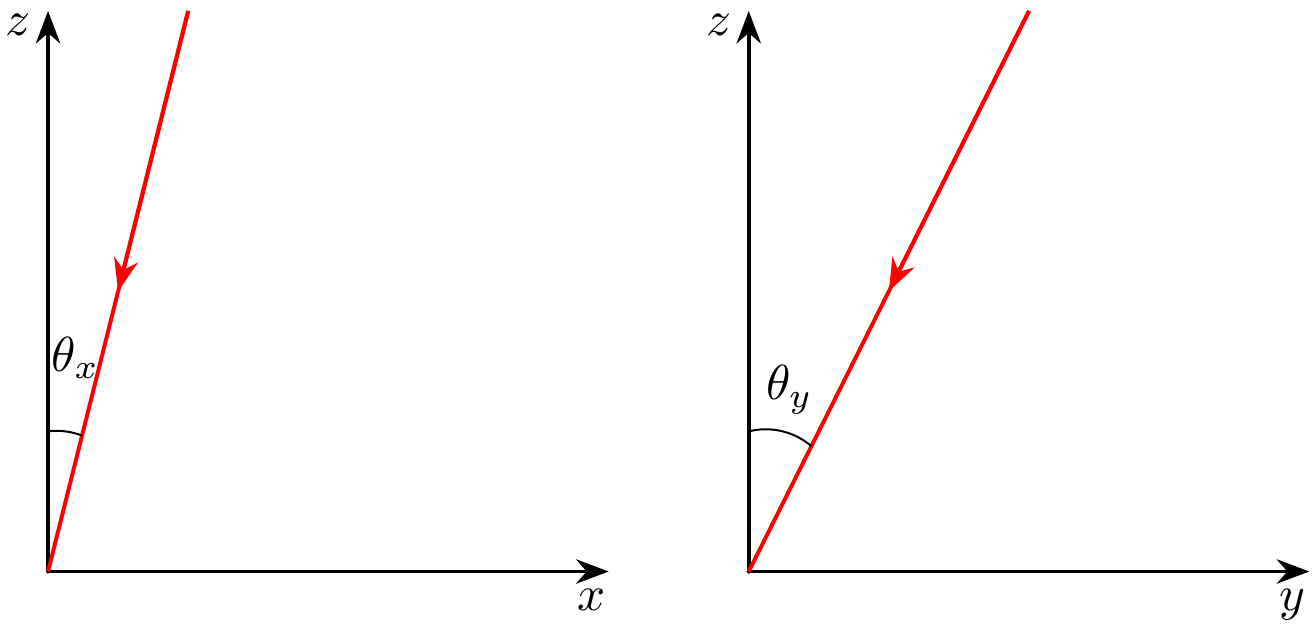
Итак, пусть луч ''1'', отражённый от зеркала M1, и луч ''2'', отражённый от зеркала M2, падают в одну и ту же точку на экране на оси $y$ на расстоянии $y$ от точки $O$.

C2 Выразите разность фаз между лучами 1'' и 2'' через $\lambda$, $L_1$, $L_2$, $L_3$, $L_4$, $\theta_x$, $\theta_y$, $\alpha$, $y$.

A S

Часть D. Измерение радиуса (2.7 балла)

Рассмотрим звезду с угловым радиусом $\theta_R$, который нам необходимо определить. Для простоты будем считать, что звезда излучает как однородный диск, т.е. интенсивность света, приходящего из телесного угла $\mathrm d\Omega=\mathrm d\theta_x\mathrm d\theta_y$, равна $\mathcal J\mathrm d\Omega$, где $\mathcal J$ — постоянная величина в любом направлении внутри диска звезды. 

Пусть интерферометр (а точнее, ось $z$) направлен точно в центр звезды. При $\alpha > 0$ на экране будет наблюдаться интерференционная картина. Обозначим минимальную и максимальную интенсивности на экране вдоль оси $y$ как $I_{y(min)}$ и $I_{y(max)}$ соответственно. Введём видность $V$ интерференционной картины как:\[V=\frac{I_{y(max)}-I_{y(min)}}{I_{y(max)}+I_{y(min)}}.\]

D1 Запишите $V$ в виде интеграла по одной переменной. Явно производить интегрирование при этом необязательно.

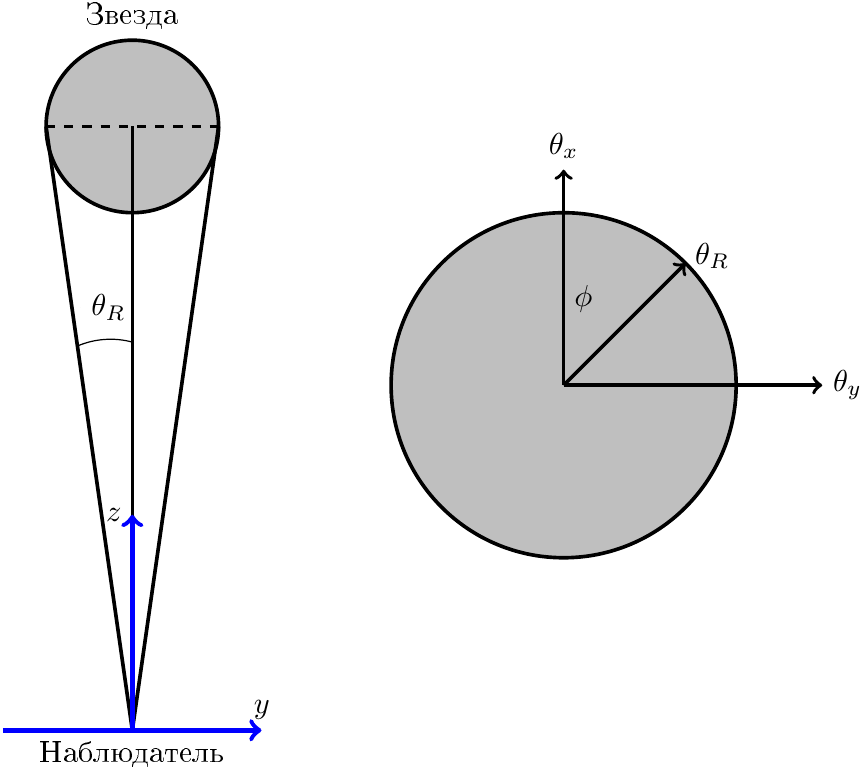
Подсказка: интеграл некоторой функции $f(\theta_y)$, зависящей только от $\theta_y$, по поверхности диска радиусом $\theta_R$ можно представить в виде:\[I=\int\limits_{-\theta_R}^{\theta_R}\mathrm d\theta_y\int\limits_{-\sqrt{\theta^2_R-\theta^2_y}}^{\sqrt{\theta^2_R-\theta^2_y}}\mathrm d\theta_x~f(\theta_y)=\int\limits_{-\theta_R}^{\theta_R}\mathrm d\theta_y\cdot 2\sqrt{\theta^2_R-\theta^2_y}f(\theta_y).\]

A S

Интерферометр используется для наблюдения Бетельгейзе. Если симметрично отдалять зеркала M1 и M2 от центра HM $\Big($так что $L_1^*=L_1+d/2$ и $L_2^*=L_2+d/2\Big)$, то видность $V$ обнулится при $d=0.97~м,3.12~м,\ldots$ (параметры системы те же, что и в B3). В данной части задачи $L_1$ и $L_2$ численно не заданы, а $\lambda=500~\text{нм}$.

D2 Найдите угловой радиус Бетельгейзе $\theta_R$. Найдите её радиус $R$, если расстояние до неё $h=6.079\cdot10^{15}~км$.

Подсказка: Первые два нуля интеграла\[F_n=\int_0^1\left(1-w^2\right)^n\cos(\eta w)~\mathrm dw\]как функции $\eta$ приведены в таблице ниже.

A S