Металлическое кольцо радиуса $R$ и толщины $2a\ll R$ равномерно заряжено зарядом $q$. Кольцо представляет собой тороид. В частях A, B, C и E следует пренебречь его толщиной. Кольцо лежит в плоскости $xy$, ось $z$ перпендикулярна плоскости кольца (см. Рис. 1). В частях A и B может пригодиться следующее разложение в ряд Тейлора:

Часть A. Потенциал на оси кольца (1 балл)

A1  ^0.30 Рассчитайте электростатический потенциал $\Phi(z)$ на оси кольца в точке A на расстоянии $z$ от его центра (см. рис. 1).

A2  ^0.40 Предполагая $z\ll R$, найдите потенциал $\Phi(z)$ в виде разложения в ряд до первого, зависящего от $z$, члена.

A3  ^0.20 Электрон (его масса $m$, заряд $-e$) расположили в точке A (см. рис. 1, $z\ll R$). Рассчитайте силу, действующую на электрон. Какой знак должен иметь заряд кольца $q$, чтобы возникли колебания? Смещение электрона не меняет распределение заряда по кольцу.

A4  ^0.10 Определите циклическую частоту $\omega$ этих гармонических колебаний.

Часть B. Потенциал в плоскости кольца (1.7 балла)

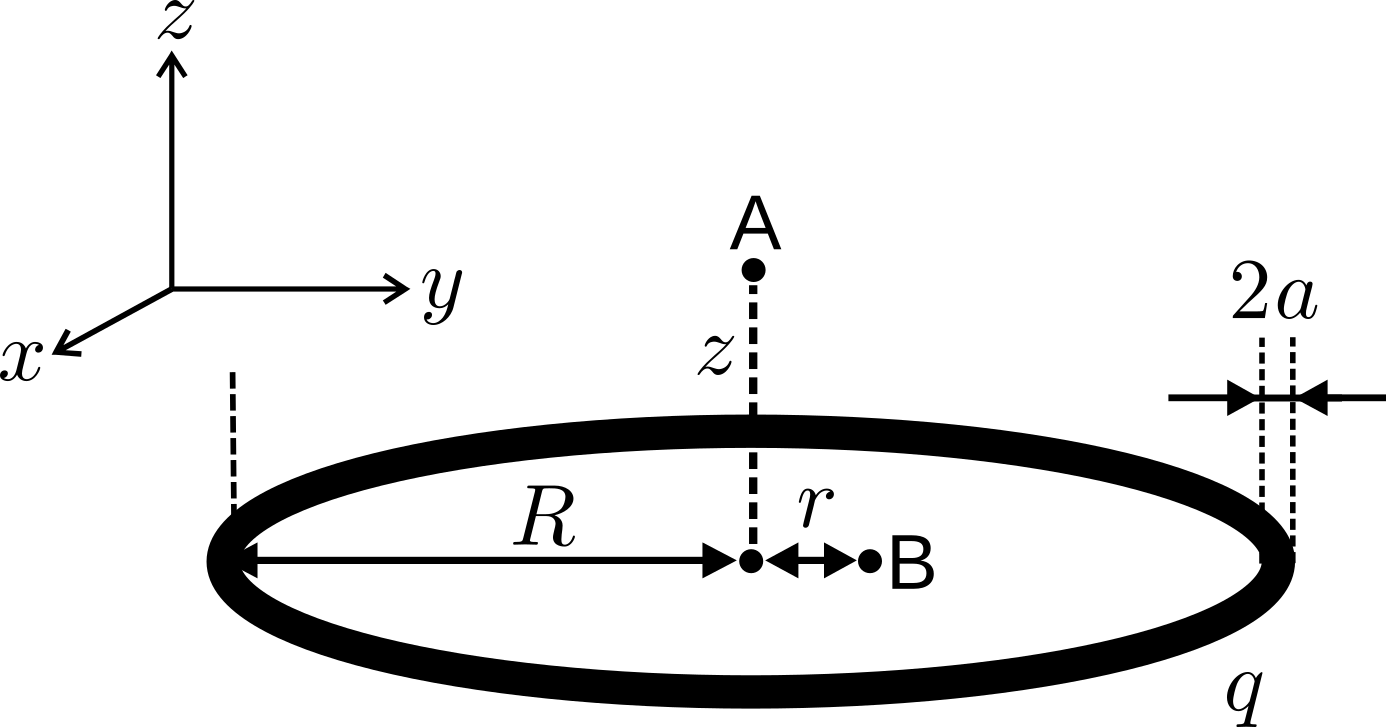
Теперь рассмотрим распределение потенциала $\Phi(r)$ в плоскости кольца ($z=0$) при $r\ll R$ (как в точке B на рис. 1). Разложение потенциала до первой ненулевой степени $r$ имеет вид $\Phi\approx q(\alpha+\beta r^2)$.

B1  ^1.50 Выразите $\beta$. Вы могли бы использовать разложение Тейлора, приведенное выше.

B2  ^0.20 Электрон расположили в точке B (см. рис. 1, $r\ll R$). Рассчитайте силу, действующую на электрон. Какой знак должен иметь заряд кольца $q$, чтобы возникли гармонические колебания? Смещение электрона не меняет распределение заряда по кольцу.

Часть C. Фокусное расстояние идеальной линзы: мгновенная зарядка (2.3 балла)

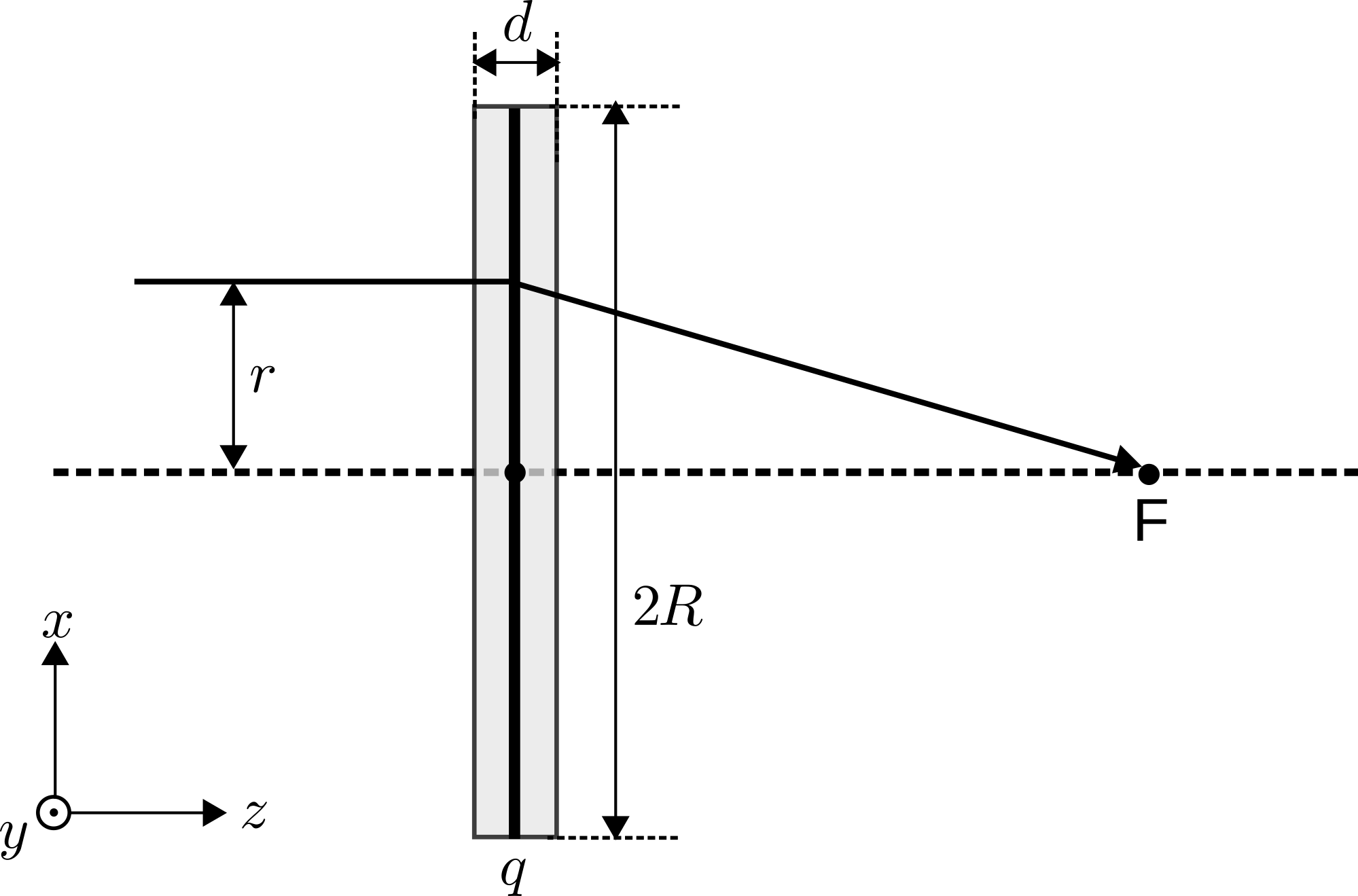
Экспериментатор Глюкас разрабатывает электростатическую линзу для фокусировки электронов. Он располагает кольцо перпендикулярно оси $z$ (см. рис. 2). Глюкас также конструирует источник, который генерирует пакеты (маленькие группы) нерелятивистских электронов. Кинетическая энергия электрона $E=mv^2/2$, ($v$ — скорость). При этом можно точно контролировать моменты времени, когда электроны вылетают из источника.

Заряд кольца нулевой почти всегда, и становится равным $q$, когда электроны находятся на расстоянии менее $d/2\:(d\ll R)$ от плоскости кольца (заштрихованная область на рис. 2 — «активная область»).

В этой части задачи предполагается, что Глюкас способен обеспечить мгновенную зарядку и мгновенную разрядку кольца, а электрическое поле мгновенно возникает в пространстве.

Магнитными полями, а также изменением $z$-компоненты скорости электронов следует пренебречь. Движущиеся электроны не влияют на распределение заряда по кольцу.

C1  ^1.30 Предположим, что пакет электронов изначально летит параллельно оси $z$ на расстоянии $r$ ($r\ll R$) от нее.

Определите фокусное расстояние $f$ линзы ($f\gg d$). Выразите ответ с использованием константы $\beta$ из пункта B.1 и других известных величин. Знак заряда $q$ таков, что линза работает как собирающая.

Предположим теперь, что точечный источник электронов расположен на оси $z$ на расстоянии $b>f$ от центра кольца. Из этой точки вылетают электроны под углами не более $\gamma \ll 1$ к оси $z$. Линза собирает их в некоторой точке на расстоянии $c$ от центра кольца.

C2  ^0.80 Найдите $c$. Выразите ответ с использованием константы $\beta$ из пункта B.1 и других известных величин.

C3  ^0.20 Выполняется ли формула тонкой линзы $\frac{1}{b}+\frac{1}{c}=\frac{1}{f}$ для линзы Глюка? Покажите это непосредственным расчетом величины $1/b + 1/c$.

Часть D. Емкость кольца (3 балла)

Рассмотренная модель линзы была идеализированной, и считалось, что кольцо заряжается мгновенно. В действительности это не так, потому что у кольца есть конечная емкость $C$.

Вам могут пригодиться следующие интегралы:

$$\int \frac{\mathrm{d} x}{\sin x}=-\ln \left|\frac{\cos x+1}{\sin x}\right|+ \mathrm{const}$$

и

$$\int \frac{\mathrm{d} x}{\sqrt{1+x^{2}}}=\ln \left|x+\sqrt{1+x^{2}}\right|+ \mathrm{const}$$

D1  ^2.00 Вычислите емкость $C$ кольца. Считайте, что ширина кольца $2a$, причем $a\ll R$.

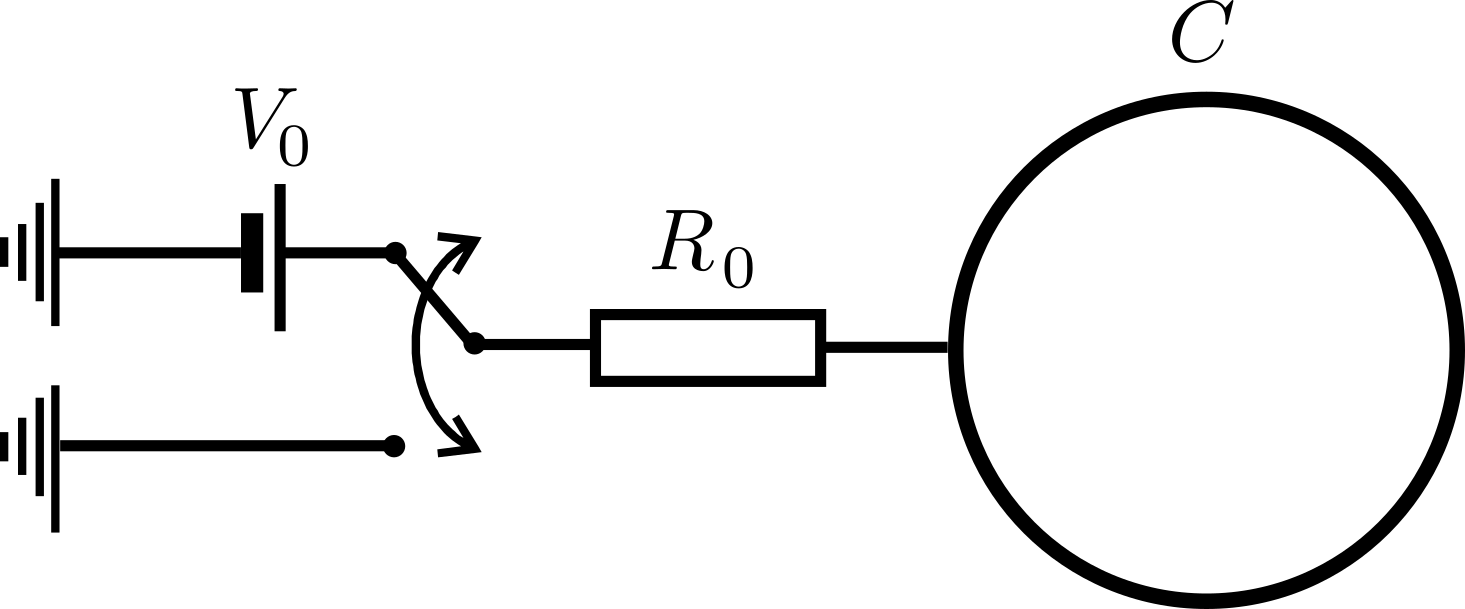
Рассмотрим следующую модель. Когда электроны достигают «активной области», кольцо подключают к источнику напряжения $V_0$ (рис. 3). Когда электроны покидают «активную область», кольцо заземляют. Сопротивление проводов равно $R_0$, а сопротивлением кольца можно пренебречь.

D2  ^1.00 Найдите, как зависит заряд кольца $q(t)$ от времени. Постройте схематический график этой зависимости. В момент времени $t=0$ электроны находятся в плоскости кольца.

В некоторый момент времени заряд кольца $q(t)$ достигает значения $q_0$, модуль которого максимален. Найдите это значение $q_0$. Емкость кольца $C$ (вам не нужно использовать значение из D.1).
Примечание: полярность подключения на рисунке 3 показана только в качестве примера. Подключение источника напряжения должно быть выбрано таким образом, чтобы линза работала как собирающая.

Часть Е. Фокусное расстояние реальной линзы: не мгновенная зарядка (2 балла)

В этой части задачи рассматривается более реалистичная модель линзы. Толщиной кольца $2a$ можно пренебречь. Перед тем как электроны достигают «активной области» они движутся параллельно оси $z$. Зарядку кольца больше нельзя считать мгновенной.

E1  ^1.70 Найдите фокусное расстояние $f$ линзы. Считайте, что $f/v\gg R_0C$, но $d/v$ и $R_0C$ одного порядка. Выразите ответ с использованием константы $\beta$ из части B и других известных величин.

E2  ^0.30 Можно заметить, что ответ для $f$ в предыдущем пункте похож на ответ, полученный в части C. Нужно только заменить значение заряда $q$ некоторым «эффективным» зарядом $q_\mathrm{eff}$. Выразите $q_\mathrm{eff}$ через заданные в задаче величины.