
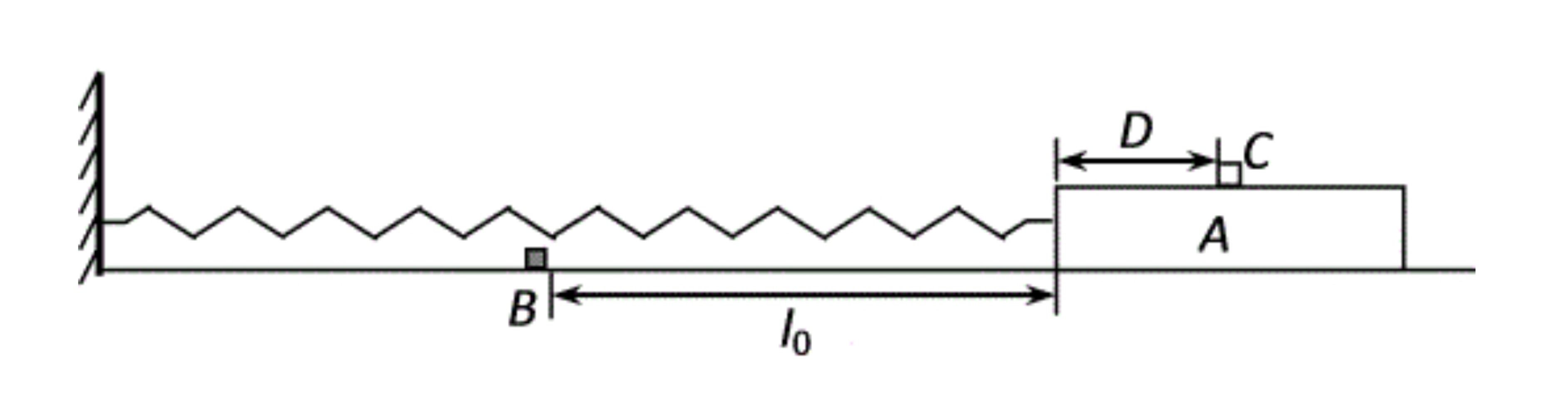
На рисунке (a) показана деревянная доска $A$, помещённая на гладкий горизонтальный стол, один из концов которой соединён со стеной при помощи идеальной пружины. На столе есть небольшая закреплённая преграда $B$. Когда доска контактирует с $B$, пружина находится в нерастянутом состоянии.
Доску $A$ оттягивают вправо на расстояние $l_0$, после чего помещают на неё пренебрежимо малых размеров деревянный брусок $C$ на расстоянии $D$ от её левого края, как показано на рисунке (b). Затем доску отпускают. Известны длина доски $L=0.7000~\text{м}$ и её масса $M=10.00~\text{кг}$, расстояние $l_0=1.000~\text{м}$, масса бруска $m=0.01000~\text{кг}$, жёсткость пружины $k=45.00~\frac{\text{Н}}{\text{м}}$ и коэффициенты трения покоя и скольжения между бруском и доской $\mu_0=0.4010$ и $\mu=0.4000$ соответственно. Столкновения между $A$ и $B$ абсолютно неупругие. Ускорение свободного падения равно $g=9.800~\frac{\text{м}}{\text{с}^2}$. Сопротивлением воздуха, массой пружины и влиянием бруска $C$ на движение доски пренебрегите.