
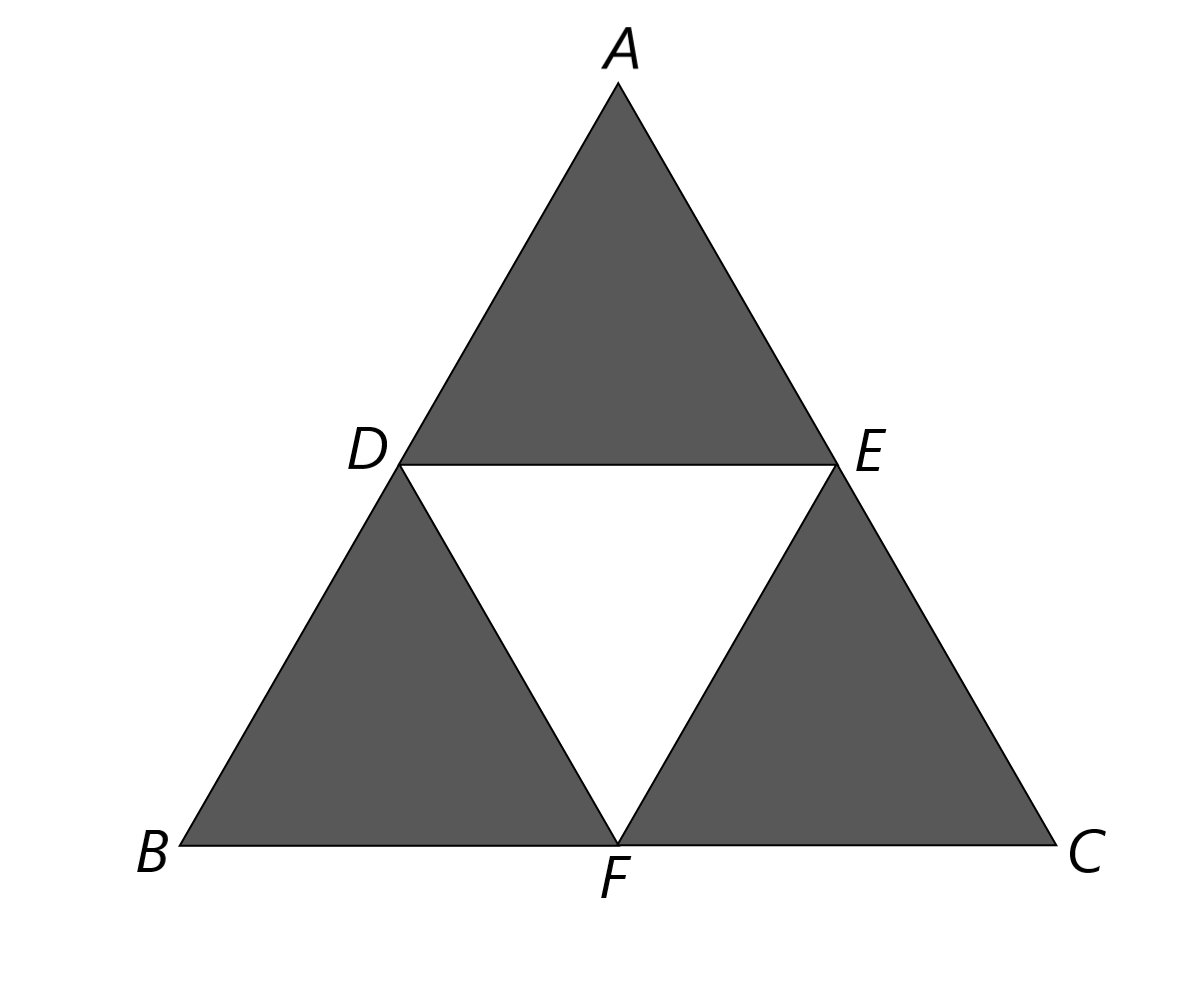
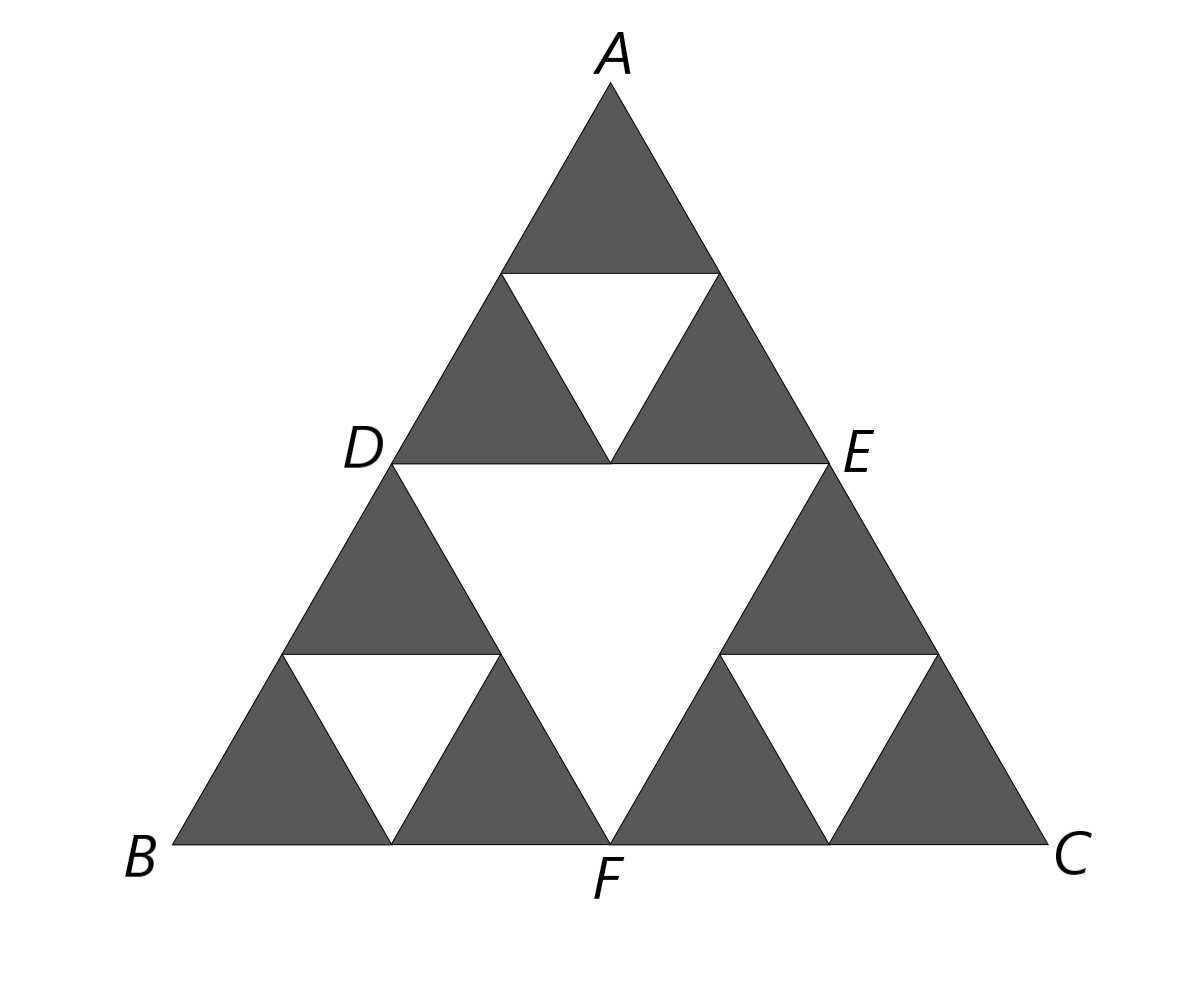
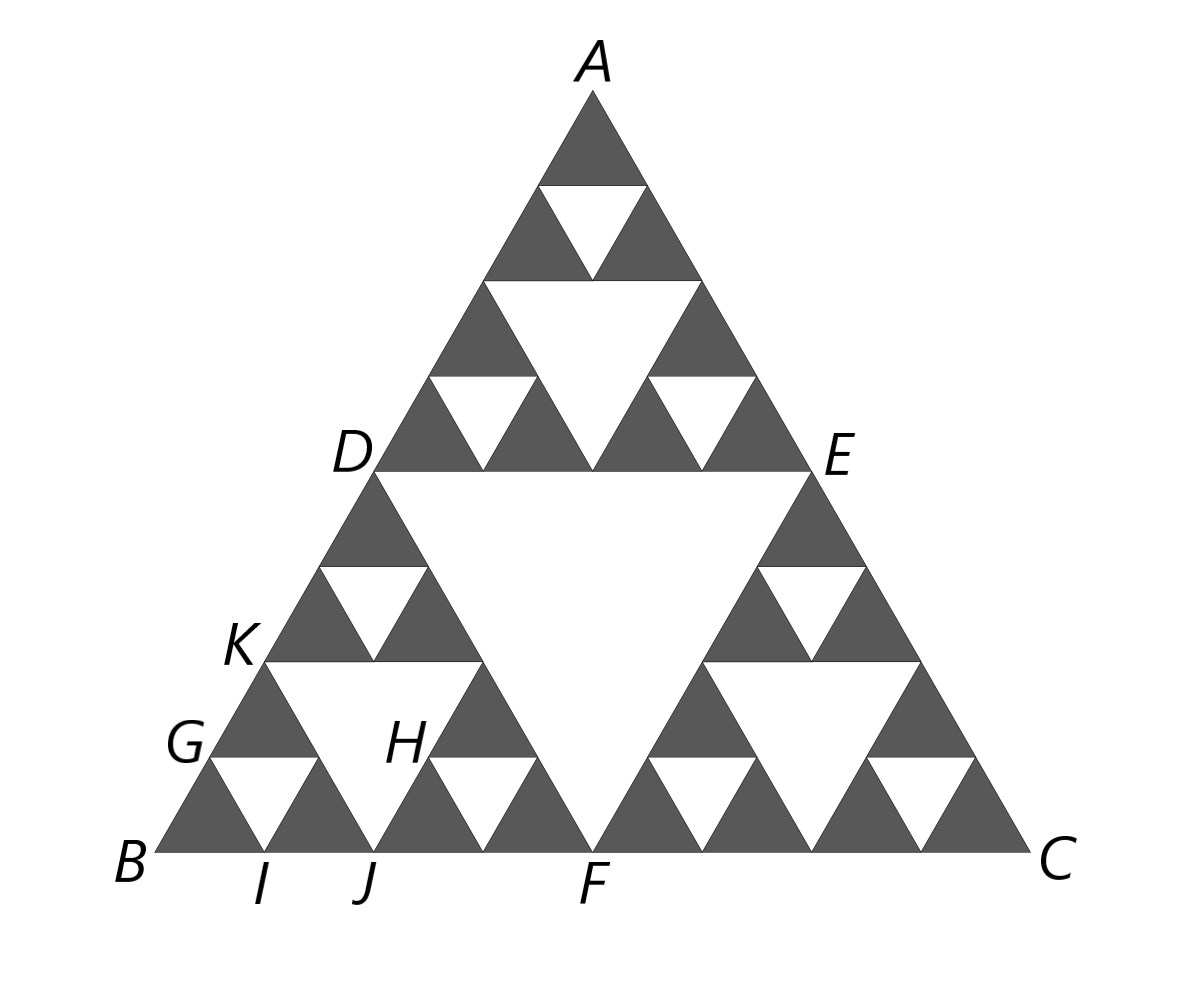
Польский математик Серпинский в 1916 году изучал свойства довольно примечательных геометрических фигур. Он разделил каждую сторону равностороннего треугольника $ABC$, показанного на рисунке (a), пополам и соединил получившиеся точки. Это разрезало $ABC$ на четыре одинаковых равносторонних треугольника. Затем средний треугольник был изъят, в результате чего получилась фигура, показанная на рисунке (b). Те же действия были произведены с оставшимися тремя треугольниками, и результатом второй итерации стала фигура на рисунке (c), а результатом третьей – фигура на рисунке (d). Полученные фигуры обладают важным свойством самоподобия. Если итеративный процесс продолжать бесконечно, то можно получить так называемый треугольник Серпинского.
Дальнейшие работы многих математиков по изучению подобных фигур привели с созданию так называемой фрактальной геометрии. В последние 30 лет физики активно применяют её методы в своих исследованиях и получают осмысленные результаты. В этой задаче будем исследовать эквивалентное сопротивление электрической цепи, состоящей из рёбер треугольника Серпинского. Сопротивление каждой стороны треугольника $ABC$ длиной $L_0$ равно $r$, сопротивление половины стороны, полученной в результате разделения, равно соответственно $\frac{r}{2}$, и т.д.
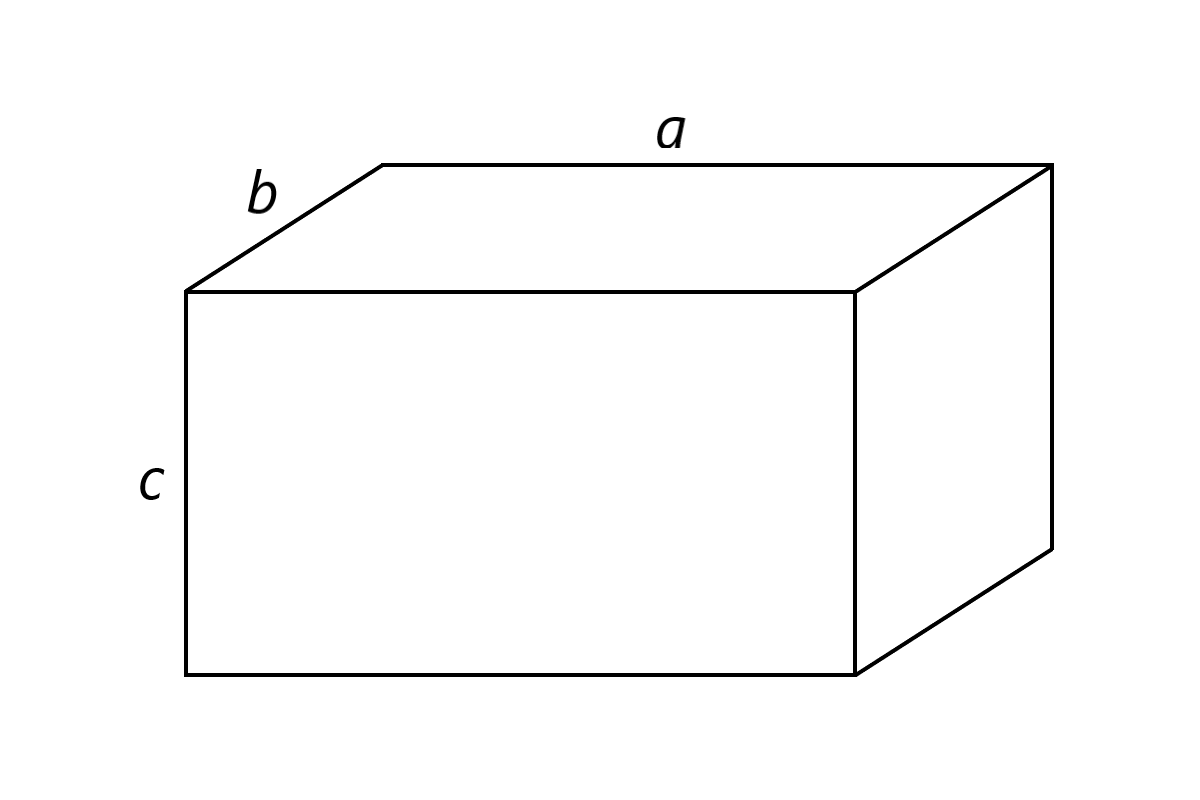
Как видим, в ходе итеративного процесса получения треугольника Серпинского сторона самых маленьких составляющих его треугольников уменьшается, и эквивалентное сопротивление треугольника может быть выражено через эту длину. Для описания свойств проводящих систем с этой точки зрения полезно будет ввести понятие их эффективной размерности $s$. Проиллюстрируем его следующим образом. Рассмотрим однородный проводящий прямоугольный параллелепипед с длиной, шириной и высотой $a$, $b$ и $c$ соответственно, как показано на рисунке, ток по которому протекает параллельно $a$. Его сопротивление будет равно$$R=\rho \frac{a}{bc},$$где $\rho$ – удельное сопротивление материала. Если длины сторон $b$ и $c$ зафиксировать, а длину $a=L$ менять, то сопротивление такого проводника будет равно$$R_{(1)}(L)=\rho\frac{L}{bc}\propto L^1,$$и его эффективная размерность будет равна $s=1$. Если же теперь зафиксировать длину стороны $c$ и менять длины $a=b=L$, то сопротивление будет равно$$R_{(0)}(L)=\rho\frac{1}{c}\propto L^0,$$ его эффективная размерность будет равна $s=0$. Аналогично, если $a=b=c=L$, то получим$$R_{(-1)}(L)=\rho\frac{1}{L}\propto L^{-1}$$и эффективную размерность $s=-1$. Таким образом, в общем случае эффективной размерность проводника равна $s$, если его сопротивление можно представить в виде$$R_{(s)}(L)=kL^s,$$где $k$ — коэффициент пропорциональности, а $L$ — характерная длина.
В треугольнике Серпинского длина стороны изначального треугольника равна $L_0$, а характерной длиной $L$ является длина стороны наименьшего треугольника.