Когда близорукий человек не носит очки, все объекты, которые он может чётко видеть, находятся на расстоянии не более $a=20~\text{см}$ от его глаз. Однако, если поместить перед глазами такого человека лист с маленьким отверстием, он сможет различать без очков и отдалённые объекты, глядя через это отверстие.

1 Вычислите в рамках геометрической оптики диаметр светового пятна $D'$, образующегося на сетчатке глаза близорукого человека, когда он смотрит на отверстие диаметра $D$.

$\textit{Примечание:}$ человеческий глаз представляет собой оптическую систему со сложной структурой. В рамках данной задачи её можно упростить, представив глаз как систему из тонкой линзой с изменяемым фокусным расстоянием $f$ и сетчатки, на которой формируется изображение. Можно также считать, что размеры этой линзы определяются размерами зрачка, среда по обе стороны её представляет собой воздух, а расстояние между линзой и сетчаткой равно $b$.

2 Учитывая, что свет испытывает дифракцию на маленьком отверстии, найдите его оптимальный диаметр $D_0$. Считайте, что видимый свет в среднем имеет длину волны $\lambda=600~\text{нм}$.

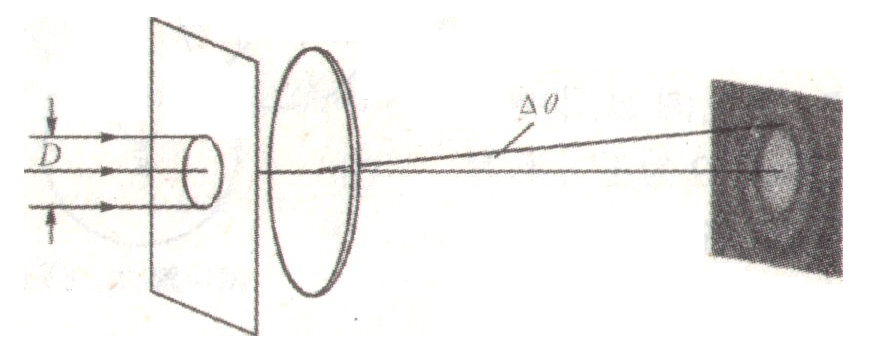
$\textit{Примечание:}$ Поясним влияние наличия маленького круглого отверстия на создаваемое линзой изображение. В рамках геометрической оптики лучи света, испущенные удалённым источником и потому параллельные оптической оси соберутся строго в фокусе линзы, создавая изображение. Однако, если поместить перед линзой маленькое круглое отверстие диаметра $D$, произойдёт дифракция света, поэтому в фокальной плоскости появится дифракционная картина, показанная на рисунке (a).

В центре картины располагается яркое круглое пятно, а за его пределами — множество тёмных и светлых концентрических колец с постепенно убывающей яркостью. В силу того, что яркость этих колец много меньше, чем у центрального пятна, их наличием можно пренебречь. Тогда радиус $\Delta\theta$ центрального пятна будет связан с $D$ как\[\Delta\theta=1.22\frac{\lambda}{D},\]где $\lambda$ — длина волны используемого света. «Изображением» точечного источника при наличии маленького круглого отверстия является центральное пятно, как показано на рисунке (b). Несложно видеть, что с ростом $D$ это пятно уменьшается в размерах, становясь в пределе точечным, а изображение при этом становится чётче. С другой стороны, при уменьшении $D$ размер дифракционного пятна увеличивается, и изображение ухудшается. Если экран, на котором формируется изображение, находится не строго в фокусе, а в некоторой его окрестности, на экране можно будет наблюдать ту же дифракционную картину, и угловой радиус $\Delta\theta$ центрального пятна может быть приближённо вычислен по той же формуле.