Какую работу нужно совершить, чтобы вытащить кольцо из щели и перенести его на большое расстояние от бруска? Гистерезисом материала пренебречь.
Пусть $\Phi$ - полный поток магнитного поля (как самого витка, так и бруска), пронизывающего виток.
Покажем, что поскольку гистерезисом в бруске можно пренебречь, магнитная энергия системы $W$ при силе тока $I_\text{в}$ в витке равна:
$$W=\cfrac{\Phi I_\text{в}}{2}{.}
$$
Рассмотрим виток с нулевой силой тока в нём. Тогда, работа источника, медленно увеличившего силу тока в витке до $I_\text{в}$ будет равна магнитной энергии системы.
При увеличении силы тока, в витке возникает ЭДС индукции, компенсируемая источником. Отсюда:
$$\mathcal{E}_\text{ист}=\cfrac{d\Phi}{dt}{.}
$$
Тогда для мощности и работы источника соответственно получим:
$$P_\text{ист}=I_\text{в}\cfrac{d\Phi}{dt}\Rightarrow{A_\text{ист}=\int\limits_0^{\Phi}I_\text{в}d\Phi}{.}
$$
Поскольку брусок является однородным и линейным ферромагнетиком, во всех точках создаваемое им магнитное поле прямо пропорционально силе тока тока $I_\text{в}$.
Значит, магнитный поток $\Phi$ также прямо пропорционален $I_\text{в}$. Отсюда имеем:
$$A_\text{ист}=\cfrac{\Phi I_\text{в}}{2}=W{.}
$$
Магнитные энергии системы $W_1$ и $W_2$ внутри и вдали от бруска равны соответственно:
$$W_1=\cfrac{\Phi I}{2}\qquad W_2=\cfrac{\Phi^2}{2L}{,}
$$
откуда работа по перемещению витка равняется:
$$A=W_2-W_1=\cfrac{\Phi^2}{2L}-\cfrac{\Phi I}{2}{.}
$$
Задача свелась к нахождению магнитного потока $\Phi$.
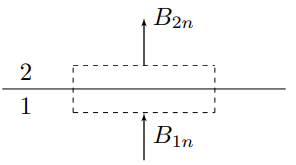
Пусть $\vec{B}_1$ и $\vec{B}_2$ - индукции магнитного поля внутри и вне щели соответственно на границе раздела.
Воспользуемся теоремой Гаусса для индукции магнитного поля в пределе бесконечно тонкого цилиндра, ось которого перпендикулярна границе раздела:
$$\oint_S\vec{B}d\vec{S}=\left(B_{2n}-B_{1n}\right)dS=0\Rightarrow{B_{2n}=B_{1n}}{.}
$$
Таким образом, нормальная компонента индукции магнитного поля не изменяется при переходе через границу раздела.
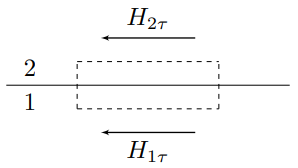
Пусть $\vec{H}_1$ и $\vec{H}_2$ - напряжённости магнитного поля внутри и вне щели соответственно на границе раздела.
Воспользуемся теоремой о циркуляции для вектора напряжённости магнитного поля в пределе бесконечно узкого прямоугольного контура, пара из сторон которого параллельна границе раздела:
$$\oint_L\vec{H}d\vec{l}=I_\text{ст}=0\Rightarrow{H_{1\tau}=H_{2\tau}}{.}
$$
Таким образом, тангенциальная компонента напряжённости магнитного поля не изменяется при переходе через границу раздела.
Также для линейных и однородных магнетиков с проницаемостью $\mu$ верно:
$$\vec{B}=\mu_0\mu\vec{H}{.}
$$
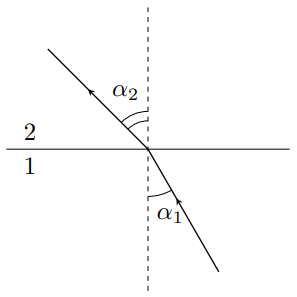
Пусть $\alpha_1$ и $\alpha_2$ - углы падения и преломления соответственно индукции магнитного поля на границе раздела. Тогда:
$$\tan\alpha_1=\cfrac{B_{1\tau}}{B_{1n}}\quad\tan\alpha_2=\cfrac{B_{2\tau}}{B_{2n}}{.}
$$
Поскольку $H_{1\tau}=H_{2\tau}$, имеем:
$$B_{1\tau}=\cfrac{B_{2\tau}}{\mu}{,}
$$
откуда:
$$\tan\alpha_1=\cfrac{\tan\alpha_2}{\mu}{.}
$$
Поскольку толщина зазора мала - магнитное поле, создаваемое витком на границе раздела, направлено перпендикулярно ей, и, поскольку по условию $\mu\gg{1}$ - $\alpha_1\to{0}$.
Тогда в области зазора магнитное поле направлено перпендикулярно плоскости витка.
Применяя теорему о циркуляции к прямоугольному контуру, целиком расположенному в зазоре, получим, что магнитное поле в области зазора практически однородно.
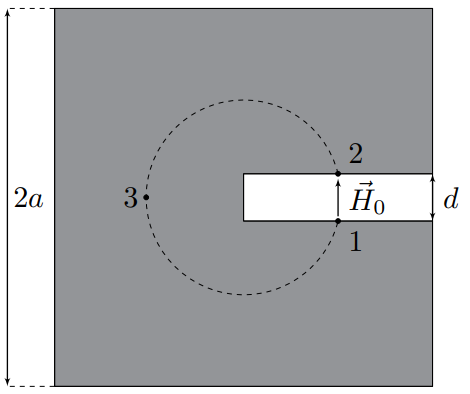
Далее рассмотрим циркуляцию вектора $\vec{H}$ по такому контуру $1231$, проходящему внутри куба, что одна из его частей является отрезком длиной $d$, перпендикулярным плоскости витка. При этом ток в витке пересекает контур $1231$.
Имеем:
$$I=\oint_L\vec{H}d\vec{l}=\int_{12}\vec{H}d\vec{l}+\int_{231}\vec{H}d\vec{l}\approx{H_0d+\overline{H}a}{,}
$$
где $\overline{H}$ - среднее по длине траектории значение компоненты $H_l$, направленной по касательной к кривой, по которой производится интегрирование.
Поскольку $\alpha_1\to{0}$ - тангенциальная компонента $H_\tau\to{0}$, откуда следует, что внутри бруска величина $\overline{H}$ имеет следующий порядок:
$$\overline{H}\cong{\cfrac{H_0}{\mu}}{.}
$$
Поскольку по условию $\mu d\gg{a}$, соотношение между слагаемыми, входящими в циркуляцию вектора $\vec{H}$ по контуру $1231$ следующее:
$$\overline{H}a\cong{\cfrac{H_0a}{\mu}}\ll{H_0d}{.}
$$
Отсюда находим:
$$H_0\approx{\cfrac{I}{d}}{.}
$$
Тогда, поскольку магнитное поле в области зазора можно считать однородным, имеем:
$$\Phi=\cfrac{\pi{a}^2B_0}{4}=\cfrac{\mu_0\pi{a}^2I}{4d}{,}
$$
откуда окончательно имеем:
Ответ:
$A=\cfrac{\mu_0\pi I^2a^2}{8d}\left(\cfrac{\mu_0\pi a^2}{4dL}-1\right)$