Обозначим искомую ёмкость между вершинами $B$ и $E$ за $C_{BE}$.
Рассмотрим додекаэдр целиком (т.е с конденсаторами $AB$ и $AD$).
Пусть при подключении источника к вершинам $B$ и $E$ ёмкость додекаэдра равна $C_0$. Поскольку конденсатор $AD$ в силу симметрии окажется не заряженным, эквивалентная схема додекаэдра представляет собой параллельно соединённые конденсаторы ёмкостями $\cfrac{C}{2}$ и $C_{BE}$. Отсюда:
$$C_{BE}=C_0-\cfrac{C}{2}
$$

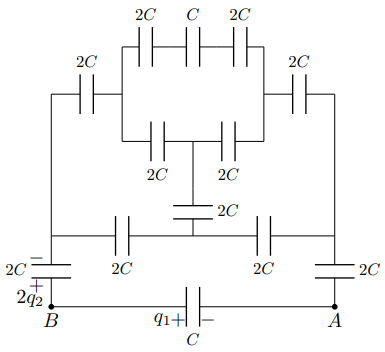
Пропустим пробный заряд $q$ между узлами $B$ и $A$, а затем между узлами $A$ и $E$, что в результате даст заряд $q$, пропущенный между узлами $B$ и $E$.
Пусть при подключении к узлам $BA$ заряды конденсаторов $BA$ и $EA$ оказались равны $q_1$ и $q_2$ соответственно, а обкладки, соединённые с узлом $A$, заряжены отрицательно. Тогда при подключении к узлам $A$ и $E$ заряды конденсаторов $BA$ и $EA$ равны $q_2$ и $q_1$ соответственно, а обкладки, соединённые с узлом $A$, заряжены положительно.
При наложении подключений имеем:
$$q_{BA}=q_{EA}=q_1-q_2
$$
Тогда для ёмкости $C_0$ имеем:
$$C_0=\cfrac{q}{U_{BE}}=\cfrac{q}{\cfrac{q_{BA}}{C}+\cfrac{q_{EA}}{C}}=\cfrac{C}{2\left(\cfrac{q_1}{q}-\cfrac{q_2}{q}\right)}
$$

С учётом симметрии, эквивалентная схема при подключении к $BA$, а также введённые заряды $q_1$ и $q_2$ представлены на рисунке. Здесь мы убрали из рассмотрения два конденсатора, перпендикулярные плоскости симметрии системы, а затем полученную схему сложили пополам. Двое конденсаторов не имеют пары и их ёмкость в эквивалентной схеме остаётся равной $C$, а остальные конденсаторы имеют пару, поэтому при параллельном соединении эквивалентная ёмкость каждого из них равна $2C$.
После упрощения, схема представляет собой два параллельных конденсатора с ёмкостями $C$ и $11C/19$ с зарядами $q_1$ и $2q_2$ соответственно.
Имеем:
$$
\begin{cases}
q=q_1+2q_2\\
\cfrac{2q_2}{q_1}=\cfrac{11}{19}
\end{cases}
\Rightarrow{\cfrac{q_1}{q}=\cfrac{19}{30}\quad\cfrac{q_2}{q}=\cfrac{11}{60}}
$$
Подставляя найденные отношения, найдём:
$$C_0=\cfrac{C}{2\left(\cfrac{19}{30}-\cfrac{11}{60}\right)}=\cfrac{10C}{9}
$$
Окончательно для $C_{BE}$ получим: