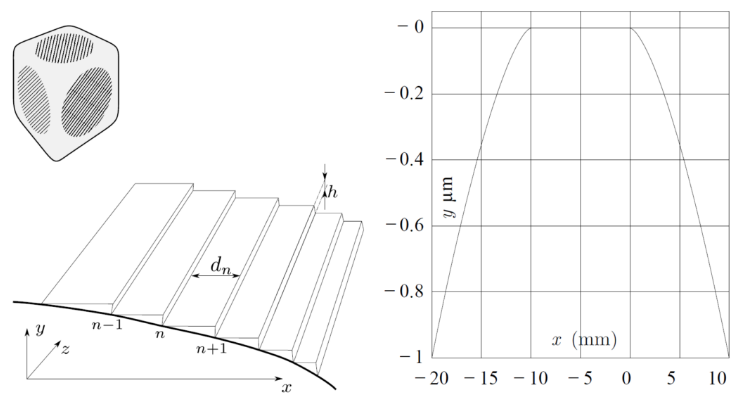
Равновесная форма тел в отсутствии силы тяжести определяется минимумом их поверхностной энергии. При низких температурах равновесные формы кристаллов могут иметь плоские грани. Части поверхности кристалла, которые составляют малый угол $\phi$ с гранью, представляют собой лесенки из редких ступеней на данной грани (см. рисунок ниже). Высота такой ступеньки равна периоду кристаллической решетки $h$.
Сечение $y(x)$ равновесной формы некоторого кристалла и соответствующая лесенка показаны на рисунке слева. $n$ обозначает номер ступеньки, начиная с $x=0$. Сечение формы этого кристалла показано на графике, при $x > 0$ зависимость можно аппроксимировать как $y(x)=-(x/\lambda)^{3/2}h, \lambda=45~\text{мкм}, h=0.3~\text{нм}$.
Этот кристалл изучался а задаче Европейской олимпиады (E18-T3), где было показано, что расстояние $d_n$ между соседними ступеньками для $n\gg 1$ выражается как $d_n=30~\text{мкм}~n^{1/3}$, а энергия взаимодействия $E$ двух ступенек зависит от расстояния между ними $E(d)=\mu d^{-2}$. Здесь считается, что только соседние ступени взаимодействуют, а $E(d)$ — это энергия взаимодействия, приходящаяся на единицу длины ступени.