1  ^10,00 Предположим, что свет падает на границу раздела двух материалов с разными показателями преломления. Для всех возможных случаев на рисунках выше найдите оптический путь двух соседних лучей и покажите, что обобщённый закон Снеллиуса выполняется.

Достаточно воспользоваться принципом Гюйгенса для волновых фронтов, как показано на рисунке ниже.

2  ^13,00 Сферическая поверхность радиуса $R$ с центром в точке $C$ делит трёхмерное пространство на внутреннюю и внешнюю область с $n_2<0$ и $n_1>0$. Рассмотрим произвольную оптическую ось, проходящую через $C$, и примем точку $O$ на пересечении оси со сферой за начало координат. Луч $x$ падает на сферу в точке $M$ и преломляется, переходя в луч $y$, как показано на рисунке. Расстояния от начала координат до объекта и изображения равны $s_1$ и $s_2$ соответственно. В параксиальном приближении запишите формулу такой линзы (связывающую $s_1$, $s_2$ и параметры системы) и найдите увеличение линзы. В ответах обязательно указывайте корректные знаки полученных величин.

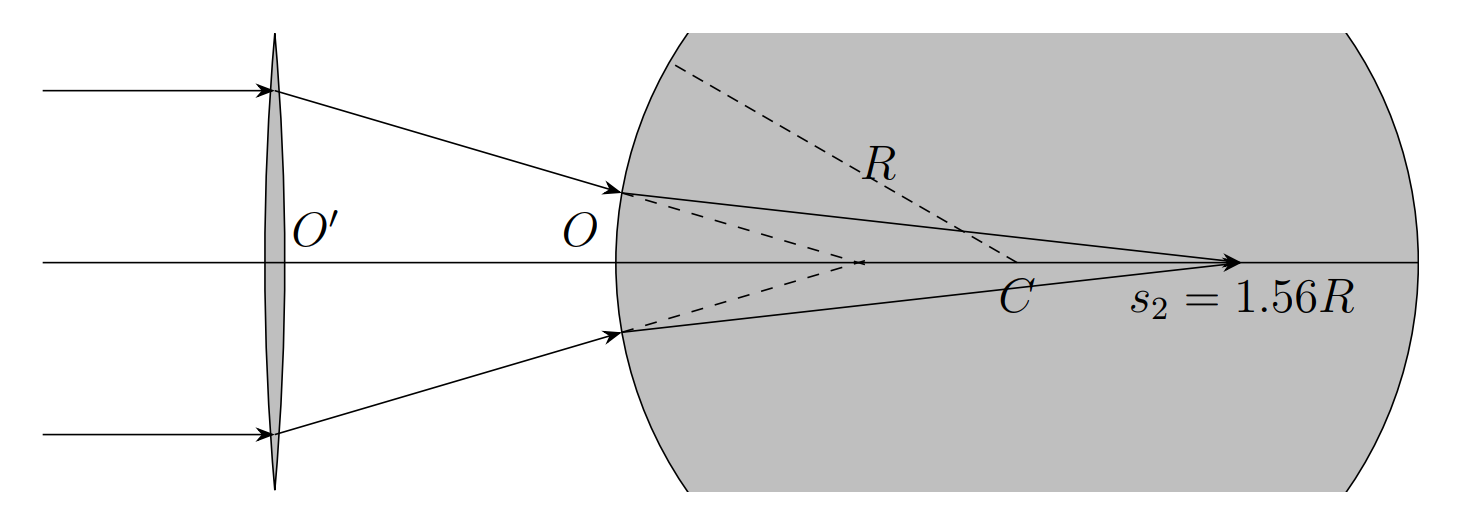
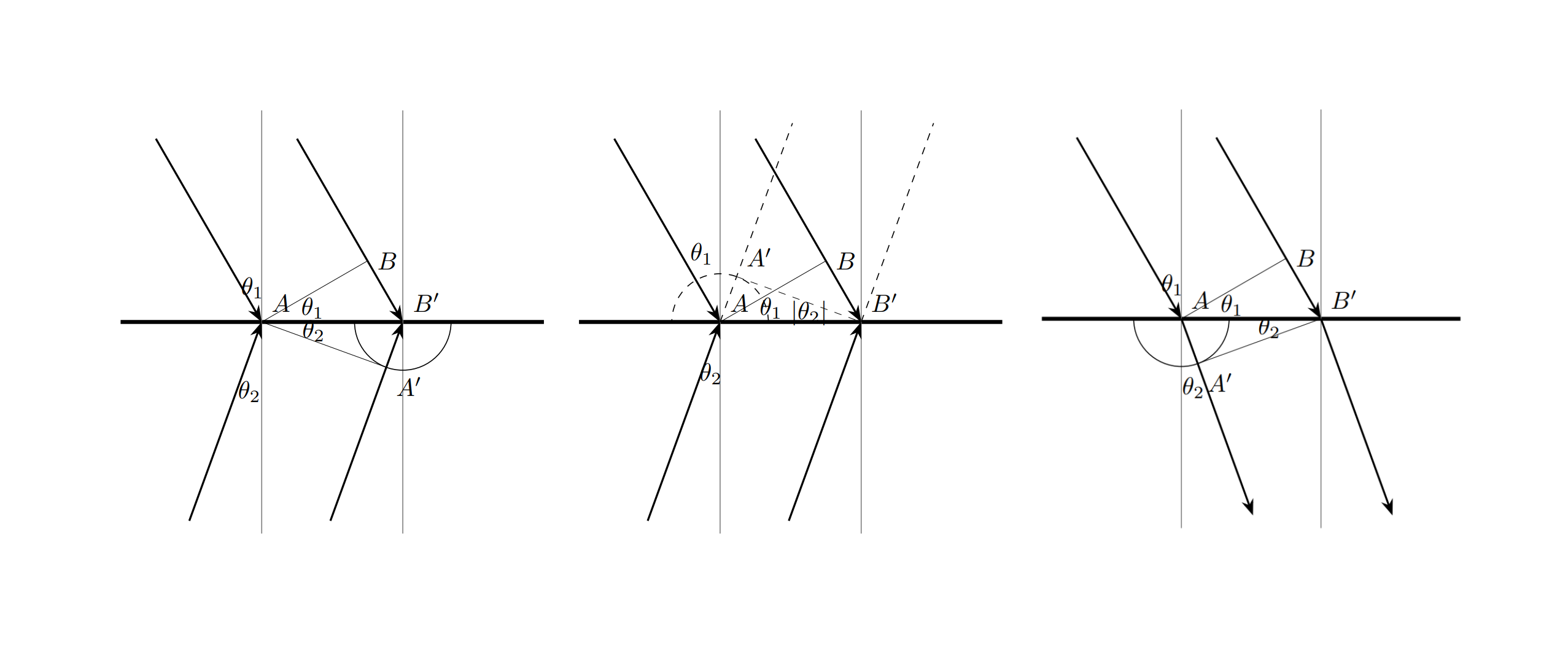
3  ^12,00 Предположим, что первая среда — это воздух, и $n_1 \approx 1$, $n_2$ же может принимать как положительные, так и отрицательные значения. Поместим собирающую линзу с фокусным расстоянием $f = 1.5R$ перед сферой так, чтобы оптическая ось линзы проходила через $C$ и один из фокусов находился внутри сферы. Расстояние между $O$ и центром линзы $O'$ равно $d$. Параллельный оптической оси пучок света падает на линзу. Для каждого случая из таблицы ниже найдите расстояние от точки $O$ до точки, в которой свет сфокусируется. Изобразите путь лучей для случая 4.