Часть A. Отверстие

На круглое отверстие радиуса $R_0$ в непрозрачной плоскости падает плоская монохроматическая волна с длиной волны $\lambda$ интенсивности $I_0$ параллельно оси отверстия. За плоскостью находится экран на расстоянии $L$. Считайте, что $\frac{ \sqrt{\lambda L}}{R_0} \gtrsim 1$.

A1 Оцените радиус пятна $R$ на экране.

S

A2 Оцените интенсивность $I$ в центре пятна.

S

A3 Оцените минимальный достижимый радиус пятна $R_{\text{min}}$ при варьировании радиуса отверстия.

S

Часть B. Обычная линза

На линзу диаметра $D$ и фокусного расстояния $F$ падает плоская монохроматическая волна с длиной волны $\lambda$ интенсивности $I_0$ параллельно оси линзы.

B1 Оцените диаметр $D_F$ пятна в фокусе линзы.

S

B2 Оцените интенсивность $I_F$ в фокусе линзы из энергетических соображений.

S

B3 Теперь посчитайте ответ для интенсивности $I_F$ в фокусе линзы точно. Сравните с предыдущим пунктом.

S

Часть С. Уже не очень линза

На идеальное параболическое зеркало параметра параболы $p$ и диаметра $D$ падает плоская монохроматическая волна с длиной волны $\lambda$ и интенсивностью $I_0$ параллельно оси зеркала. Данная

С1 Найдите фокусное $F$ расстояние зеркала.

S

С2 Оцените интенсивность $I$ в фокусе зекрала.

S

С3 Во сколько раз изменится это значение при уменьшении длины волны в два раза?

S

Часть D. Почти как линза

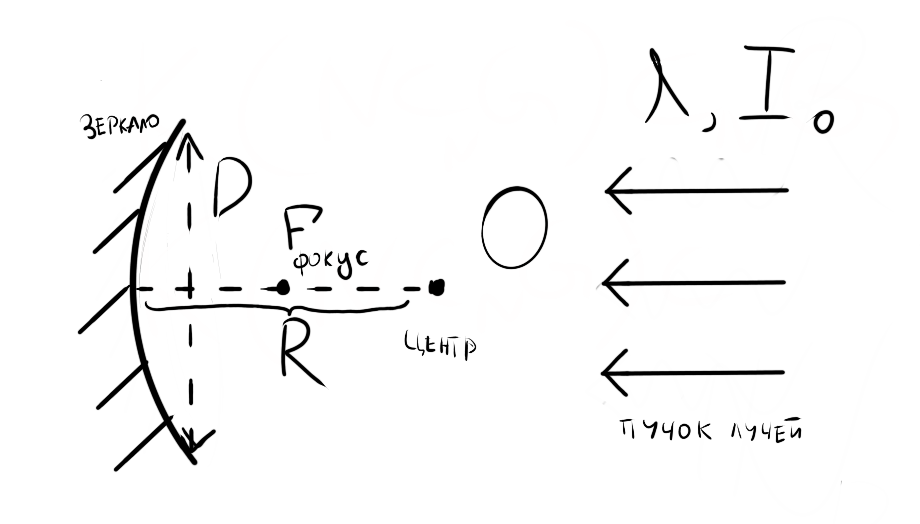
На идеальное сферическое зеркало радиусом $R = 1 м$ и диаметром $D$ посветили пучком лучей с длиной волны $\lambda = 800$ нм и с интенсивностью $I_0$ параллельно оси зеркала.

D1 Найдите фокусное расстояние $F$ зеркала.

S

D2 Оцените размер пятна $d$ в фокальной плоскости зеркала, для двух диаметров зеркала: $D_1 = 1~см$, $D_2 = 15~см$.

S

D3 Для этих двух диаметров зеркал ($D_1 = 1~см$, $D_2 = 15~см$) оцените интенсивность в фокусе.

S

D4 Как найденные в прошлом пункте интенсивности в фокусе зависят от длины волны $\lambda$?

S

Часть E. Вообще не линза

На дифракционную решетку с периодом $d$ и шириной щели $a$ падает нормально плоская волна. Длина волны $\lambda = d/100$, интенсивность плоской волны $I_S$.

Далее под интенсивностью максимума следует понимать интенсивность плоской волны, распространяющейся в направлении максимума с номером $h$.

E1 Определите интенсивность нулевого максимума $I_0$. Выразите ответ в общем виде через $d$ и $a$. Укажите ответ для $d=3a$.

S

E2 Определите интенсивность $I_h$ максимума с номером $h$. Выразите ответ в общем виде через $d$ и $a$. Укажите ответ для $d=3a$.

S

E3 Какая доля энергии $\beta$ попадает во все максимумы на экране, кроме нулевого $(h≠0)$? Вычислите ответ для $d=3a$.

S

E4 Какая доля энергии $\gamma$ поглощается не пропускающей частью дифракционной решеткой? Вычислите ответ для $d=3a$.

S