
Вначале отметим, что огибающая траекторий шариков, брошенных из начала координат с одинаковой скоростью $v$ под разными углами является параболой. Фокусом параболы является точка бросания.
Это можно показать следующим образом. Траектория шарика выражается параметрически как $x=vt\cos\alpha,y=vt\sin\alpha -\cfrac{1}{2}gt^2$. Исключая $t$, получаем
$$y=x\operatorname{tg}\alpha -\cfrac{g}{2v^2}x^2(1+\operatorname{tg}^2\alpha).$$
Мы можем считать это уравнение уравнением для нахождения угла $\alpha$, чтобы была достигнута точка $(x,y)$:
$$gx^2\operatorname{tg}^2\alpha -2v^2x\operatorname{tg}\alpha +2v^2y+gx^2=0.$$
Точки на огибающей разделяют точки, для которых решение данного уравнения существует и точки, для которых решение не существует. Поэтому для точек на огибающей дискриминант уравнения равен нулю:
$$v^4x^2=gx^2\left(2v^2y+gx^2\right)\implies y=\cfrac{v^2}{2g}-\cfrac{gx^2}{2v^2}.$$
Мы получили параболу. Положение ее фокуса может быть получено из данной формулы. С другой стороны, положение фокуса может быть получено из того, что световые лучи, параллельные оси параболы, сходятся после отражения от параболы в ее фокусе. Разумеется, точка касания огибающей и траектории при угле вылета $\alpha=45^\circ$ должна находиться при $y=0$. При этом угле вылета достигается максимальная дальность. Следовательно, огибающая и ось x встречаются при $y=0$, так что вертикальный луч, падающий на образующую при $y=0$, отражается от образующей горизонтально. Фокус должен находиться на отраженном луче, то есть при $y=0$.
Параболическая траектория каждой частицы воды должна касаться огибающей.Так как углы вылета воды из шланга не могут быть меньше $45^\circ$, точка касания должна находиться при $y\ge 0$. Это следует из того, что частица воды, выпущенная под $45^\circ$, попадет на образующую при $y=0$, а увеличение угла вылета увеличит высоту точки касания.
Есть много способов доказать последнее более точно. Например, можно использовать тот факт (доказанный ниже), что скорость вылета воды из шланга и касательная к огибающей в точке $A$, где траектория и огибающая совпадают, взаимно перпендикулярны: $\alpha+\beta=90^\circ$ ($\beta$ — угол между касательной и горизонтом). Отсюда увеличение $\alpha$ ведет к уменьшению $\beta$ и, следовательно, к подъему $A$. Для доказательства того, что $\alpha+\beta= 90^\circ$ предположим, что вертикально направленный луч отражается от траектории в точке $A$. Он пройдет через фокус траектории. Если мы его продолжим дальше фокуса и отразим его второй раз от той же траектории, он будет направлен вертикально вниз. Траектория и образующая являются касательными друг к другу в точке $A$. Поэтому первое отражение было также отражением от образующей и поэтому отраженный луч должен пройти через фокус образующей, то есть через точку вытекания воды $O$. Точка $O$ находится на траектории, так что точка второго отражения должна быть $O$. В результате двух отражений луч повернулся на $180^\circ$. Это означает, что двойная сумма углов падения равна $180^\circ$ и поэтому $2\alpha+2\beta= 180^\circ$.
Частицы воды, близкие к началу координат еще не достигли огибающей. Частицы, расположенные ниже уровня земли прошли точку касания образующей. Так как частицы образуют непрерывную кривую, на ней должны быть по крайней мере одна точка, находящаяся на образующей.
Есть два способа нахождения точки $P$. Первый способ состоит в следующем. В точке $P$ водяная кривая является касательной к образующей. Следовательно, вертикальная линия, проведенная через \textit{P}, отразится водяной кривой так, что отраженная прямая пройдет через точку $O$. Поэтому мы должны найти методом проб и ошибок такую точку $P$ в верхнем сегменте водяной кривой, что прямая $OP$ и вертикальная прямая, проходящая через \textit{P} образуют равные углы с водяной кривой в точке $P$.
В другом способе можно использовать то, что для любой точки параболы расстояние от фокуса плюс расстояние от горизонтальной линии постоянно. Поэтому для произвольной точки $Q=(x,y)$ на образующей $y+\sqrt{x^2+y^2}=2H$, где $H$ — постоянная, а для каждой точки, расположенной ниже образующей, $y+\sqrt{x^2+y^2} < 2H$. Следовательно, среди точек на водяной кривой точка $P$ имеет наибольшее значение величины $y+\sqrt{x^2+y^2}$. Можно оценить величину $y+\sqrt{x^2+y^2}$ для ряда точек на кривой и выбрать с приемлемой точностью точку с максимальной данной величиной.
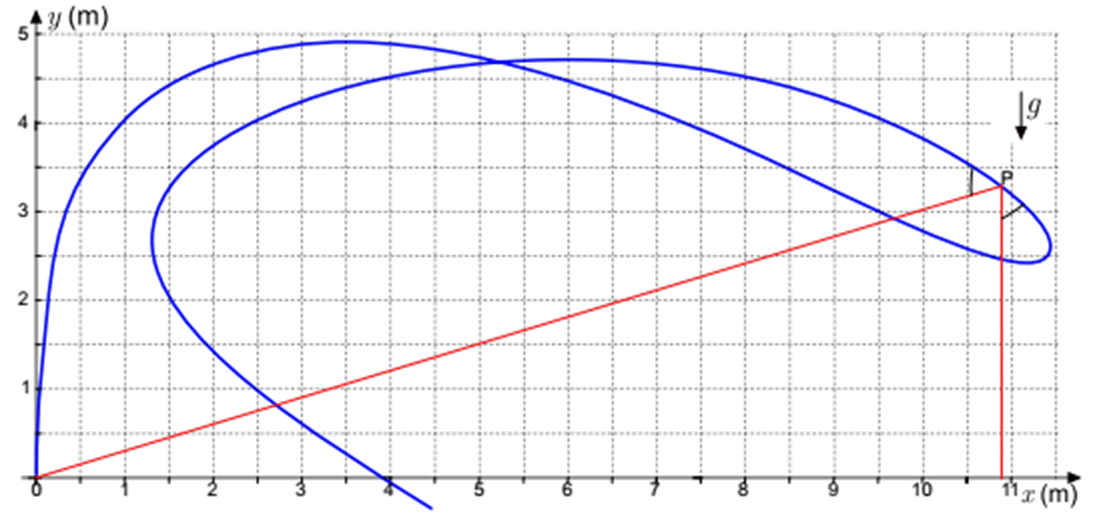
Если мы нашли точку $P$, мы можем легко найти высоту верхней точки огибающей, используя уравнение $y+\sqrt{x^2+y^2}=2H_P$: для верхней точки $x=0$, так что $2y = 2H_P$, следовательно $y=H_P$. Верхняя точка огибающей достигается частицами воды, запущенными вертикально, так что $v^2=2gH_P, v=\sqrt{2gH_P}$. Из рисунка можно получить $2H_P=\left(3.3+\sqrt{{10.8}^2+\ {3.3}^2}\right)~м\approx 14,6~м$, так что $v\approx 12~м/с$.