Часть A. Заряженная пластина в конденсаторе.

Посередине между одинаковыми незаряженными металлическими обкладками плоского конденсатора с площадью $S$ и расстоянием между ними $d\ll{\sqrt{S}}$ находится такая же по форме диэлектрическая пластина массы $m$, заряженная равномерно по поверхности зарядом $q>0$. Обкладки конденсатора подключили к источнику постоянного напряжения $\mathcal{E}$ с нулевым внутренним сопротивлением. Затем пластину отпускают. При движении пластины обкладки конденсатора остаются неподвижными.
Обозначим за $x$ отклонение пластины от начального положения, за $q_1$ — заряд левой обкладки, а за $q_2$ — заряд правой обкладки.

A1 Выразите заряды обкладок конденсатора $q_1(x)$ и $q_2(x)$ через $\mathcal{E}$, $S$, $d$, $q$, $x$ и физические постоянные.

S

A2 Выразите силу электростатического взаимодействия $F(x)$ пластины с обкладками через $\mathcal{E}$, $S$, $d$, $q$, $x$ и физические постоянные.

S

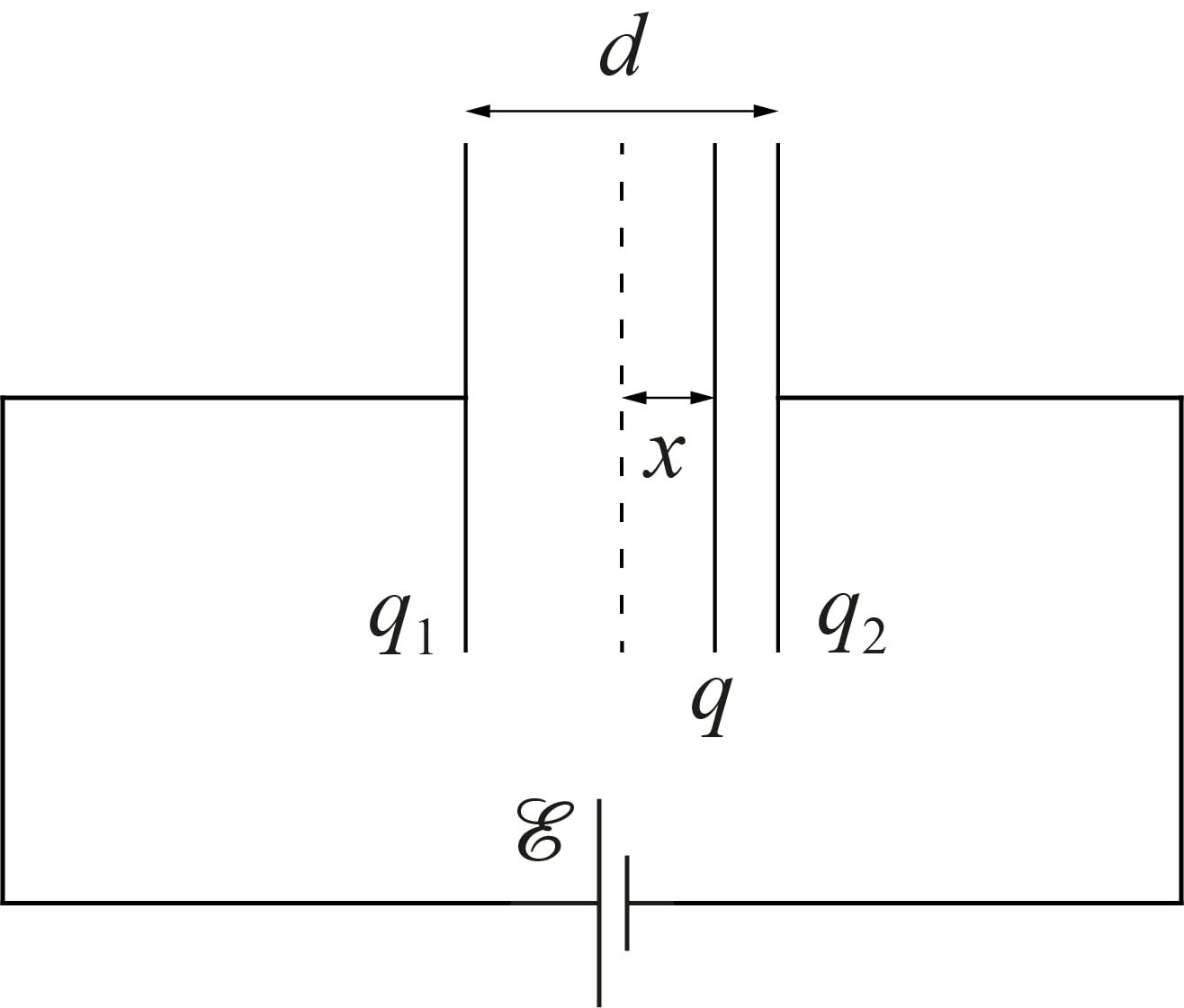
Можно показать, что зависимость смещения пластины $x(t)$ от времени имеет следующий вид
$$x(t)=Ae^{at}+Be^{-at}+C,
$$
где $a$ зависит только от $\mathcal{E}$, $S$, $d$, $q$ и $m$, а $A$, $B$ и $C$ определяются начальными условиями.

A3 Выразите $a$, $A$, $B$ и $C$ через $\mathcal{E}$, $S$, $d$, $q$, $m$ и физические постоянные.

S

A4 Выразите скорость пластины $v^*$ в момент удара об обкладку конденсатора через $\mathcal{E}$, $S$, $d$, $q$, $m$ и физические постоянные.

S

Часть B. Конденсатор с диэлектриком

Плоский конденсатор с площадью обкладок $S$ и расстоянием между ними $d\ll{\sqrt{S}}$ заполнен диэлектриком с диэлектрической проницаемостью $\varepsilon$ и удельным сопротивлением $\rho$. Диэлектрик и обкладки имеют хороший электрический контакт. Пусть разность потенциалов между обкладками конденсатора равна $V$.

B1 Найдите заряды $q$ на металлических обкладках конденсатора. Ответ выразите через $V$, $S$, $d$, $\varepsilon$ и физические постоянные.

S

B2 Найдите силу тока $I$, протекающего через диэлектрик. Ответ выразите через $V$, $S$, $d$, $\rho$ и физические постоянные.

S

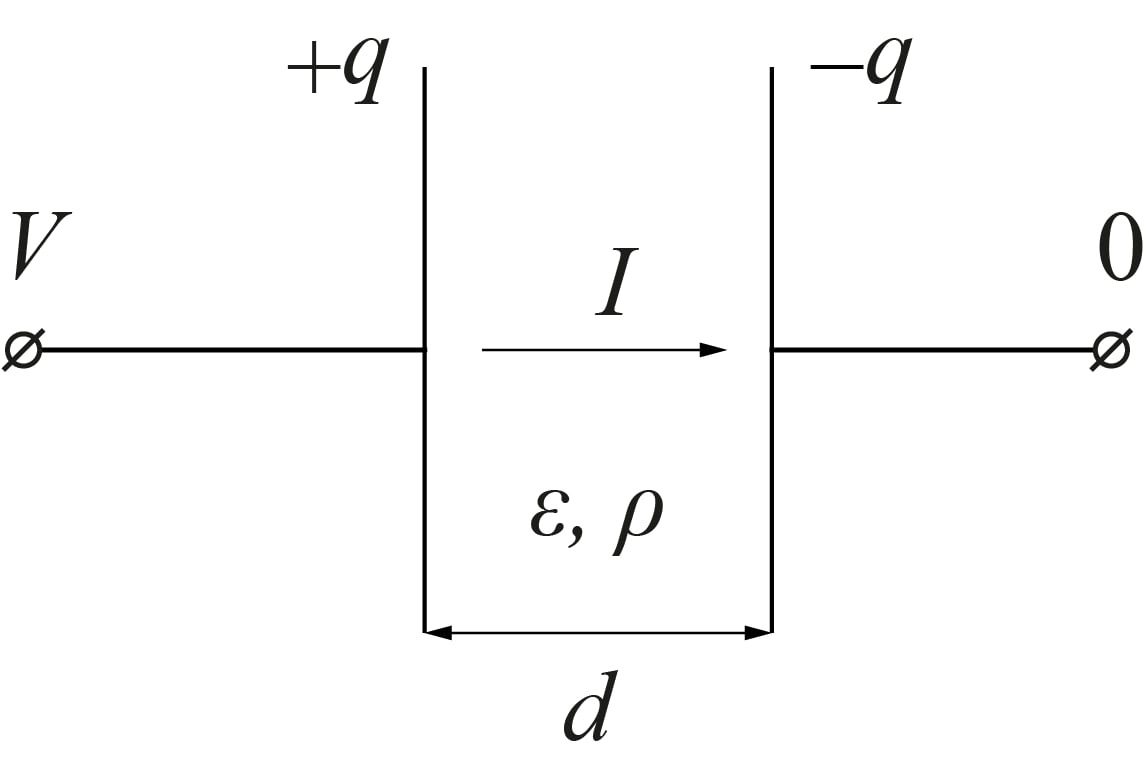
Из двух предыдущих пунктов следует, что схема такого конденсатора в электрической цепи эквивалентна некоторому соединению резистора с сопротивлением $R$ и конденсатора с емкостью $C$.

B3 Найдите $R$ и $C$, а также укажите вид соединения данных элементов (последовательно или параллельно).

S

Теперь сложный конденсатор подключается к источнику постоянного напряжения $\mathcal{E}$, имеющему внутреннее сопротивление $r$. В начальный момент времени конденсатор не заряжен.

B4 Найдите зависимость от времени силы тока $I(t)$, протекающего через источник. Ответ выразите через $\mathcal{E}$, $r$, $R$, $C$ и $t$.

S

Часть C. Конденсатор с двумя диэлектриками

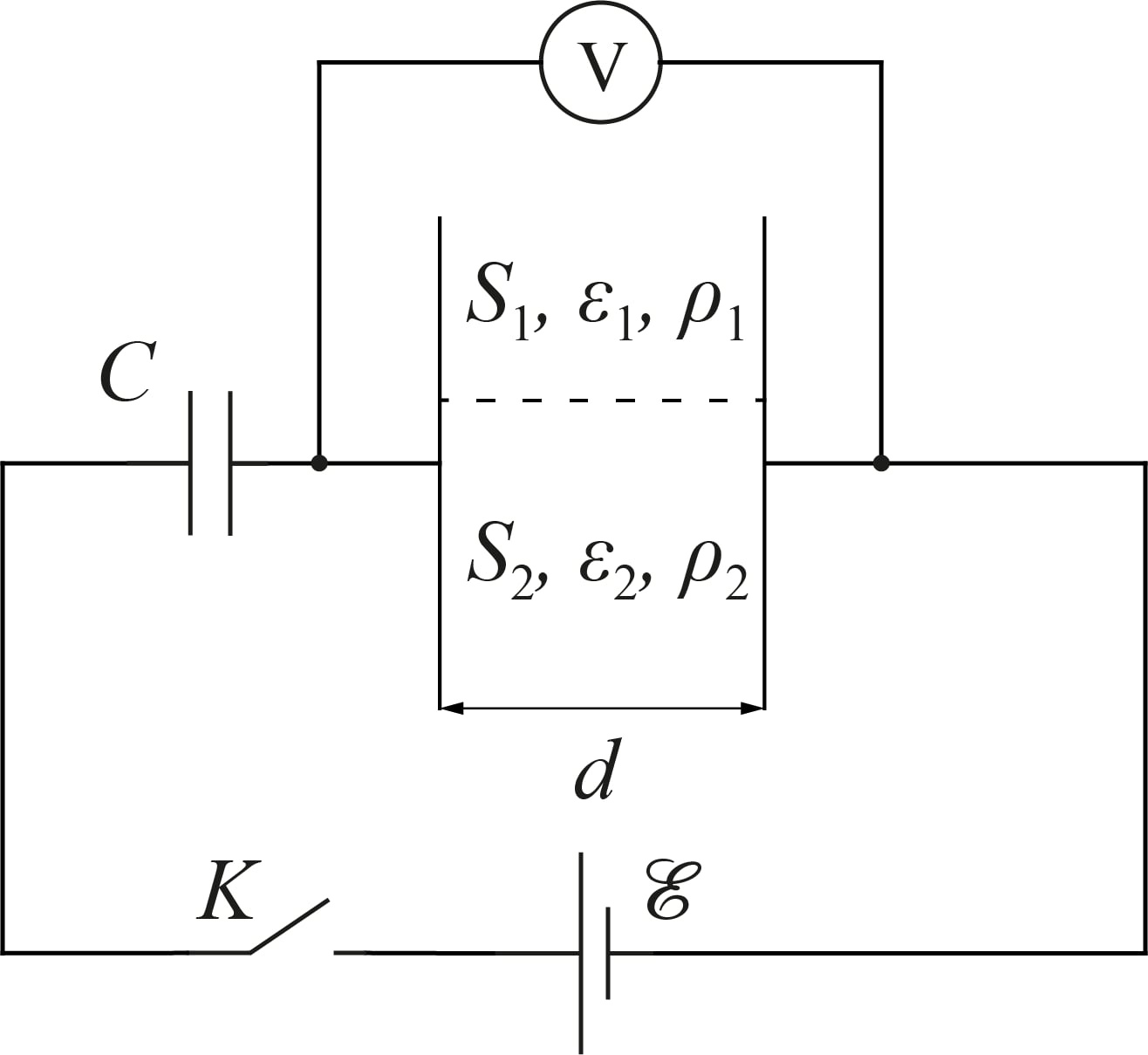
Плоский конденсатор с расстоянием между обкладками $d$ заполнен двумя диэлектриками. Один — с диэлектрической проницаемостью $\varepsilon_1$, удельным сопротивлением $\rho_1$ и площадью контакта с обкладками $S_1$, а другой — с диэлектрической проницаемостью $\varepsilon_2$, удельным сопротивлением $\rho_2$ и площадью контакта с обкладками $S_2$. Оба диэлектрика имеют хороший электрический контакт с обкладками конденсатора.

C1 Найдите эквивалентную ёмкость $C_0$ данного конденсатора. Ответ выразите через $S_1$, $S_2$, $\varepsilon_1$, $\varepsilon_2$, $d$ и физические постоянные.

S

C2 Найдите эквивалентное сопротивление $R_0$ данного конденсатора. Ответ выразите через $S_1$, $S_2$, $\rho_1$, $\rho_2$ и $d$.

S

Данный конденсатор последовательно с конденсатором ёмкости $C$ подключают к источнику постоянного напряжения $\mathcal{E}$, имеющему нулевое внутреннее сопротивление. Пока ключ был разомкнут, конденсаторы были не заряжены. Напряжение на сложном конденсаторе измеряется идеальным вольтметром $V$.

C3 Найдите заряд $q_C(0)$ на конденсаторе ёмкости $C$ сразу после замыкания ключа. Ответ выразите через $\mathcal{E}$, $C$ и $C_0$.

S

C4 Найдите зависимость показаний вольтметра $V(t)$ от времени $t$ после замыкания ключа. Ответ выразите через $\mathcal{E}$, $C$, $C_0$, $R_0$ и $t$.

S

C5 Какое количество теплоты $Q_{R_0}$ выделится на сопротивлении $R_0$? Ответ выразите через $\mathcal{E}$, $C$ и $C_0$.

S

$\textit{Примечание}$ :
$$\int\frac{dx}{ax+b}=\frac{1}{a}\ln\left(ax+b\right)+C
$$
$$\int e^{ax}dx=\frac{e^{ax}}{a}+C
$$