
Показатель преломления материала — нелинейная величина, зависящая от длины волны падающего излучения. Эта зависимость может быть ключевым свойством материала при изготовлении простейших спектроскопических приборов (к примеру — призм). В то же время зависимость показателя преломления от длины волны бывает губительна в других оптических приборах, в частности там, где важна точная фокусировка лучей. В последнее время появляется всё больше новых материалов и веществ, оптические свойства которых необходимо исследовать. В этой задаче мы попробуем определить зависимость показателя преломления неизвестной жидкости от длины волны, используя жидкость, для которой эта зависимость уже известна.
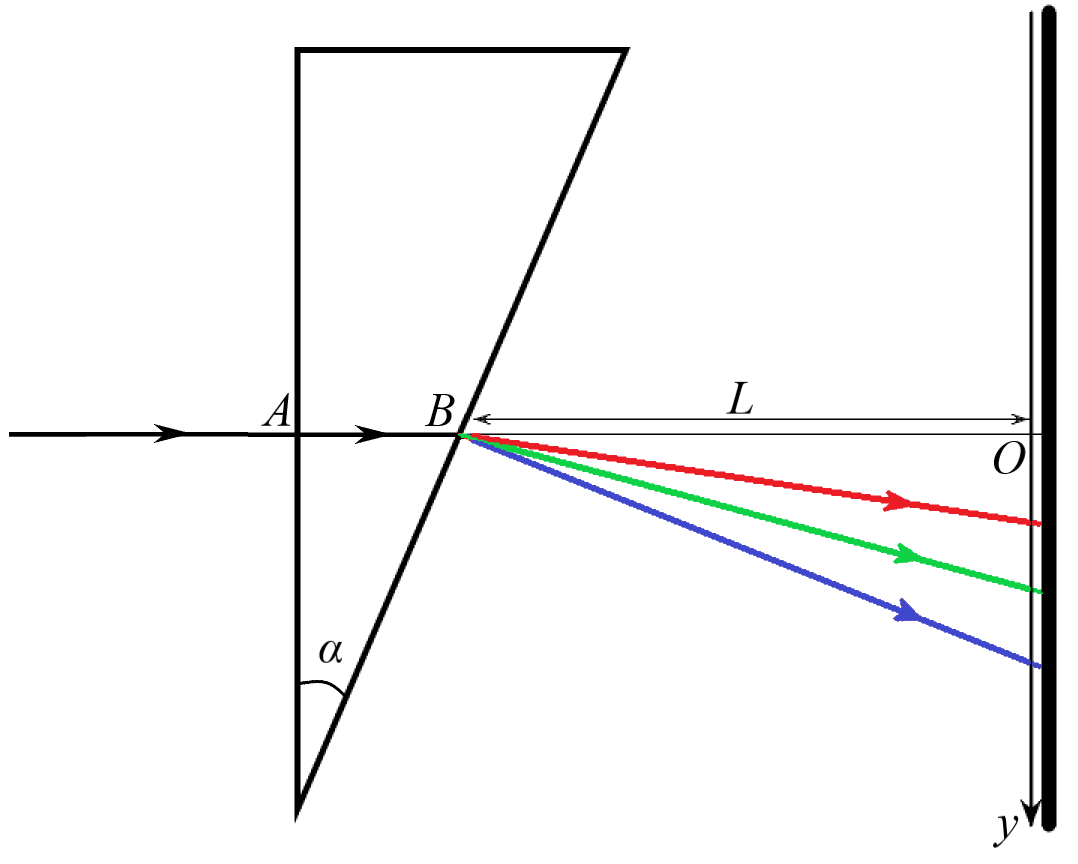
Схема измерений представлена на рисунке ниже. На воздушную призму с тонкими стенками с углом $\alpha=30^{\circ}$ при вершине, погружённую в исследуемую жидкость, падает тонкий луч источника. Луч падает на одну из граней призмы перпендикулярно в точке $A$ и затем выходит из призмы в точке $B$. Из-за зависимости показателя преломления от длины волны углы, под которыми лучи разной длины волны выйдут из призмы, будут различаться. На расстоянии $L$ от точки $B$ находится экран, перпендикулярный $AO$. Для удобства дальнейшей работы введём безразмерную величину $x=\frac yL$. На экране размещено множество светочувствительных элементов, которые измеряют интенсивность $\mathcal J_x(x)$ (мощность, падающую на единицу площади поверхности в единицу времени) в точках, в которых они расположены.
Обычный источник света (такой как настольная лампа) характеризуется тем, что излучает свет не одной длины волны (как это делает лазер), а длин волн сразу в некотором диапазоне. Чтобы охарактеризовать его излучение, введём понятие спектральной плотности $\mathcal J_\lambda(\lambda)$. Мы определяем её так, чтобы мощность, излучаемая источником в диапазоне длин волн от $\lambda$ до $\lambda+\Delta\lambda$, равнялась $\mathcal J_\lambda(\lambda)\Delta\lambda$, где $\Delta\lambda$ — малая величина. В этой части задачи мы исследуем спектральную плотность источника.
Выясним сначала, в какую точку $x$ на экране должен попадать луч, проходящий через призму, в зависимости от показателя преломления жидкости. Применив закон Снеллиуса для лучей получим следующую формулу для зависимости $x$ от $n$:\[x=\operatorname{tg}\alpha\frac{\sqrt{n^2-\sin^2\alpha}-\cos\alpha}{\sqrt{n^2-\sin^2\alpha}+\sin\alpha\operatorname{tg}\alpha}.\tag{1}\]Чтобы по известному значению $x$ восстановить значение $n$, формулу (1) необходимо "обратить". В результате несложных вычислений получим:\[n=\frac{\sqrt{1+x^2}}{1-x\operatorname{ctg}\alpha}.\tag{2}\]Показатель преломления большинства прозрачных материалов в видимом диапазоне можно приближённо описать формулой:\[n(\lambda)=A+\frac B{\lambda^2},\tag{3}\]где $A$ и $B$ — некоторые постоянные.
Сначала измерения проводят в известной жидкости, для которой эти постоянные равны $A=1.14$ и $B=8.6\cdot10^4~нм^{2}$. В таблице в листе ответов приведены значения интенсивности $\mathcal J_x$ в условных единицах в точках с координатой $x$.
Чтобы получить формулу для спектральной плотности $\mathcal J_\lambda$, необходимо провести более сложные расчёты. Ограничимся здесь лишь итоговой формулой для спектральной плотности:\[\mathcal J_\lambda=\frac{2B\sqrt{1+x^2}}{\lambda^3}\frac{(1-x\operatorname{ctg}\alpha)^2}{x+\operatorname{ctg}\alpha}\mathcal J_x.\tag{4}\]
В дальнейшем нам также понадобится посчитать, какая доля мощности источника излучается на длинах волн, меньших некоторого значения $\lambda$. Обозначим эту величину как $\sigma(\lambda)$. Для её нахождения надо посчитать площадь под графиком $\mathcal J_x$. Это мы будем делать методом трапеций.
Пусть нам известны значения $f_i$ функции $f(x)$ в точках $x_i$. Тогда площадь под графиком этой функции можно оценить как сумму площадей трапеций, построенных, как показано на рисунке ниже.
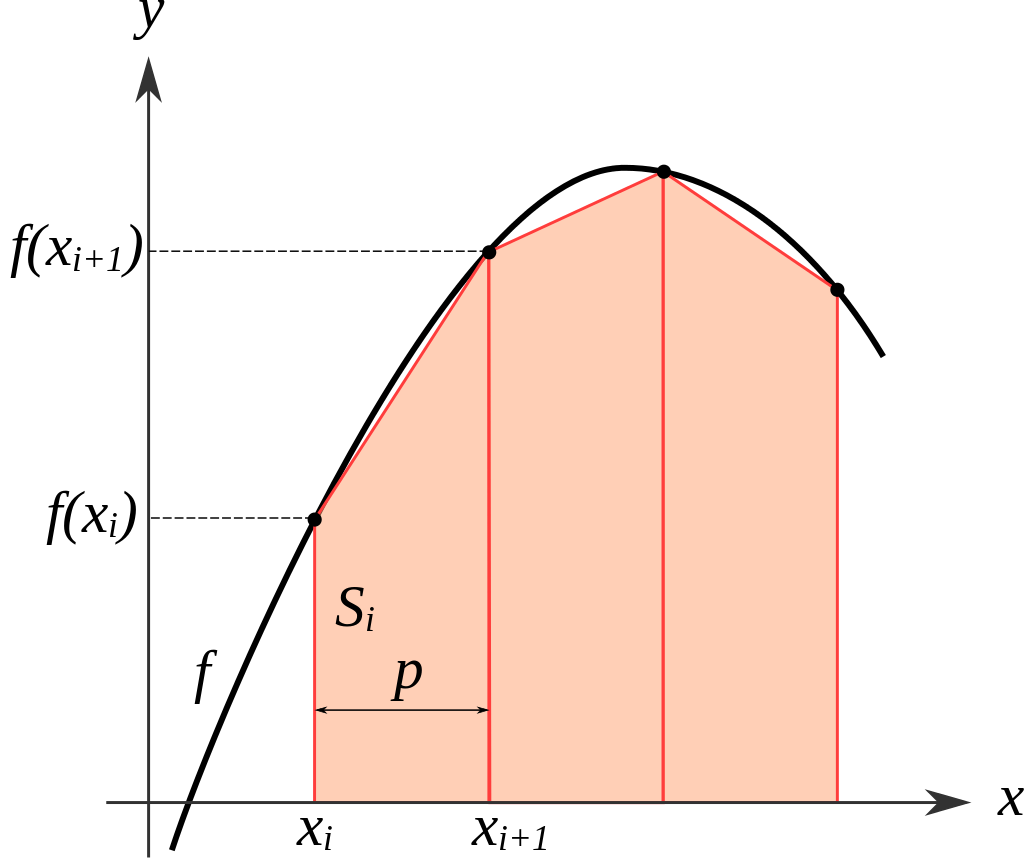
Поскольку в нашем случае точки $x_i$ расположены через равные интервалы, формула для итоговой площади $S_k$ под графиком между точками $x_0$ и $x_k$ имеет вид:\[S_k\approx\left(\frac{f_0+f_k}2+\sum_{i=1}^{k-1}f_i\right)\Delta x,\tag{5}\]где $\Delta x=x_{i+1}-x_i$ — расстояние между соседними точками.
Теперь жидкость, в которую погружена призма, заменим на неизвестную, зависимость показателя которой от длины волны мы хотим найти. Схема эксперимента остаётся той же. В таблице в листе ответов приведены значения интенсивности $\mathcal J_x$ в условных единицах в точках с координатой $x$.
В прошлой части задачи мы получили зависимость $\sigma(\lambda)$, которая теперь позволит нам восстановить $n(\lambda)$ для неизвестной жидкости. Однако значения $\sigma$, полученные в предыдущей части, не совпадают со значениями, полученными здесь. Чтобы узнать, каким значениям $\lambda$ соответствуют полученные в предыдущем пункте $\sigma$, прибегнем к т.н. линейной интерполяции зависимости $\lambda(\sigma)$.
Суть линейной интерполяции состоит в следующем. Пусть нам известны значения $\lambda_1$ и $\lambda_2$ функции $\lambda(\sigma)$ в точках $\sigma_1$ и $\sigma_2$ соответственно. Если эти точки находятся достаточно близко друг к другу, то с хорошей точностью можно приблизить функцию между этими двумя точками участком прямой. Это позволяет нам приближённо восстановить значения функции для $\sigma_1 < \sigma < \sigma_2$.
Выведем формулу, определяющую $\lambda(\sigma)$. Поскольку функцию мы приближаем линейной, то искомую зависимость можно записать в виде:\[\lambda=a\sigma+b.\tag{6}\]Для нахождения $a$ и $b$ заметим, что эта прямая должна проходить через точки $(\sigma_1,\lambda_1)$ и $(\sigma_2,\lambda_2)$. Подставляя их в уравнение (6), получим систему уравнений:\[\begin{cases}\lambda_1=a\sigma_1+b,\\\lambda_2=a\sigma_2+b.\end{cases}\tag{7}\]Решая эту систему, получим окончательно:\[\lambda=\frac{\lambda_2-\lambda_1}{\sigma_2-\sigma_1}\sigma+\frac{\lambda_1\sigma_2-\lambda_2\sigma_1}{\sigma_2-\sigma_1}.\tag{8}\]