
|
A1. 1
Получен правильный ответ:
$$I_{bR}=\cfrac{nSe}{\tau}=0{,}96~\text{мкА}/\text{мм}^2 $$ |
0.50 |
|
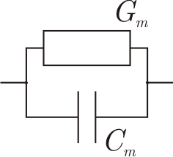
| B1. 1 В схеме конденсатор $C_m$ и резистор $G_m$ соединены параллельно. | 0.20 |
|
|
B1. 2
Правильно нарисована одна схема (рис.1.)
|
0.20 |
|
|
B1. 3
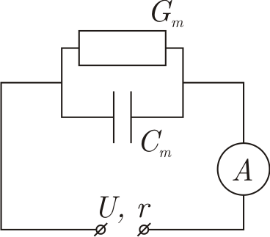
Правильно нарисована вторая схема (рис.2.)
|
0.10 |
|
| B2. 1 Сила тока через амперметр $I=GU+C\dot{U}$, где $U$ - напряжение на конденсаторе и резисторе. | 0.30 |
|
| B2. 2 По графику видно, что сила тока в установившемся режиме постоянна, поэтому, $GU$ можно пренебречь. | 0.10 |
|
| B2. 3 Переходные процессы достаточно короткие, поэтому, $r\ll{1/G}$, и всё напряжение падает на конденсаторе. | 0.20 |
|
| B2. 4 Из графика $dU/dt=2~\text{мВ}/\text{с}$. | 0.20 |
|
|
B2. 5
Получен правильный ответ:
$$C_m=I\left(\cfrac{dU}{dt}\right)^{-1} $$ |
0.20 |
|
|
B3. 1
Получена правильный ответ в общем виде:
$$G_m=\cfrac{I}{U} $$ |
0.30 |
|
|
B3. 2
Получено верное численное значение:
$$G_m=0{,}1~\text{нСм} $$ |
0.20 |
|
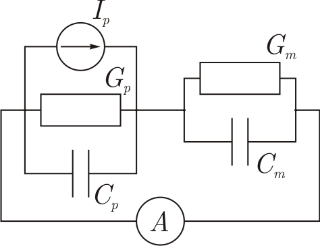
| C1. 1 Мембраны соединены последовательно | 0.10 |
|
| C1. 2 Между мембранами включен амперметр | 0.10 |
|
|
C1. 3
Нарисована верная схема (рис.3.)
|
0.30 |
|
|
C2. 1
Сила тока через амперметр
$$I=I_p+G_pU_p+C_p\cdot{dU_p/dt} $$ |
0.20 |
|
|
C2. 2
Сила тока через амперметр
$$I=G_mU_m+C_m\cdot{dU_m/dt} $$ |
0.20 |
|
|
C2. 3
Связь напряжений:
$$U_p+U_m=0 $$ |
0.20 |
|
| C2. 4 Получено правильное дифференциальное уравнение. | 0.30 |
|
| C2. 5 Получено общее решение дифференциального уравнения. | 0.40 |
|
|
C2. 6
Учтены начальные условия и получен верный ответ:
$$I(t)=I_p\left(\cfrac{G_m}{G_m+G_p}+\left(\cfrac{C_m}{C_m+C_p}-\cfrac{G_m}{G_m+G_p}\right)\cdot{e^{-\gamma t}}\right){,}\quad\text{где}\quad\gamma=\frac{G_m+G_p}{C_m+C_p} $$ |
0.70 |
|
|
C3. 1
Получено верное выражение в общем виде:
$$G_p=\gamma\cdot{(C_m+C_p)} $$ |
0.30 |
|
|
C3. 2
Получено верное численное значение:
$$G_p=100~\text{нСм} $$ |
0.20 |
|
|
C4. 1
Получен ответ и сделан правильный вывод:
$$\cfrac{G_m}{G_p}=1000\gg{1} $$ |
0.20 |
|
|
C5. 1
Получено верное выражение:
$$I_p=I(0)\cdot{\cfrac{C_m+C_p}{C_m}} $$ |
0.30 |
|
|
C5. 2
Получен численный ответ:
$$I_p=48~\text{нА} $$ |
0.20 |
|
|
C6. 1
Записано выражение, связывающее $I_p$, $I_{bR}$ и $\alpha$:
$$\alpha=\cfrac{1}{2}\left(1+\cfrac{I_p}{I_{bR}}\right) $$ |
0.20 |
|
|
C6. 2
Получено верное численное значение:
$$\alpha=0{,}525 $$ |
0.10 |
|
|
D1. 1
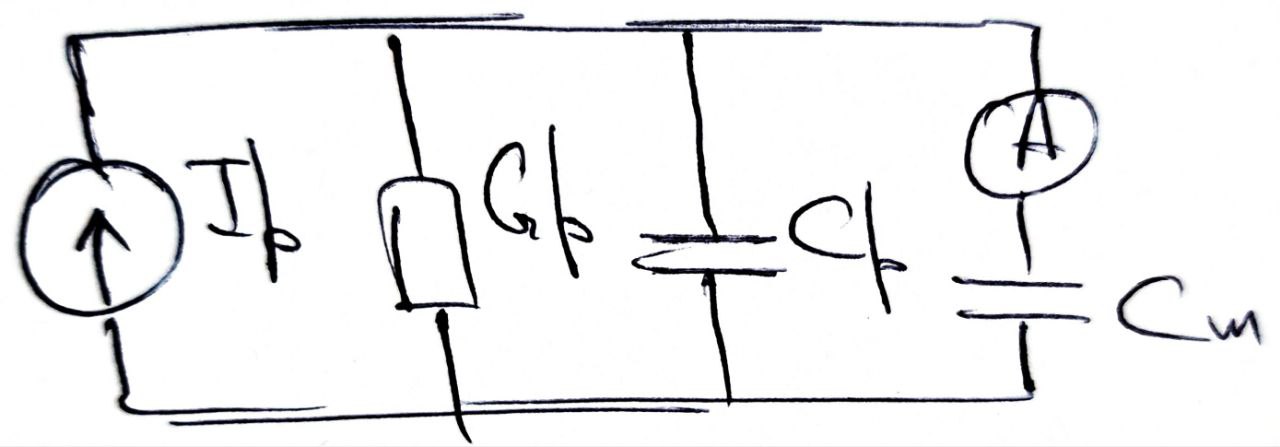
Нарисована верная схема
|
0.20 |
|
|
D2. 1
Сила тока через амперметр:
$$I=C_m\cdot{\cfrac{dU_m}{dt}}=-C_m\cdot{\cfrac{dU_p}{dt}} $$ |
0.10 |
|
|
D2. 2
Выражение для $U_p$:
$$U_p=-\cfrac{1}{C_m}\cdot{\int\limits_0^{t}I(t)dt} $$ |
0.20 |
|
|
D2. 3
Сила тока через амперметр:
$$I=I_p+G_pU_p-I\cdot{\cfrac{C_p}{C_m}} $$ |
0.10 |
|
|
D2. 4
Получен правильный ответ:
$$I_p(t)=\cfrac{C_m+C_p}{C_m}\cdot{I(t)}+\cfrac{G_p}{C_m}\cdot{\int\limits_0^{t}I(t)dt} $$ |
0.60 |
|
D3. 1
|
None |
|
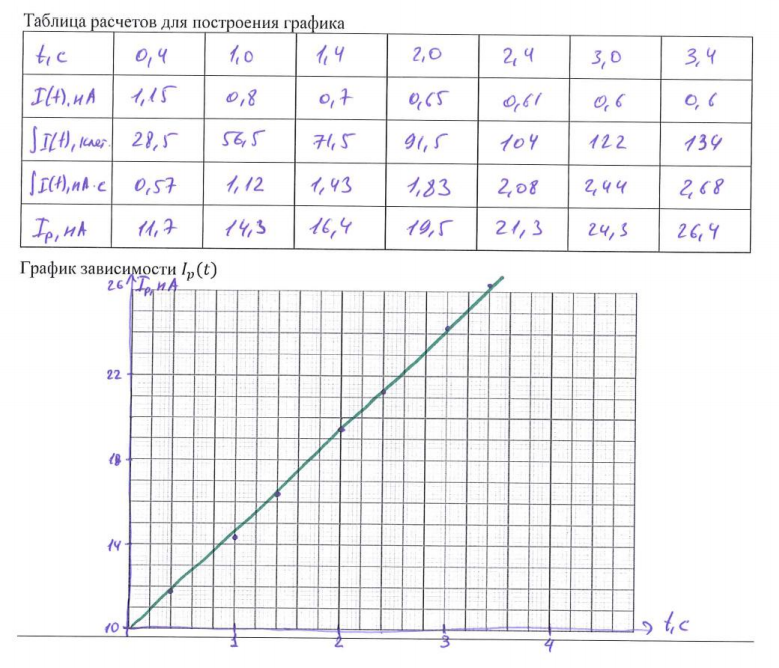
| D3. 2 Таблица значений силы тока $I(t)$ (рис.5.) | 0.10 |
|
| D3. 3 Таблица значений $q(t)=\displaystyle\int\limits_0^{t}I(t)dt$ (рис.5.) | 0.40 |
|
| D3. 4 График $I_p(t)$ (рис.5.) | 0.80 |
|
| E1. 1 Построен качественный график - значение стационарной силы тока сравнимо с начальной силой тока. | 0.50 |
|
|
E1. 2
Верный выражение для стационарной силы тока:
$$I_\text{ст}=I_p\cdot{\cfrac{G_m}{G_m+G_p}} $$ |
0.10 |
|
|
E1. 3
Верный численный ответ:
$$I_\text{ст}=24~\text{нА} $$ |
0.40 |
|