
Кольцевой резонатор изготовлен из одного кольцевого одномодового волновода, соединенного с двумя прямолинейными одномодовыми волноводами (см. рис.). В одномодовом волноводе распространение света одномерное: фаза электрического и магнитного поля в любом сечении волновода — постоянны. Соединения $A$ и $C$ между кольцевым и прямолинейным волноводами устроены таким образом, что только небольшая часть $\alpha\ll 1$ энергии, распространяющейся в одном из волноводов, передается через соединение в другой волновод. Оба соединения можно считать одинаковыми.
Если в кольцевом волноводе распространяется волна амплитуды $E$, то из-за нелинейности среды возникает генерация второй гармоники: волны на удвоенной частоте с амплитудой $\mathcal E$ (эта волна уже распространяется линейно, не образуя волны на учетверенной частоте). Дисперсия отсутствует, т.е. коэффициент преломления одинаков как для основной волны, так и для второй гармоники. Т.е. увеличение амплитуды $\Delta\mathcal E$ второй гармоники пропорционально пройденному расстоянию.
Введем величину, описывающую нелинейность волновода: коэффициент $\delta$. Определим его следующим образом: если волна амплитуды $E$ проходит полукруг $ABC$, амплитуда $\mathcal E$ второй гармоники увеличивается на $\Delta\mathcal E=\delta E^2$. Это справедливо, если $\delta E\ll 1$ (это можно считать заданным).
Коэффициент связи $\alpha$ является функцией частоты волны. Для основной волны этот коэффициент равен $\alpha$, для второй гармоники — $\alpha^2$.
Длина кольцевого волновода равна целому числу длин волн основной волны.
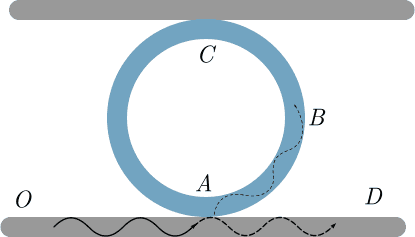
Лазерное излучение интенсивности $I_0=E_0^2$ ($E_0$ — амплитуда волны) и очень большой длины когерентности направляется на вход $O$ в нижний прямолинейный волновод. На выходе $D$ наблюдается основная волна и вторая гармоника. Для фиксированных значений $I_0$ и $\delta$ интенсивность второй гармоники $\mathcal I$ на выходе зависит от коэффициента связи $\alpha$, который легко задается при изготовлении резонатора.