
Если изолированная планета шарообразной формы покрыта тонким слоем жидкости, форма поверхности жидкости будет стремиться к сферической в силу принципа минимума потенциальной энергии.
Если же рядом с планетой есть другие тела, они будут искажать форму поверхности жидкости. Это связано с приливными силами, которые возникают за счет того, что разные участки жидкости притягиваются этому телу с различными силами. Такие силы являются причиной приливов и отливов на поверхностях планет, почему и получили свое название.
В задаче рассматривается следующая система. Два однородных шарообразных тела (планеты) массами $m$ (малое тело) и $M$ (большое тело, $M>m$) движутся по круговым орбитам вокруг общего центра масс. Расстояние между центрами тел равно $L$, радиус большого тела равен $R$ ($L\gg{R}$), а малое тело можно считать точечным. Поверхность большого тела покрыта тонким слоем жидкости плотность $\rho$, форма поверхности которой является объектом изучения.
Вам предстоит определить форму поверхности большого тела при синхронном вращении, когда угловая скорость орбитального вращения тел совпадает с угловой скоростью вращения большого тела вокруг собственной оси. Далее вам нужно описать динамику приливного захвата, то есть процесса перехода к синхронному вращению.
В этой части задачи рассматривается синхронное вращение. Большое тело вращается вокруг своей оси с угловой скоростью, равной угловой скорости орбитального вращения тел $\omega$.
Ответ выразите через $G, m, M$ и $L$.
Перейдём в неинерциальную систему отсчёта, связанную с центром большого тела и вращающуюся так, что центр малого тела в ней неподвижен.
Напомним выражение для ускорения в неинерциальной системе отсчёта с началом в точке $O$, движущимся с ускорением $\vec{a}_0$, координатные оси которой вращаются с угловой скоростью $\vec{\omega}$ и угловым ускорением $\vec{\varepsilon}$:
$$\vec{a}_\text{отн}=\vec{a}-\vec{a}_0+\omega^2\vec{r}_\perp-\big[\vec{\varepsilon}\times\vec{r}\big]-2\big[\vec{\omega}\times\vec{v}_\text{отн}\big].
$$
Здесь $\vec{a}$ — ускорение в инерциальной системе отсчёта, $\vec{r}_\perp$ — компонента радиус-вектора частицы, перпендикулярная оси вращения, а $\vec{v}_\text{отн}$ — скорость частицы относительно неинерциальной системы отсчёта.
Во всех пунктах задачи ограничивайтесь только первыми тремя слагаемыми:
$$\vec{a}_\text{отн}\approx{\vec{a}-\vec{a}_0+\omega^2\vec{r}_\perp}.
$$
Задача является плоской, поэтому считайте, что $\vec{r}_\perp=\vec{r}$, если обратное не оговорено.
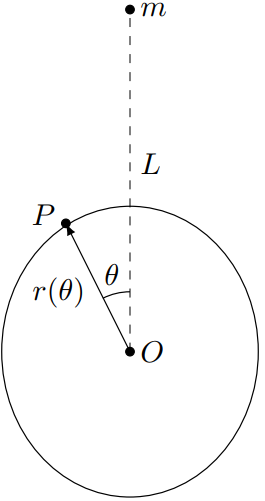
Представим форму поверхности в виде $r(\theta)=R+h(\theta)$, где $h(\theta)\ll{R}$, а $h(\pi/2)=0$.
Примечание: воспользуйтесь следующим приближением: $$\cfrac{1}{\sqrt{1+a^2-2a\cos\theta}}\approx{1+a\cos\theta+\cfrac{a^2(3\cos^2\theta-1)}{2}} $$
Мы рассмотрели поведение системы в установившемся режиме. Далее будем изучать переходные процессы, которые приводят к выравниваю угловых скоростей орбитального движения и вращения большого тела вокруг своей оси.
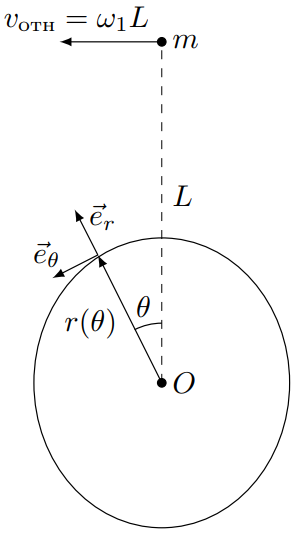
Примечание: воспользуйтесь результатами, полученными при решении пункта $\mathrm{A4}$.
Из закона изменения момента импульса для элемента поверхности жидкости можно получить, что его уравнение движения эквивалентно уравнению вынужденных колебаний:
$$\Delta{m} R^2 \left(\ddot{\theta}+2\gamma\dot{\theta}+\omega^2_0(\theta-\theta_0)\right)=F_\tau(t{,}\,\theta)R,
$$
где $\gamma$ и $\omega_0$ — постоянные величины, $\theta_0$ — положение элемента жидкости в равновесии.
Считайте, что $\omega_0\gg{\sqrt{Gm/L^3}}$.
Во всех пунктах считайте, что $\theta - \theta_0 \ll 1$, поэтому справедливо приближение $F(t,\,\theta) \approx F(t,\, \theta_0)$.
$$\theta(t)=\theta_0+A\sin(2\omega_1t-2\theta_0-\varphi_0)
$$
Найдите $A$ и $\varphi_0$. Ответы выразите через $G$, $m$, $L$, $\gamma$, $\omega_0$, $\omega$, $\Omega$ и $\theta_0$.
Далее для удобства будем использовать угол $\varphi_1 = 2 \theta_0 + \varphi_0$ и записывать выражение для $\theta(t)$ в следующем виде:
$$\theta(t{,}\theta_0)=\theta_0+A\sin(2\omega_1t-\varphi_1)
$$
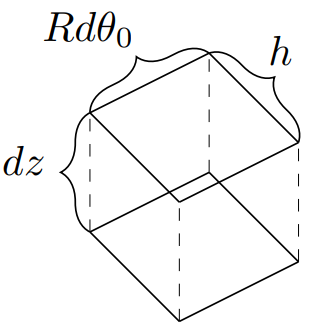
Для поиска момента сил, действующих на большое тело, потребуется рассмотреть произвольное сечение большего тела. Будем отсчитывать угол $\beta$ от оси вращения большего тела. Тогда радиус сечения большего тела в перпендикулярной плоскости равен $r=R\sin\beta$. Считайте, что для описания зависимости $\theta(t{,}\,\theta_0{,}\,\beta)$ и $h'(t{,}\,\theta_0{,}\,\beta)$ достаточно везде заменить радиус $R$ на расстояние до оси вращения $R\sin\beta$.
Приливным захватом называют выравнивание угловых скоростей орбитального вращения и вращения вокруг собственной оси. В этой части задачи вам предстоит определить параметры $\omega_0$ и $\gamma$ для модели, рассмотренной в части B, а также оценить время, в течении которого происходит приливной захват в системе Земля-Луна.
Считайте известными следующие данные:
Примечание: при синхронном вращении моментом импульса Земли, связанным с вращением вокруг ее оси, можно пренебречь.
Найдите величину среднего углового ускорение Земли $\dot{\Omega}_0$.
Выразите ответ через $m$,$M$, $R$, $G$, $L_0$, $\Omega_0$, $\dot{L}_0$ и найдите его численное значение.
Для описания переходного процесса необходимы численные значения параметров $\omega_0$ и $\gamma$. Для их определения считайте известным следующее:
Сравните его со значением $\dot{\Omega}_0$, полученным в пункте $\mathrm{C2}$ и сделайте вывод о применимости рассматриваемой модели (считайте модель применимой, если $\Omega_0$ и $\Omega_{0\text{(мод)}}$ отличаются не более, чем в 10 раз).
Приливной захват в системе Земля-Луна можно разделить на два этапа: