Введение

Доведение идеи квантовых вычислений до прикладных разработок — одна из важных задач современных науки и технологий. Один из подходов к решению этой задачи — управление одиночными электронами в транзисторах с помощью переменных электромагнитных полей. В этой задаче мы разберемся, как с помощью одноэлектронных транзисторов и рефлектометрии можно считать состояние квантового бита информации в прототипах квантовых компьютеров. В частях А и B обсуждается распространение радиоволн вдоль проводов и линий электропередач. В части С рассматриваются условия отражения волн. В части D описывается одноэлектронный транзистор, а в части E и F обсуждается метод рефлектометрии.

Часть A. Модель коаксиального провода (2 балла)

Когда рассматривается постоянный ток или низкочастотные сигналы, предполагается, что он распространяется по цепи мгновенно. Такое предположение верно, если длина волны таких сигналов много больше размеров цепи. Но когда рассматриваются радиоволны, распространение становится более сложным, и нужно учитывать емкость и индуктивность проводов. В этой задаче считайте, что электрическое и магнитное поле перпендикулярны оси провода (так называемая поперечная электромагнитная мода).

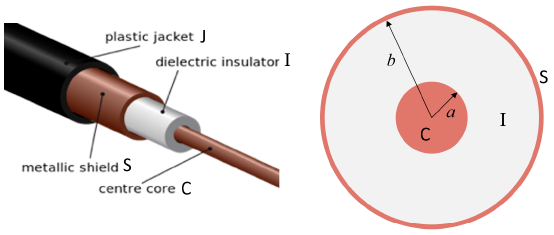
В проводе центральная медная жила радиуса $a$ окружена медной оплеткой внутреннего радиуса $b$ (рис. 1). Между ними находится диэлектрик (диэлектрическая проницаемость $\varepsilon_r$, магнитная проницаемость $\mu_r$). Сопротивлением меди можно пренебречь. Когда электромагнитный сигнал распространяется в проводе, он ограничен центральной жилой и внешней оплеткой.

A1  ^0.20 С какой скоростью распространяются электромагнитные волны в коаксиальном проводе?

A2  ^0.20 Пусть участок центральной жилы длиной $\Delta x$ заряжен зарядом $\Delta q$, а внешняя оплетка заземлена. Найдите электрическое поле между центральной жилой и оплеткой.

A3  ^0.30 Найдите емкость $C_x$ единицы длины коаксиального провода.

A4  ^0.30 Найдите индуктивность $L_x$ единицы длины провода.

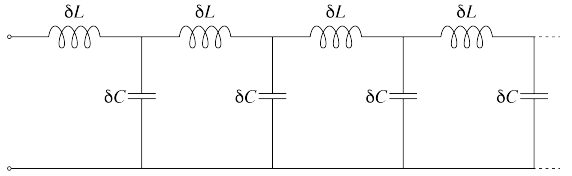
Кабель целиком можно представить как емкости и индуктивности его малых участков. Будем считать, что индуктивность провода — это характеристика центральной жилы, а емкости характеризуют диэлектрик между проводниками (рис. 2).

A5  ^1.00

1. Покажите, что импеданс $Z_0$ полубесконечного провода равен $Z_0=\sqrt{L_x/C_x}$.
2. Рассчитайте численное значение $b/a$, если импеданс провода $Z_0=50\ \Omega$, а параметры диэлектрика --- $\varepsilon_r=4.0$ и $\mu_r=1.0$.

Часть B. Линия электропередачи (1 балл)

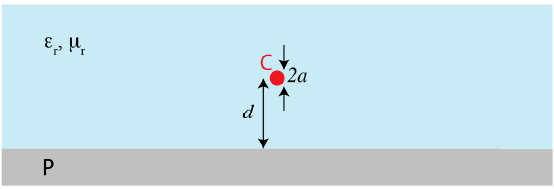
Рассмотрим одну из возможных реализаций линии электропередачи. Сигнал передается по очень тонкому проводнику радиуса $a$, который находится на расстоянии $d\gg a$ от заземленной хорошо проводящей плоскости (рис. 3). Вещество, окружающее проводник, обладает диэлектрической проницаемостью $\varepsilon_r$ и магнитной проницаемостью $\mu_r$. Обратно ток течет по заземленной плоскости.

B1  ^1.00 Найдите импеданс такой линии электропередачи.

Часть C. Основы рефлектометрии (1.2 балла)

Электромагнитная волна может распространяться по линии в двух противоположных направлениях. Для обоих направлений импеданс $Z_0$ связывает амплитуду напряжения $V_0$ и тока $I_0$ как $Z_0=V_0/I_0$. Рассмотрим соединение двух линий с импедансами $Z_0$ и $Z_1$ (рис. 4).

Когда сигнал амплитуды $V_i$, распространяющийся в линии с импедансом $Z_0$, достигает места соединения, он частично проходит во вторую линию и распространяется дальше (амплитуда прошедшего сигнала $V_t$), а частично отражается и распространяется в обратном направлении в той же линии, что и исходный сигнал (амплитуда отраженного сигнала $V_r$).

C1  ^1.00 Найдите коэффициент отражения $\Gamma=V_\text{r}/V_\text{i}$ в месте соединения линий.

C2  ^0.20 Укажите условие(я), при которых фаза исходного сигнала $V_i$ изменяется на $\pi$ при отражении.

Часть D. Одноэлектронный транзистор (3.3 балла)

Упрощенная схема одноэлектронного транзистора (single electron transistor, SET) представлена на рисунке 5. Квантовая точка (quantum dot, QD) — малый изолированный проводник и поблизости расположенные электроды. На квантовой точке могут накапливаться электроны, попадающие на нее туннельными переходами через электроды S и D на схеме. Затвор G — контакт QD с третьим электродом — эквивалентен конденсатору, указанному на схеме (рис. 5).

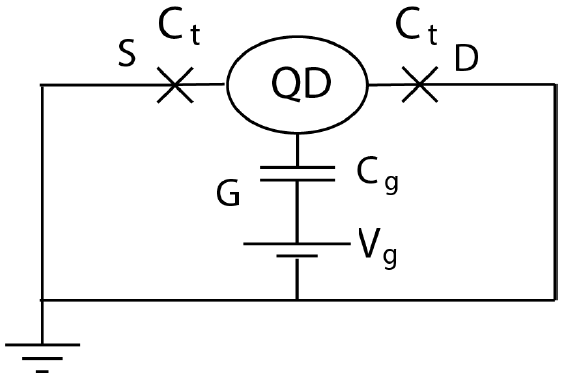
Емкостью $C_t$ туннельных переходов можно пренебречь и считать емкость $C_g$ затвора полной емкостью квантовой точки. В данной части задачи потенциал на электродах S и D поддерживается нулевым, а на затворе — равным $V_g$.

D1  ^1.50

Пусть QD содержит $n$ электронов.

1. Найдите потенциал $\varphi_n$ на QD.
2. Найдите энергию $\Delta E_n$, которая необходима еще одному электрону для попадания на QD.

При $\Delta E_n <0$ электроны перетекают на QD, пока их количество не достигнет такого $\mathcal{N}> n$, что $\Delta E_{\mathcal{N}} \ge 0$. Соответствующие этому равновесию число $\mathcal{N}$ и добавочную энергию $\Delta E_{\mathcal{N}}$ можно задать, подстраивая значение потенциала $V_g$.

D2  ^0.50 Найдите $E_c=\max \Delta E_{\mathcal{N}}(V_g)$ — максимальную из равновесных добавочных энергий, достижимых подстройкой потенциала $V_g$.

В случае, когда $\Delta E_{\mathcal{N}}=0$, переход электронов на QD не требует дополнительных затрат энергии и SET находится в проводящем состоянии (ON). В другом случае, когда $\Delta E_{\mathcal{N}}>0$, SET проводит ток слабо, т.е. находится в состоянии OFF.

Состояния ON и OFF хорошо различимы, если выполнен ряд условий. Во-первых, тепловой энергии электронов на электродах S и D не должно хватать для перехода на QD.

D3  ^0.50 Найдите, какому условию должна удовлетворять температура электронов, чтобы они не могли перейти на QD.

Во-вторых, туннелирование электронов на QD и обратно ограничивает время жизни энергетических состояний. Туннельный переход можно считать резистором, через который QD разряжается за время, совпадающее с характерным временем туннелирования.

D4  ^0.80

1. Напишите оценку времени туннелирования, используя емкость $C_t$ и сопротивление $R_t$ туннельного перехода.
2. Найдите соотношение, которому должно удовлетворять $R_t$, чтобы состояния ON и OFF не перекрывались.

Часть E. Изучение состояния SET-транзистора с помощью рефлектометрии (1 балл)

Будем считать, что в ON-состоянии SET эквивалентен сопротивлению $R_{\text{ON}}=100 \, \text{k} \Omega$, а в OFF-состоянии является изолятором. Рефлектометрия позволяет определить состояние SET, проведя измерения амплитуды и фазы отраженного от SET сигнала и вычислив коэффициент отражения $\Gamma$.

При переключении SET из состояния ON в состояние OFF коэффициент отражения меняется на

$$\Delta\Gamma = |\Gamma_\text{ON} - \Gamma_\text{OFF}| \ \ ,$$

где $\Gamma_{\text{ON}}$ и $\Gamma_{\text{OFF}}$ — коэффициенты отражения в этих состояниях.

E1  ^0.20 Вычислите $\Delta \Gamma$ для SET, подключенного к линии с импедансом $50\ \Omega$ (рис. 6).

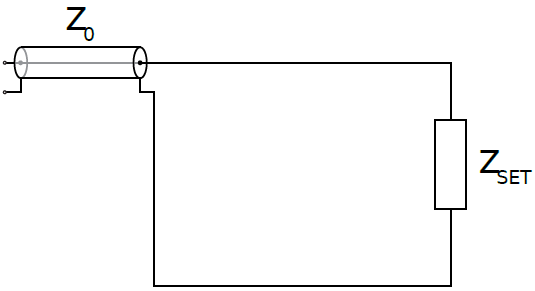
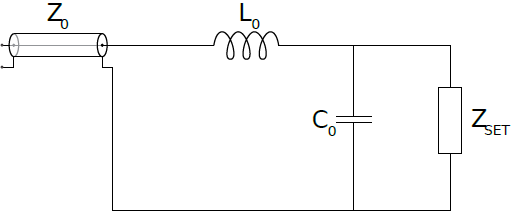
Для увеличения $\Delta \Gamma$ (и, соответственно, чувствительности рефлектометрии) в цепь включают индуктивность (рис. 7). Учтите, кроме того, технологически неизбежную внутреннюю емкость $C_0\approx0.4\: \textrm{пФ}$. Рефлектометрия проводится сигналом угловой частоты $\omega_\text{rf}$.

E2  ^0.80 Найдите условие на $L_0$, необходимое для того, чтобы $\Delta \Gamma$ было порядка единицы. Для случая $\omega_{\text{rf}}/(2\pi)=100\: \textrm{МГц}$ вычислите $L_0$ и соответствующее ей $\Delta \Gamma$.

Часть F. Регистрация заряда с помощью квантовой точки с одним электродом (1.5 балла)

В практических применениях количество электродов, подходящих к квантовым точкам, стремятся уменьшить. В квантовых точках с одним электродом (Single Lead Quantum Dot, SLQD) отсутствуют электроды S и G, а через затвор G осуществляется и управление состоянием QD, и рефлектометрия.

SLQD в OFF-состоянии является изолятором, как и SET. Однако, в отличие от SET, SLQD в ON-состоянии эквивалентен конденсатору емкости $C_\text{q}$. Для максимизации $\Delta\Gamma$ собирают изображенную на рисунке 8 схему. Емкость $C_0\approx0.4\: \textrm{пФ}$ конструктивно неизбежна и фиксирована, а индуктивность $L_0$ и частота сигнала $\omega_\text{rf}$ могут быть выбраны такими, чтобы оптимизировать измерения. Импеданс линии $Z_0=50 \, \Omega$.

F1  ^1.00 Предложите, как выбрать $\omega_\text{rf}$ и $Z_\text{C}=\sqrt{L_0/C_0}$, чтобы получить $\Delta\Gamma \sim 1$ при фиксированных $C_0$ и $C_q$. В ответ запишите формулы для нахождения $\omega_\text{rf}$ и $Z_{\text{C}}$.

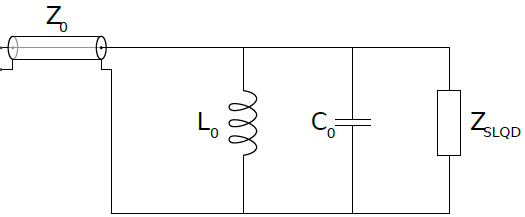
Подбираемые оптимальные значения индуктивности $L_0$ довольно велики и не всегда реализуемы. Поэтому для увеличения чувствительности рефлектометрии иногда требуется использовать элементы другого типа.

F2  ^0.50 Ставится цель получить $\Delta \Gamma \sim 1$, не прибегая к использованию значительных $L_0$. Считая $L_0$ (и, таким образом, $Z_C$) фиксированной, нарисуйте схему, задействующую еще один элемент при подключении линии к SLQD. Найдите выражение для номинала этого элемента.