
Рассмотрим простейший процесс рассеяния: частица 1 (налетающая частица) с кинетической энергией $K_1$ летит из бесконечности и упруго сталкивается с покоящейся частицей 2 (частицей-мишенью), в результате чего кинетическая энергия и направление движения первой частицы меняются.
Пусть кинетическая энергия частицы 1 после рассеяния равна $K'_1$. Введём кинематический фактор $k\equiv\frac{K'_1}{K_1}$.
Обозначим как $\theta$ угол между направлениями движения частицы до и после рассеяния. Введём также величину $R$ — отношение массы второй частицы к массе первой. Зафиксируем некоторое значение $R$ и посмотрим на поведение $k$ как функции $\theta$.
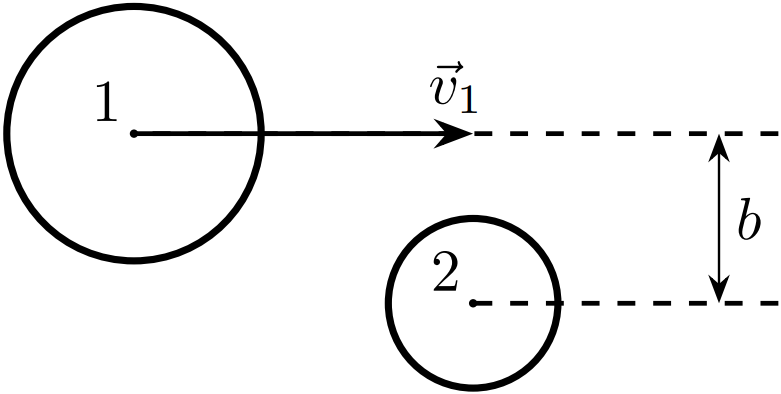
Пусть теперь массы покоя обеих частиц равны $m_0$, размеры частиц несущественны, а скорость налетающей частицы настолько велика, что возникает необходимость учёта релятивистских эффектов. Скорость света в вакууме равна $c$.