Если луч лазера сфокусировать на группе нейтральных атомов, то их можно «захватить» и охладить до практически нулевой абсолютной температуры. При околонулевых температурах можно получить особое состояние вещества, называемое бозе-конденсатом.

Нейтральный атом натрия можно представить в виде ядра с положительным зарядом $e$, которое окружено однородным электронным облаком с отрицательным зарядом $-e$. Масса облака пренебрежимо мала по сравнению с массой ядра. В отсутствие внешнего электрического поля центры электронного облака и ядра совпадают.

Если атом поместить в электрическое поле, он поляризуется, т.е. у атома появляется дипольный момент. Этот диполь взаимодействует с тем же электрическим полем. Поле определяется распределением интенсивности $I(\vec{r})$ в лазерном пучке и частотой. Если специально подобрать частоту и интенсивность, можно создать потенциальную яму, размерами которой будут ограничены атомы.

Атом, помещенный в однородное электрическое поле $\vec{E_0}=E_0 \hat{u}$ ($\hat{u}$ — единичный вектор), приобретает дипольный момент $\vec{p_0}=el\hat{u}=\alpha E_0 \hat{u}$ ($\alpha$ — поляризуемость).

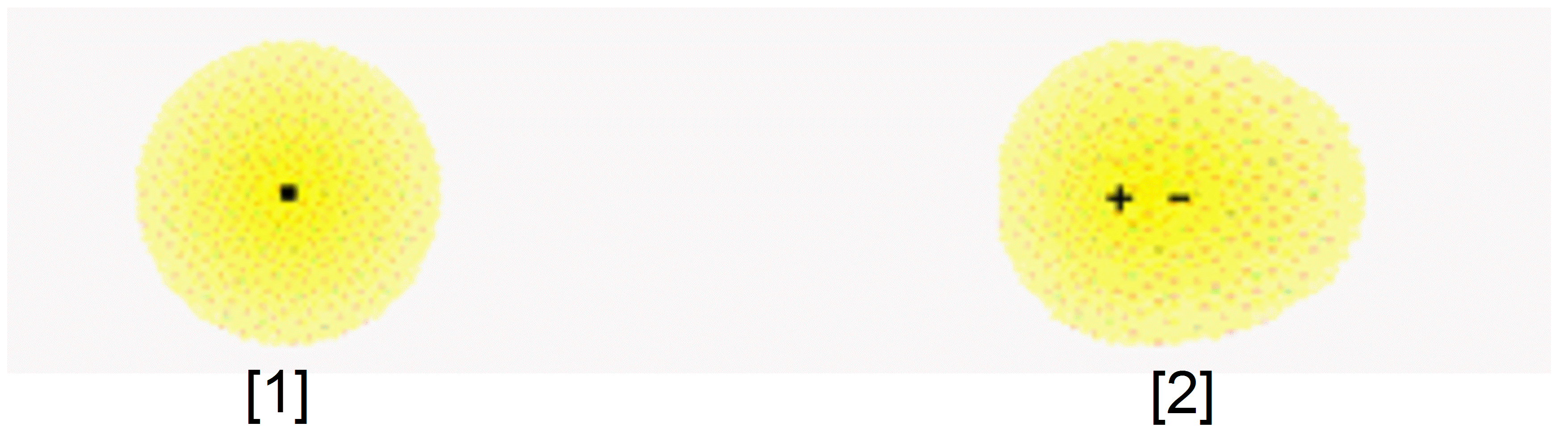
Пусть в начальный момент времени поле выключено. Затем напряженность поля очень медленно повышают до $E_0$. В произвольный момент времени напряженность поля $\vec{E}=E\hat{u}$.

A1  ^0.75 Найдите в этом случае мгновенную поглощаемую атомом мощность. Ответ выразите через векторы $\vec{E}$ и $\dot{\vec{p}}$ ($\dot{\vec{p}}$ — скорость изменения дипольного момента).

A2  ^0.75 Найдите полную работу, совершенную полем к моменту, когда его напряженность достигла $E_0$, и отсюда получите выражение для потенциальной энергии диполя $U_{induced}$ через векторы $\vec{E_0}$ и $\vec{p_0}$.

Если поле выключить, то электронное облако в атоме колеблется с собственной частотой $\omega_0$.

Рассмотрим атом в переменном электрическом поле $\vec{E}(\vec{r},t) =\hat{u}\ E_0(\vec{r})\cos\omega t$ . Индуцированный дипольный момент $\vec{p}$ будет осциллировать с той же частотой $\omega$. Колеблющийся диполь, как известно, излучает. Это приводит к тому, что дипольный момент и внешнее поле сдвинуты по фазе: $\vec{p}(\vec{r},t)=\hat{u}\ E_0(\vec{r})\alpha(\omega)\cos[\omega t+\varphi(\omega)]$, причем и поляризуемость $\alpha$, и сдвиг фаз $\varphi$ зависят от частоты $\omega$. Т.к. эти процессы происходят с высокой частотой, мы можем наблюдать и измерять лишь усредненные по периоду $2\pi/\omega$ величи́ны.

По определению усреденение некой величины по периоду значит $\left\langle {f\left( t \right)} \right\rangle = \cfrac{\omega }{{2\pi }}\int\limits_0^{2\pi /\omega } {f\left( t \right)dt} $. Здесь и далее запись $\langle ... \rangle$ означает усреднение величины в скобках по времени.

Интенсивность $I(\vec{r})$ лазерного пучка связана с амплитудой $E_0$ электрического поля следующим образом: $I(\vec{r})=\cfrac{\varepsilon_0c\ E_0^2(\vec{r})}{2}$ , где $\varepsilon_0$ — электрическая постоянная и $c$ — скорость света.

B1  ^1.00 Найдите потенциальную энергию диполя ${U_{dip}}\left( {\vec r} \right) = \left\langle {{U_{induced}}\left( {\vec r,t} \right)} \right\rangle $.

Ответ выразите через $\alpha,\:\varphi,\:\varepsilon_0,\:c$ и $I(\vec{r})$.

Когда атомы находятся в лазерном пучке, на них рассеиваются фотоны. Это можно описать поглощением и испусканием света. Эти процессы характеризуются скоростью рассеяния $\Gamma_{sc}(\overrightarrow{r})=\dfrac{\langle P_{abs}(\overrightarrow{r})\rangle}{\hslash\omega} $. Где $\langle P_{abs}(\overrightarrow{r})\rangle$ — усредненная по времени мощность, поглощаемая из лазерного пучка, а $\hbar\omega$ — энергия фотона $(\hbar=h/2\pi)$.

C1  ^1.00 Выразите $\Gamma_{sc}(\vec{r})$ через $\alpha,\:\varphi,\:\varepsilon_0,\:c,\:I(\vec{r}),\ \hslash$ и $\omega$.

Обе величины $U_{dip}$ и $\Gamma_{sc}(\vec{r})$ зависят от поляризуемости $\alpha$. Чтобы ее рассчитать, рассмотрим одномерный осциллятор в поле $\vec{E}(t)=\hat{u}\ E_0\cos\omega t$. Ось $Ox$ параллельна единичному вектору $\hat{u}$. Координатой $x$ обозначим смещение электронного облака, полагая ядро неподвижным. В уравнение колебаний входят три слагаемых.

$\bullet$ $-m_e\omega_0^2x\cdot\hat{u}$ — возвращающая сила, соответствующая свободным колебаниям с собственной частотой $\omega_0$,

$\bullet$ $-eE_0 \cos\omega t\cdot\hat{u}$ — вынуждающая сила, $$

$\bullet$ $-m_{e}\gamma_{\omega}\dot{x} \cdot \hat{u}$ — затухание, связанное с излучением. Оно характеризуется коэффициентом затухания $\gamma_{\omega}$, зависящим от частоты.

Итак, уравнение колебаний выглядит следующим образом: $\ddot x + {\gamma_\omega }\dot x + \omega _0^2x = \cfrac{{ - eE_0 \cos \omega t}}{{{m_e}}}$, и его решение может быть найдено в виде $x=x_0\cos(\omega t+\varphi)$. Здесь $x_0$ и $\varphi$ нужно определять.

D1  ^2.00 Выразите поляризуемость $\alpha$ через $\gamma_{\omega},\:e,\:m_e,\:\omega_0$ и $\omega$.

Рассмотрим еще одну упрощенную модель, в которой в отсутствие внешнего поля центр электронного облака движется по круговой орбите с частотой $\omega$ и скоростью $v$. Когда электрон движется с ускорением, мощность излучения задается формулой ${P_L} = \cfrac{1}{{6\pi {\varepsilon _0}}}\cfrac{{{e^2}{a^2}}}{{{c^3}}}$, $a$ — ускорение. Силу, соответствующую затуханию, можно записать как ${F_d} = - {m_e}{\gamma _\omega }v$. Считайте, что энергия, теряемая электроном за один оборот, много меньше его полной энергии.

E1  ^1.00 Выразите коэффициент затухания $\gamma_{\omega}$ через $e,\ \varepsilon_0,\ c,\ m_e$ и $\omega$.

Когда частота вынуждающей силы $\omega$ близка к собственной частоте осциллятора $\omega_0,$ поляризуемость возрастает. Это приводит как к росту потенциальной энергии диполя, так и к увеличению скорости рассеяния. В экспериментах стараются снизить рассеяние, аглубину потенциальной ямы поддержать на достаточном уровне. Для оптимизации этого удобно использовать величину ${{U_{dip}}\left( {\vec r} \right)}/{\hbar {\Gamma _{sc}}\left( {\vec r} \right)}$.

F1  ^0.50 Определим при $\omega=\omega_0$ коэффициент затухания $\gamma \equiv {\gamma _{{\omega _0}}}$.

Выразите ${{U_{dip}}\left( {\vec r} \right)}/{\hbar {\Gamma _{sc}}\left( {\vec r} \right)}$ через $\omega,\ \omega_0$ и $\gamma$.

В предыдущем пункте было получено, что ${\Gamma _{sc}}\left( {\vec r} \right)$ — величина положительная, а при $\omega<\omega_0$ отношение ${{U_{dip}}\left( {\vec r} \right)}/{\hbar {\Gamma _{sc}}\left( {\vec r} \right)}$ отрицательно. Это означает, что потенциальная энергия отрицательна, и атомы удерживаются в той области пучка, где интенсивность максимальна (в оптической ловушке). Если начать уменьшать глубину потенциальной ямы, то высокоэнергетичные атомы покинут область. Это значит, что удерживаемый газ атомов можно охладить до сверхнизких температур и получить бозе-конденсат.

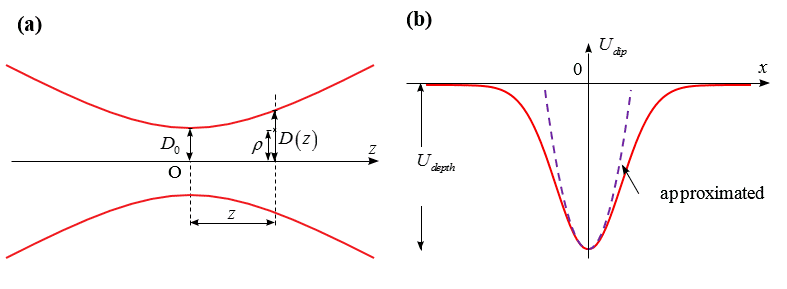
Рассмотрим известный эксперимент с разреженным газом атомов натрия, которые могут образовывать бозе-конденсат. Атомы удерживаются оптической ловушкой. Лазер излучает на длине волны $\lambda$, которой соответствует $\omega < \omega_0$. Распределение интенсивности в пучке задается гауссовой функцией $I\left( {\rho ,z} \right) = \cfrac{{2P}}{{\pi D^2{{\left( z \right)}}}}\ \exp \left( { - \cfrac{{2{\rho ^2}}}{{D^2{{\left( z \right)}}}}} \right)$, где $\rho = \sqrt {{x^2} + {y^2}} $, а ширина пучка $D\left( z \right) = {D_0}\sqrt {1 + {z^2}/z_R^2} $ и ${z_R} = \pi D_0^2/\lambda $ (рис. 2а). Полная мощность излучения $P$ и минимальная ширина пучка $D_0$ определяют параметры потенциальной ямы (оптической ловушки). Один из них — ее глубина $U_{depth}$, которая определяется как абсолютное значение потенциальной энергии в ее локальном минимуме (рис. 2b). На бесконечности потенциальную энергию принимают нулевой.

G1  ^0.50 Выразите глубину потенциальной ямы $U_{depth}$ через $c,\ \omega,\ \omega_0,\ \gamma,\ P$ и $D_0$.

G2  ^1.00 Пусть мощность лазера $P=4$ мВт, длина волны излучения $\lambda=985$ нм, $D_0=6$ мкм, длина волны D-линии натрия $\lambda_0=589$ нм. Получите выражение, а также численно рассчитайте глубину потенциальной ямы $U_{depth}$. Ответ приведите в Кельвинах эквивалентной температуры $T_0$, при которой тепловая энергия атомов равна глубине потенциальной ямы.

При температуре электронного облака $T$, много меньшей, чем определенная выше температура $T_0$, потенциальную энергию у дна ямы можно приближенно считать гармонической $U_{dip}(\rho,z)=- U_{depth}+\cfrac{1}{2}\ m\ \Omega_{\rho}^2\rho^2+\cfrac{1}{2}\ m\ \Omega_z^2z^2$, где $m$ — масса атома натрия, а $\Omega_{\rho},\:\Omega_z$ — частоты колебаний в соответствующих направлениях.

H1  ^0.50 Выразите $\Omega_{\rho}$ и $\Omega_z$ через $T_0,\:m,\:D_0,\:z_R$ и постоянную Больцмана $k_B$.

При низких тепературах газ атомов натрия состоит из атомов бозе-конденсата и тепловых атомов. Атомы бозе-конденсата подчиняются соотношению неопределенностей, таким образом можно оценить размер области, занимаемой газом, и распреление скоростей в ней. С другой стороны, тепловые атомы описываются уравнениями классической физики и подчиняются распределению Максвелла-Больцмана.

Среднее расстояние от атомов натрия до центра ловушки — это характерный размер области, занимаемой газом. Потенциальная энергия монотонно возрастает с ростом размера области, атом пытается ее уменьшить, стараясь занять уровень с минимальной энергией. С другой стороны, по мере уменьшения размера области, соотношение неопределенностей приводит к увеличению скорости атомов, т.е. к увеличению кинетической энергии. Поэтому существует некий оптимальный размер этой области, когда описанные эффекты скомпенсированы.

Рассмотрим одномерную потенциальную яму $U(z)=\mathrm{const}+\cfrac{1}{2}\ m\Omega_z^2z^2$.

I1  ^0.50 Оцените размер области $z_0$, занимаемой газом в состоянии бозе-конденсата. Ответ выразите через $m,\:\hbar$, $\Omega_z$.

I2  ^0.25 Выразите энергию $E_{\mathrm{min}}$ низшего энергетического уровня через $\hbar$ и $\Omega_z$.

I3  ^0.25 Выразите среднюю скорость $v_0$ атомов через $m,\:\hbar$, $\Omega_z$.

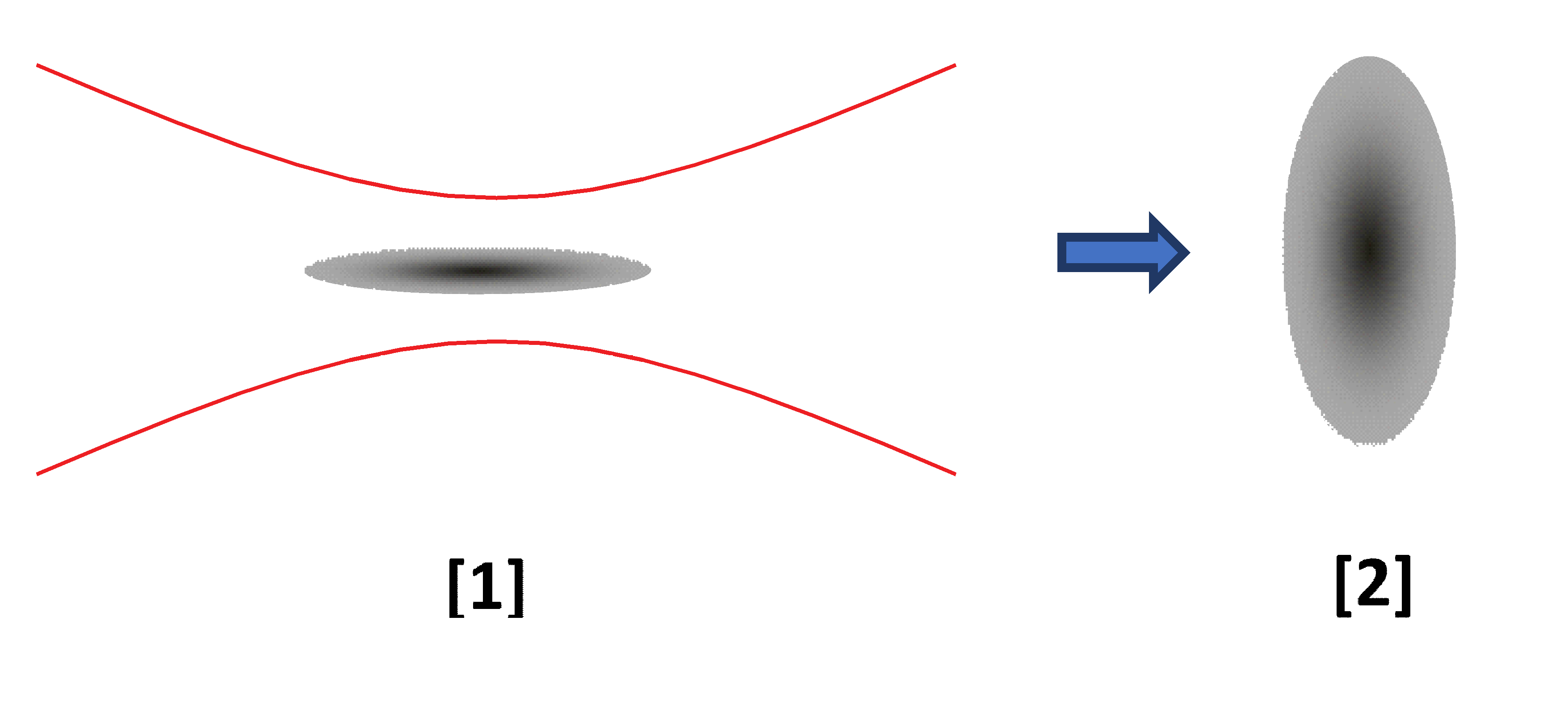
Рассмотрим, как будут вести себя атомы газа из бозе-конденсата и тепловые атомы, если отключить ловушку. Распределение скоростей тепловых атомов — максвелловское, даже если ловушка анизотропна. Напротив, распределение скоростей в бозе-консате анизотропно. А именно, бозе-конденсат расширяется быстрее вдоль осей, где он удерживался сильнее, по сравнению со скоростью расширения вдоль оси, где он удерживался слабо. Если представить, что удерживаемый бозе-конденсат имел сигарооразную форму, то после отключения ловушки он примет форму, более похожую на блинчик.

J1  ^0.50 Выразите отношение ${z_0}/{\rho_0}$ через $\Omega_{\rho}$ и $\Omega_z$, где $z_0$ и $\rho_0$ — начальные размеры области, занимаемой бозе-конденсатом.

J2  ^0.50 Если выключить ловушку, то бозе-конденсат будет разлетаться с различными скоростями $v_{\rho}$ и $v_z$ в разных направлениях. Выразите отношение ${v_{\rho}}/{v_z}$ через $\Omega_{\rho}$ и $\Omega_z$.

J3  ^0.50 Найдите отношение ${z_L}/{\rho_L}$ размеров области расширяющегося бозе-конденсата, когда они намного больше первоначальных (${z_L} \gg {z_0}$ и ${\rho _L} \gg {\rho _0}$). Скорости расширения бозе-конденсата считайте неизменными.

J4  ^0.50 Найдите отношение ${{{z_{T,L}}}}/{{{\rho _{T,L}}}}$ размеров области расширяющегося газа тепловых атомов, когда размеры намного больше первоначальных (${z_{T,L}} \gg {z_0}$ и ${\rho _{T,L}} \gg {\rho _0}$).