Полезный факт:

${e^x} = 1 + \frac{x}{{1!}} + \frac{{{x^2}}}{{2!}} + \frac{{{x^3}}}{{3!}} + ...$

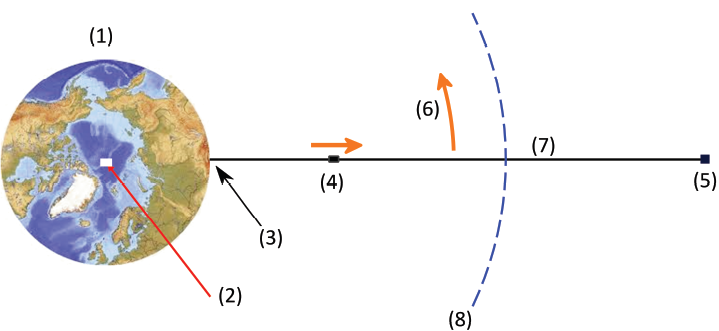
Ракеты — не самый эффективный способ вывода грузов на орбиту. Космический лифт, если его построить, будет гораздо более эффективной технологией (рис. 1). Основой элемент космического лифта — трос, один конец которого закреплен на поверхности Земли, на экваторе, а другой конец расположен на высоте, большей, чем высота геостационарной орбиты. Геостационарная орбита имеет радиус примерно 42300 км и период обращения такой же, как собственное вращение Земли. Для реализации идеи космического лифта потребуются материалы намного прочнее и легче, чем сталь. Одним из таких материалов могут стать углеродные нанотрубки. В этой задаче мы рассмотрим две конструкции космического лифта, механические свойства углеродных нанотрубок, а также некоторые применения лифта.

Масса Земли $M=5.98\times10^{24}\text{ }$ кг, радиус Земли $R\:=\:6370$ км, радиус геостационарной орбиты $R_G=42300$ км, масса Солнца $M_S=2\times10^{30}$ кг, радиус орбиты Земли $R_E\:=\:1.5\times10^8 = 1$ а.е. (а.е. – астрономическая единица), скорость орбитального движения Земли $30.9$ км/с, угловая скорость вращения Земли вокруг своей оси $\omega=7.27\times10^{-5}$ рад/с.

Космический лифт с цилиндрическим тросом постоянного сечения

В этой части рассматривается конструкция лифта с цилиндрическим тросом постоянного сечения площадью $A$. Плотность материала троса $\rho$. Трос представляет собой вертикальный цилиндр на экваторе Земли. Высота цилиндра больше, чем высота геостационарной орбиты. Длина троса такая, что механическое напряжение троса в точке на поверхности Земли равно нулю. Механическое напряжение — сила натяжения на единицу площади поперечного сечения. Трос находится в натяжении по всей своей длине. Механические напряжения троса такие, что каждый элемент троса находится в равновесии под действием сил натяжения, гравитационных сил и центробежных.

A1  ^0.50 Вычислите высоту верхнего конца троса над поверхностью Земли $L$.

A2  ^0.50 Найдите расстояние $r$ между центром Земли и точкой, в которой механическое напряжение троса максимально.

A3  ^0.50 Выразите максимальное механическое напряжение троса $\sigma_{max}$ через $\rho,\:R_G,\:R$ и ускорение свободного падения $g$. Вычислите отношение максимального механического напряжения троса $\sigma_{max}$ к пределу прочности стали $\sigma_{steel}$. Считайте, что трос изготовлен из стали плотностью $7900$ кг/м$^3$ с пределом прочности $5.0$ ГПа.

Углеродные нанотрубки

Вычисления прошлой части показывают, что для реализации проекта необходим очень легкий, но прочный материал. Материал из углеродных нанотрубок удовлетворяет этим требованиям из-за наличия прочных химических связей между относительно легкими атомами.

В природе существует две аллотропных модификации углерода: алмаз и графит. В алмазе каждый атом углерода окружен четырьмя ближайшими соседними атомами, которые являются вершинами тетраэдра. Графит имеет слоистую структуру. В каждом слое атомы углерода выстроены в шестиугольную плоскую структуру. Каждый атом в этой плоскости имеет трёх ближайших соседей. Ковалентные связи между такими атомами в слое графита оказываются даже прочнее, чем связи между атомами в алмазе. Мягкость графита объясняется слабыми Ван-дер-Ваальсовыми силами между атомами разных слоёв.

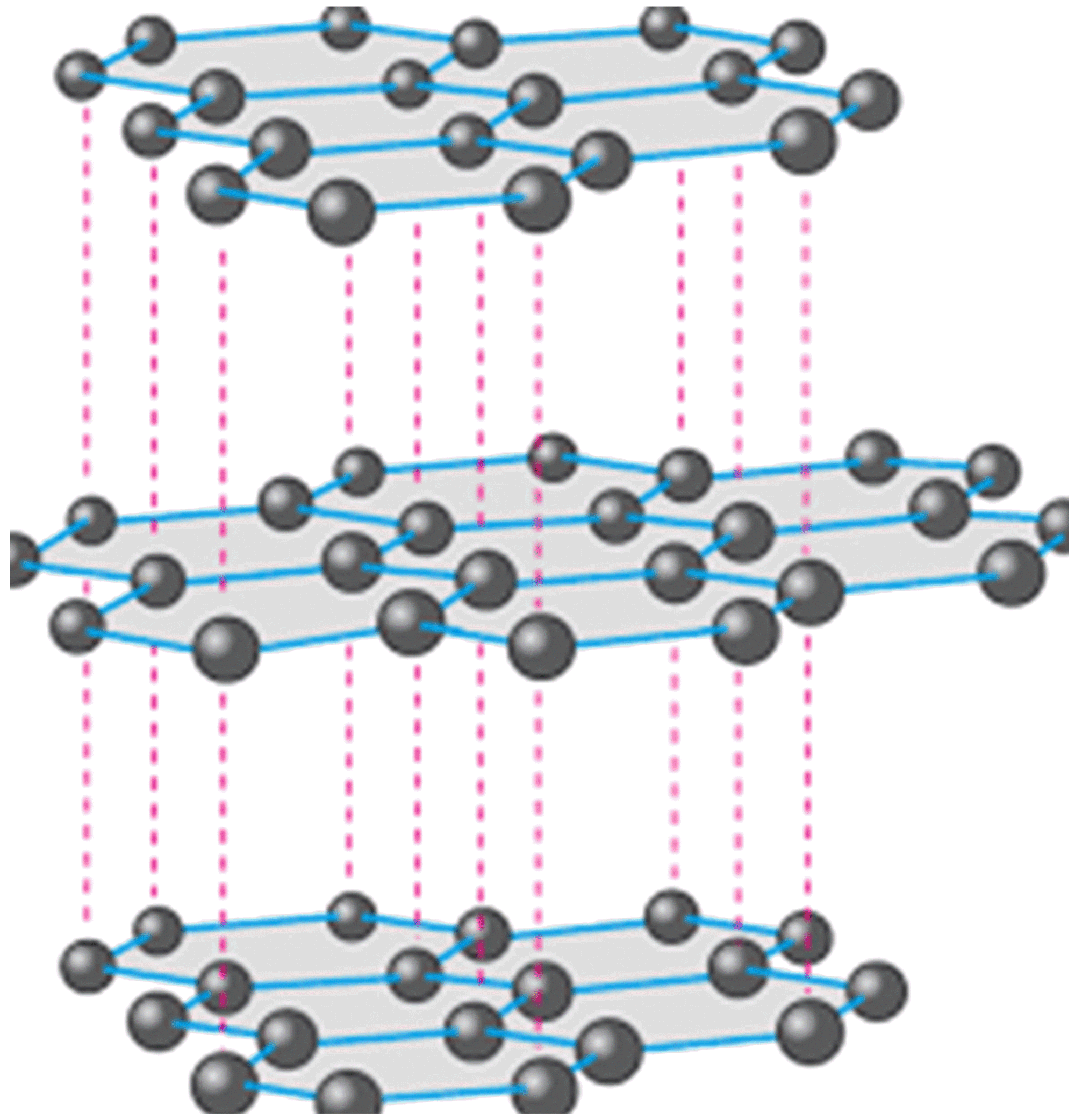
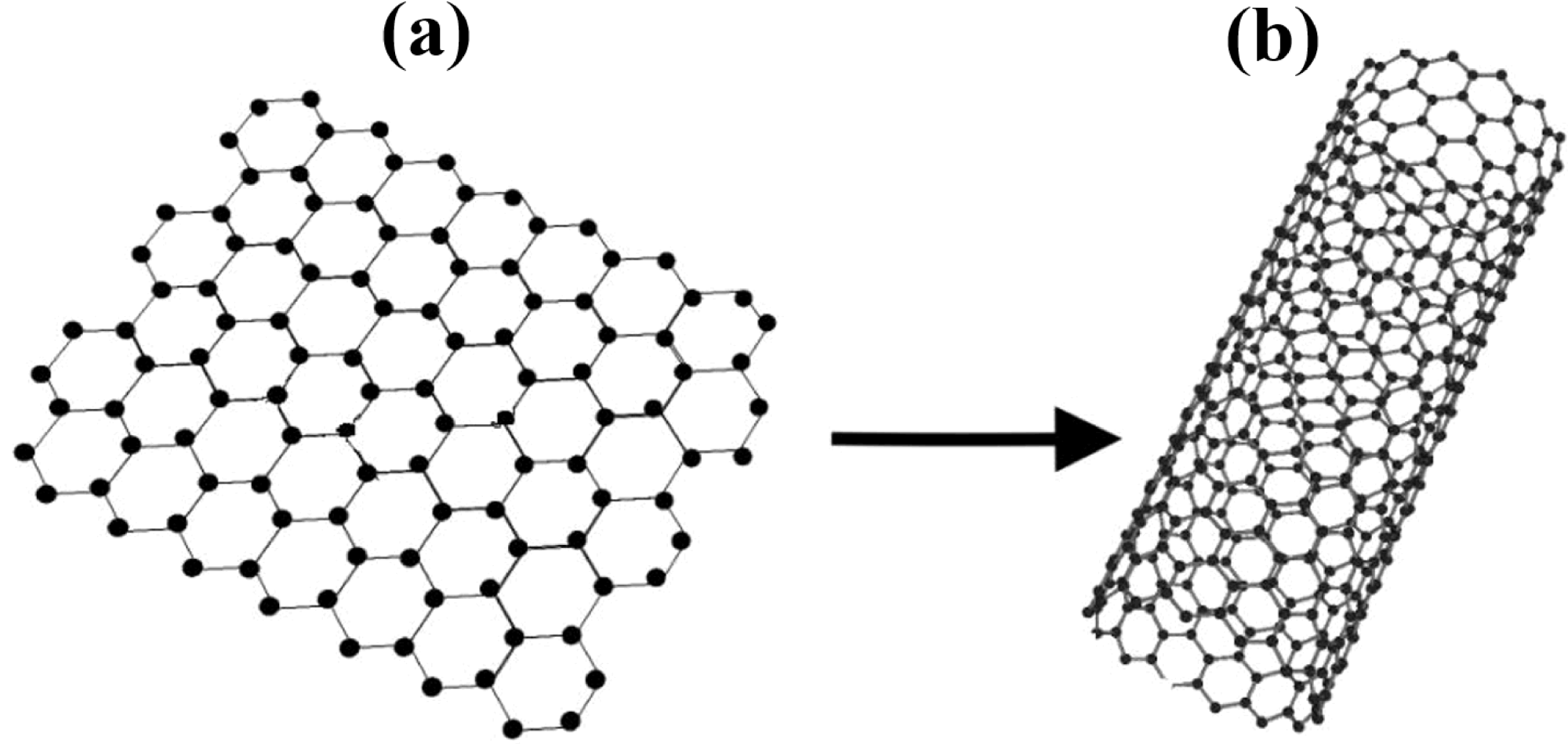
Одноатомный слой графита называется графеном (рис. 3а). Отдельный лист графена нестабилен и склонен сворачиваться в сферы или нанотрубки (рис. 3b).

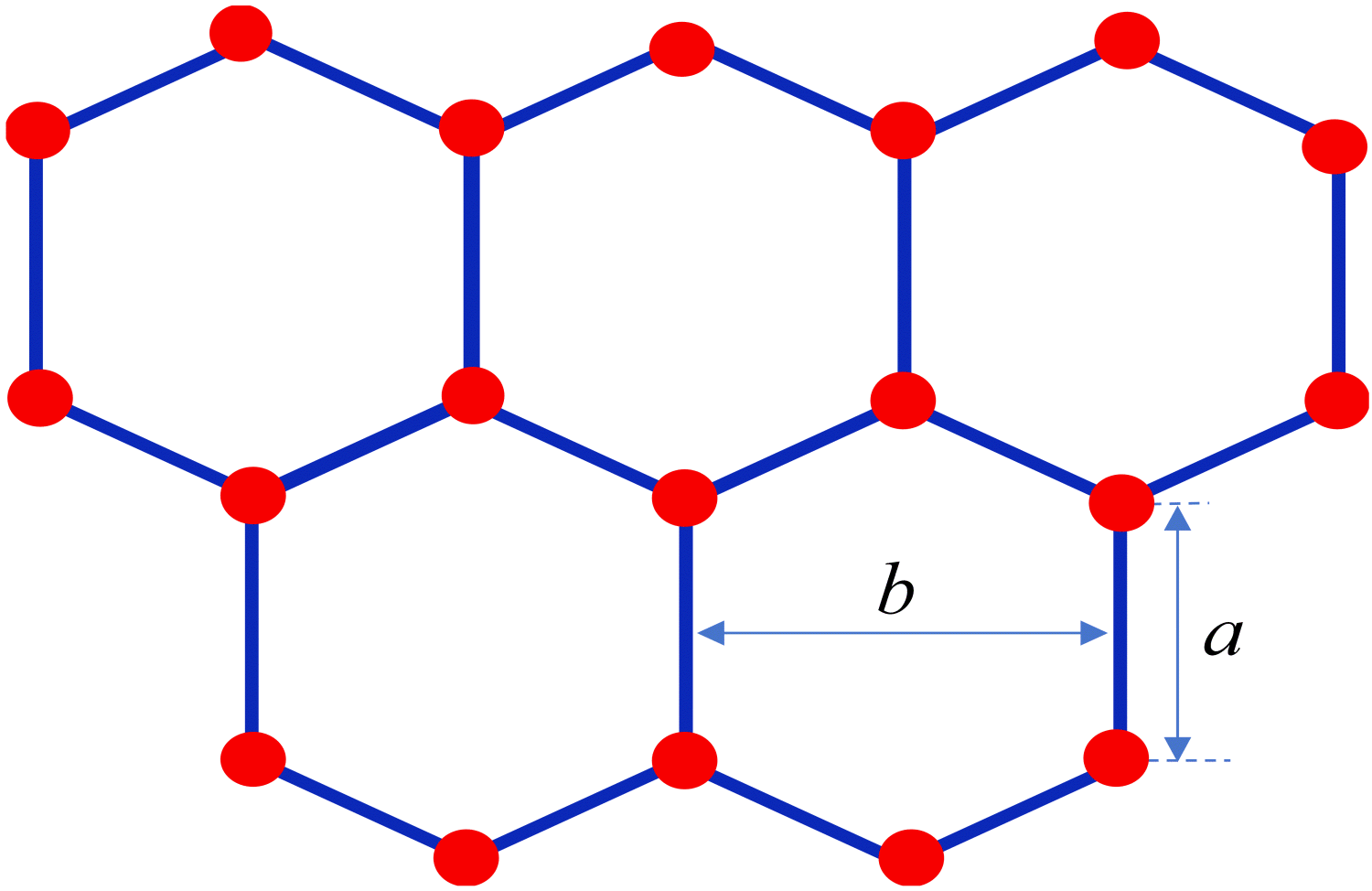
Шестиугольная кристаллическая решетка графена изображена на рис. 4. Расстояние между двумя соседними атомами углерода $a=0.142$ нм. Расстояние между двумя ближайшими параллельными связями равно $b=0.246$ нм. Из-за очень сильных ковалентных связей углеродные нанотрубки обладают чрезвычайно большим модулем Юнга, большим пределом прочности и очень маленькой плотностью. Модуль Юнга есть отношение механического напряжения к относительному удлинению.

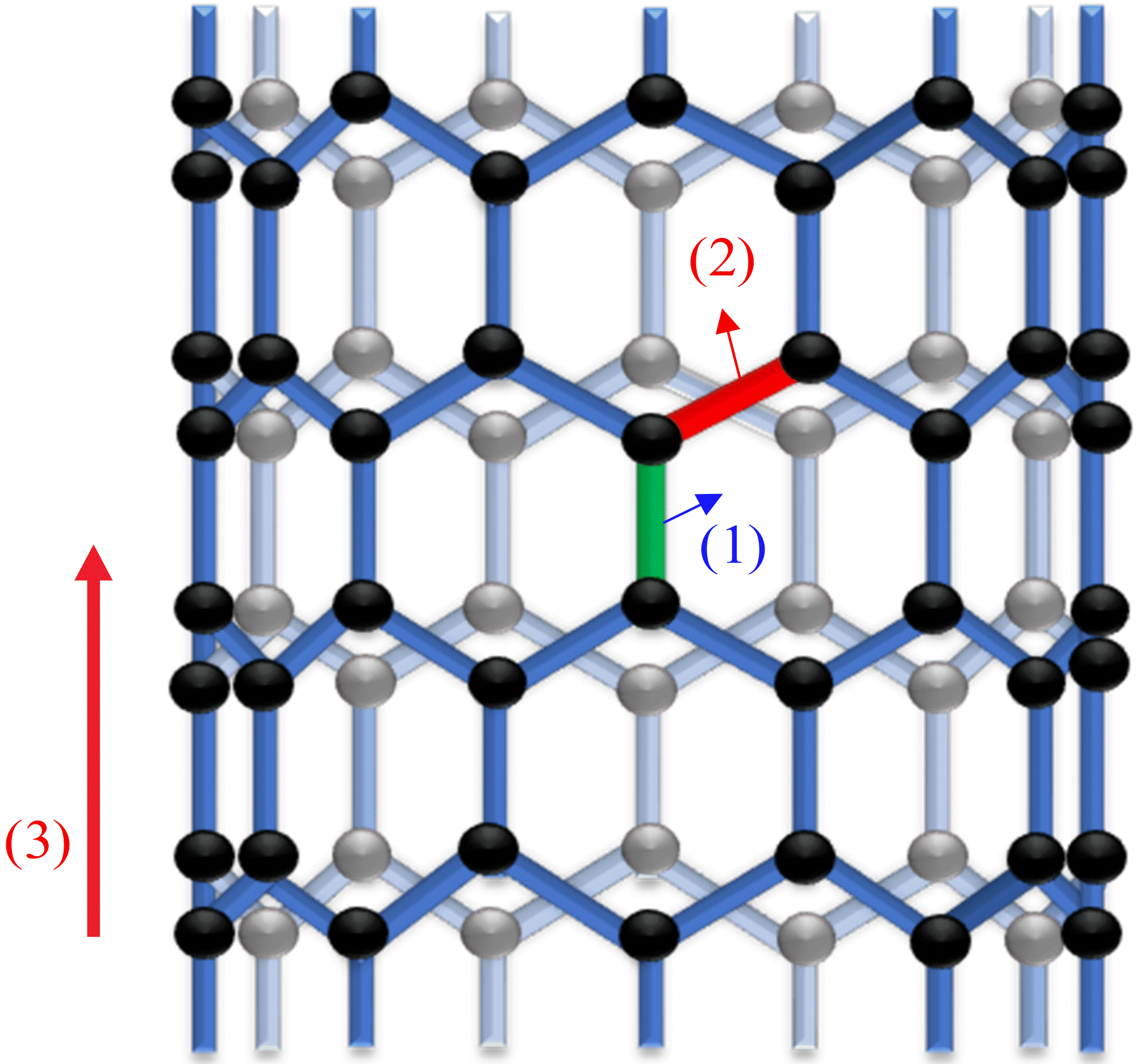
Далее мы вычислим механические свойства углеродной нанотрубки, которая имеет 27 углерод-углеродных параллельных связей вдоль своей оси (рис. 5).

Энергия связи между двумя атомами углерода описывается потенциалом Морзе $V(x)=V_0(e^{-4\frac{x}{a}}-2e^{-2\frac{x}{a}})$. Здесь $a=0.142$ нм — расстояние между двумя соседними атомами углерода в равновесии, $V_0=4.93$ эВ — энергия связи, $x$ — смещение атомов от положения равновесия. Далее мы аппроксимируем потенциал Морзе в виде квадратичного потенциала $V(x) = P + Qx^2$. Взаимодействуют только соседние атомы. В данном приближении можно считать, что атомы скрепляются «пружинками» с некоторой жесткостью $k$. Изменения углов между связями пренебрежимо малы и не рассматриваются.

B1  ^0.25 Выразите коэффициенты $P$ и $Q$ через $a$ и $V_0$.

B2  ^0.25 Вычислите характерную жесткость «пружинки» $k$.

B3  ^0.50 Вычислите модуль Юнга углеродной нанотрубки $E$.

При максимально возможном удлинении «пружинки» $x_{\max}$ её потенциальная энергия равна энергии связи. Это позволяет оценить предел прочности углеродной нанотрубки.

B4  ^0.50 Вычислите максимальное удлинение $x_{\max}$ «пружинки».

B5  ^0.50 Оцените предел прочности $\sigma_0$ углеродной нанотрубки.

B6  ^0.50 Оцените плотность углеродной нанотрубки $\rho$. Молярная масса углерода 12 г/моль.

Космический лифт с коническим тросом постоянного механического напряжения

В данной части мы рассматриваем трос космического лифта с переменной площадью сечения, но с постоянным механическим напряжением $\sigma$ и постоянной плотностью $\rho$ по всей длине. Трос имеет осевую симметрию и расположен вертикально на экваторе. Высота троса больше, чем высота геостационарной орбиты. Обозначим площадь поперечного сечения троса на поверхности Земли как $A_S$, на высоте геостационарной орбиты как $A_G$.

C1  ^0.50 Найдите зависимость площади поперечного троса $A(h)$ от высоты $h$. Высота $h$ отсчитывается от поверхности Земли.

C2  ^0.50 Трос устроен так, что площади поперечного сечения его концов равны. Найдите расстояние $H$ от центра Земли до верхнего конца троса.

C3  ^0.50 Найдите отношение $A_G/A_S$, если трос изготовлен из углеродных нанотрубок с пределом прочности 130 ГПа и плотностью $1300$ кг/м$^3$.

C4  ^1.00 Можно значительно сократить длину троса, если его часть сверху убрать и прикрепить противовес соответсвующей массы. Пусть $h_C$ — высота троса, отсчитываемая от геостационарной орбиты до противовеса. Найдите массу противовеса $m_C$.

Применение: вывод нагрузки на орбиту и запуск космических кораблей к другим планетам

Основная идея применения космического лифта — выводить с помощью него полезную нагрузку на орбиту и запускать космические корабли к другим планетам. Способ запуска объектов довольно прост: объект поднимается на высоту $r$ и отпускается без начальной скорости. Считайте, что движение троса происходит в плоскости орбиты Земли.

D1  ^0.50 Если с некоторой точки троса отпустить объект, то он сможет покинуть гравитационное поле Земли. Найдите критический радиус $r_C$, измеряемый от центра Земли, для которого это произойдет.

Использование троса высотой больше $r_C$ необходимо, если мы хотим запускать объекты к другим планетам. Пусть конец троса находится на расстоянии 107000 км от центра Земли.

D2  ^1.00 Найдите, каких минимального $r_{min}$ и максимального $r_{max}$ расстояний от Солнца может достичь объект, отпущенный с конца троса. Выразите ваш ответ в астрономических единицах (а.е.). Притяжением Земли на такой высоте можно принебречь.