В этой задаче мы рассмотрим три основных термоэлектрических эффекта: закон Джоуля-Ленца, эффекты Зеебека и Пельтье.

Закон Джоуля-Ленца. При направленном движении носителей заряда они передают часть энергии в колебательное движение кристаллической решетки, поэтому кристалл нагревается. Этот процесс — необратимый.

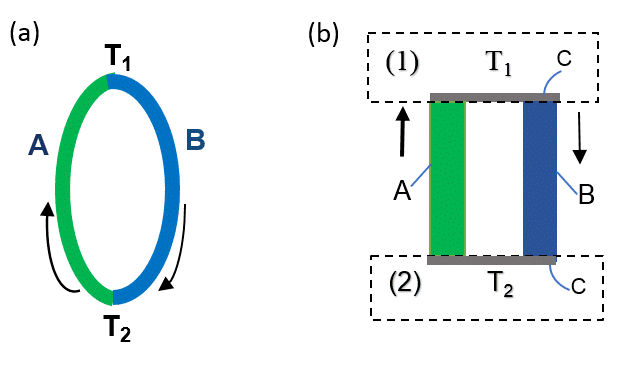
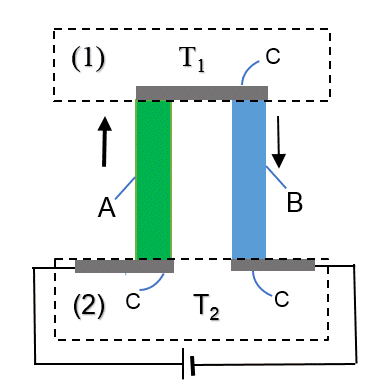
Эффект Зеебека наблюдается в термопаре, состоящей из двух разных проводников $A$ и $B$, спаянных друг с другом (рис. 1а) либо соединенных через промежуточный материал $C$ (рис. 1b). Когда спаи термопары поддерживаются при разных температурах $T_1$ и $T_2$ (рис. 1), в системе возникает ЭДС

$$\epsilon=\alpha(T_1-T_2)$$

где $\alpha$ — коэффициент Зеебека термопары и считается, что он не зависит от температуры.

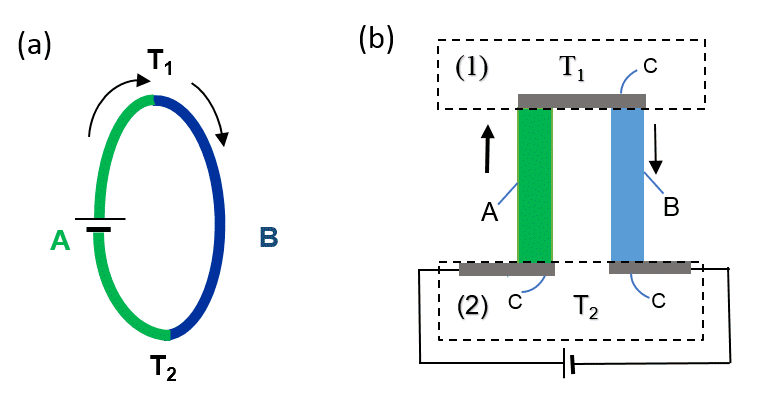
Эффект Пельтье. Если через термопару пропустить ток, то, в зависимости от направления, куда он течет, на спае может выделяться или поглощаться тепло. Соединение проводников термопары может быть как прямым (рис. 2а), так и через промежуточный материал (рис. 2b). Выделяемая (или поглощаемая) на спаях мощность $q$ записывается следующим образом:

$$q=\pi I$$

где $\pi$ — коэффициент Пельтье. Эффекты Зеебека и Пельтье — обратимые. Цепь, показанная на рисунке 2b, может использоваться как холодильник, причем тепло отбирается у одного из спаев и выделяется на другом. Излучением, конвекцией и теплопроводностью можно пренебречь. Вся теплопередача происходит внутри тепловых резервуаров и термопары.

Для численных расчетов в Таблицах 1 и 2 приведены значения тепловых и электрических характеристик материалов.

Часть I. Теплопроводность и термоэлектрический генератор (7.5 баллов)

Теплопроводность в однородном проводнике

Вдоль однородного проводника течет ток силой $I$ (рис. 3). Удельное сопротивление материала $\rho$, коэффициент теплопроводности $k$. Координаты концов проводника: $x=0$ и $x=L$. Температуры концов проводника поддерживаются постоянными и равными $T_1$ при $x=0$ и $T_2$ при $x=L$ ($T_1>T_2$).

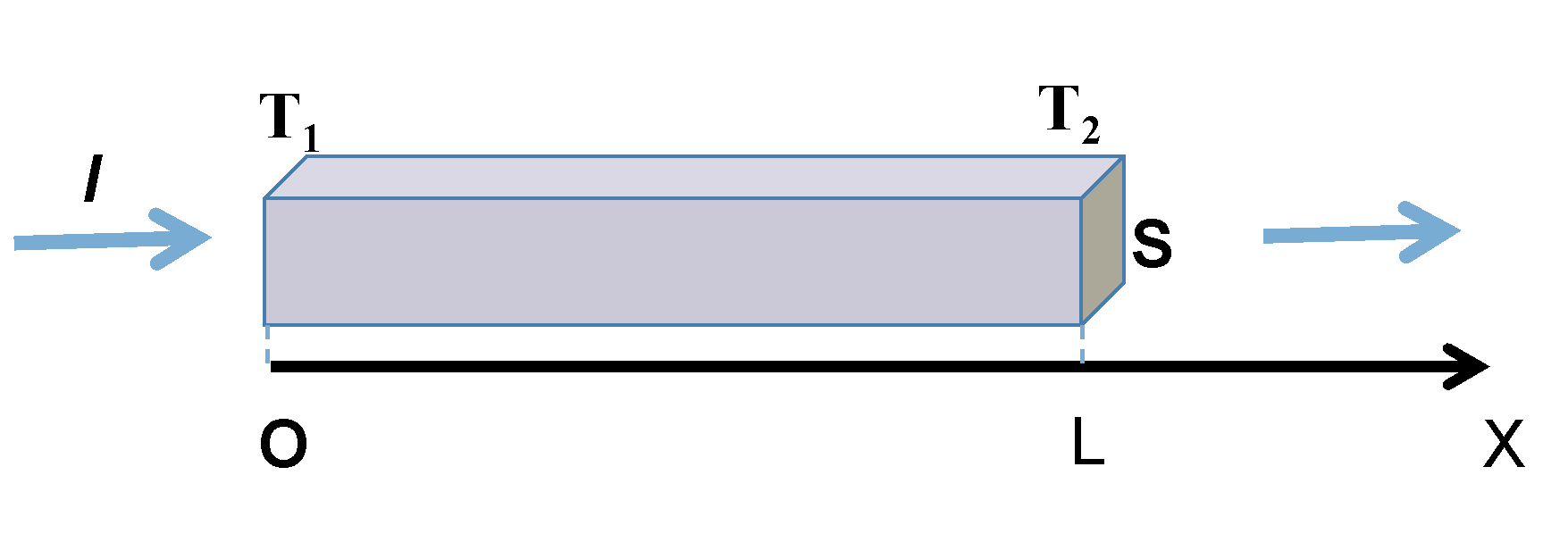
Тепловой поток $q(x)$, т.е. количество теплоты, проходящее по нормали к площадке $S$ в единицу времени, описывается законом Фурье (одномерный случай):

$$q(x)=-kS\frac{dT(x)}{dx}$$

где $k$ — коэффициент теплопроводности, а $S$ — площадь поперечного сечения.

A1  ^0.75 Найдите распределение температуры $T(x)$ вдоль стержня. Считайте, что распределение стационарно, а также что нет потерь тепла в окружающую среду.

Примечание. Уравнение вида $\cfrac{d^2T(x)}{dx^2}=a$ имеет решение вида

$T(x)=\cfrac{1}{2}\ ax^2+C_1x+C_2$, где $C_1$ и $C_2$ — постоянные, определяемые из граничных условий.

A2  ^1.00 Найдите тепловой поток $q(x)$ в произвольной точке $x$, а также рассчитайте его на концах: $q(0)$ и $q(L)$.

Связь коэффициентов Зеебека и Пельтье

Рассмотрим термопару (рис. 1b), у которой коэффициент Зеебека равен $\alpha$. Ее коэффициенты Пельтье равны $\pi_1$ и $\pi_2$ на горячем ($T_1$) и холодном ($T_2$) спаях термопары соответственно. Выделением джоулева тепла можно пренебречь. Считайте, что электронный газ в проводниках термопары совершает идеальный цикл.

B1  ^0.25 Какую тепловую мощность $q_1$ получает газ от нагревателя температурой $T_1$?

B2  ^0.25 Какую тепловую мощность $q_2$ газ отдает холодильнику температурой $T_2$?

B3  ^0.50 Какая полная электрическая полезная мощность $P$ производится электронным газом, если коэффициент Зеебека равен $\alpha$?

B4  ^0.50 Выразите коэффициент Пельтье $\pi$ на спае термопары через коэффициент Зеебека $\alpha$ и температуру спая $T$.

Термоэлектрический генератор

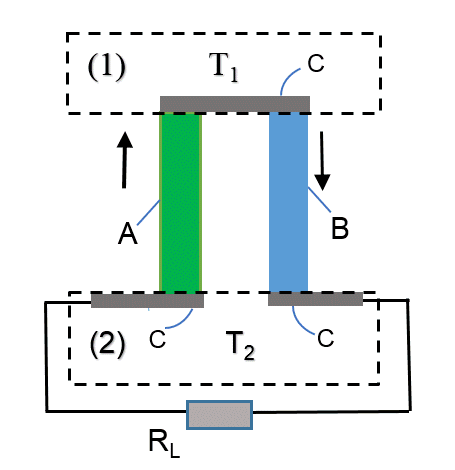
Внимание! Здесь и далее коэффициент Пельтье $\pi$ примите равным $\alpha T$. Также везде нужно будет учитывать выделяющееся джоулево тепло.

Термопара состоит из двух проводников $A$ и $B$ одинаковой длины $L$ (рис. 4). Параметры проводников, соответственно, равны: площади поперечного сечения $S_A$ и $S_B$, удельные сопротивления $\rho_A$ и $\rho_B$, коэффициенты теплопроводности $k_A$ и $k_B$. Нижние концы стержней подключены к нагрузке $R_L$. Параметры термопары таковы: $\alpha$ — коэффициент Зеебека, $R=\cfrac{\rho_AL}{S_A}+\cfrac{\rho_BL}{S_B}$ — ее внутренее сопротивление, $K=\cfrac{k_AS_A}{L}+\cfrac{k_BS_B}{L}$ — ее коэффициент теплопроводности. Верхний спай термопары поддерживается при температуре $T_1$, нижний — при $T_2$, причем $T_1>T_2$. Обозначим $q_1$ полную тепловую мощность, забираемую у нагревателя ($T_1$), а $q_2$ — полную тепловую мощность, получаемую холодильником ($T_2$).

C1  ^0.50 Выразите $q_1$ и $q_2$ через параметры термопары $\alpha, K, R$, температуры $T_1, T_2$ и силу тока $I$.

КПД термоэлектрического генератора определяется как $\eta={P_L}/{q_1}$, где $P_L$ — мощность, выделяющаяся на нагрузке. Отношение сопротивлений нагрузки и термопары обозначается $m={R_L}/{R}$.

C2  ^0.75 Выразите КПД $\eta$ генератора через параметры термопары $\alpha, K, R$, температуры $T_1, T_2$ и отношение сопротивлений $m$.

При производстве термоэлектрических генераторов необходимо удовлетворить следующим условиям: а) минимизировать сопротивление, чтобы уменьшить выделение джоулева тепла; б) обеспечить низкую теплопроводность, чтобы уменьшить теплопередачу между спаями, и в) сохранять большую разность температур. Совместно это характеризуется показателем качества термопары $Z={\alpha^2}/{KR}$.

C3  ^0.25 Выразите КПД $\eta$ генератора через $Z$, КПД идеального цикла Карно $\eta_c=\frac{T_1-T_2}{T_1}$, температуру $T_1$ и $m$.

Максимальный КПД генератора

D1  ^0.25 Обозначим $\eta_P$ КПД генератора, когда на нагрузке выделяется максимальная мощность $P_L=P_{\mathrm{max}}$. Выразите $\eta_P$ через $Z, T_1, T_2$.

D2  ^0.75 КПД генератора достигает максимума $\eta=\eta_{\mathrm{max}}$ при некотором значении отношения сопротивлений $m=M$. Выразите это $M$ через $Z, T_1, T_2$.

D3  ^0.25 Выразите максимальный КПД $\eta_{\mathrm{max}}$ через $Z, M, T_1, T_2$.

Максимальный показатель качества термопары

Увеличение показателя качества термопары приводит к увеличению КПД генератора. При производстве термопар площади поперечного сечения $S_A$ и $S_B$ проводников подбираются так, что показатель качества получается максимальным $Z=Z_m$.

E1  ^0.50 Найдите отношение площадей поперечного сечения $S_A/S_B$ проводников, когда показатель качества термопары максимален. Ответ выразите через $\rho_A, \rho_B, k_A, k_B$.

E2  ^0.25 Выразите максимальный показатель качества термопары $Z_m$ через $\alpha, \rho_A, \rho_B, k_A, k_B$.

Оптимальный КПД генератора

Если показатель качества термопары и электрическая мощность, выделяющаяся на нагрузке, максимальны одновременно, то такой режим работы генератора называется оптимальным. Обозначим $\eta_{opt}$ КПД такого генератора.

Пусть нагреватель имеет температуру $T_1=423$ К, а холодильник — $T_2=303$ К.

F1  ^0.50 Вычислите значение $\eta_{opt}$ термоэлектрического генератора, который изготовлен из материалов, характеристики которых приведены в Таблице 1.

Сравните вычисленное значение с КПД идеальной тепловой машины $\eta_c$.

F2  ^0.25 Вычислите значение максимального КПД $\eta_{\mathrm{max}}$ термоэлектрического генератора, изготовленного из указанных материалов.

Часть II. Термоэлектрический холодильник (2.5 балла)

Термопара с параметрами $\alpha, K, R$, определенными в пункте «Термоэлектрический генератор», используется как холодильник (рис. 5).

Верхний спай термопары соприкасается с теплым резервуаром начальной температуры $T_1$. Резервуар теплоизолирован от окружающей среды, и его хотят охлаждать. Нижние концы проводников всегда поддерживаются при температуре $T_2$ и подключены к источнику тока. Направление тока, текущего через спай термопары, такое, что у верхнего, теплого, резервуара теплота поглощается, а выделяется внизу.

G1  ^0.25 $q_C$ — это полная тепловая мощность, которая отбирается от теплого резервуара. Выразите $q_C$ через параметры термопары $\alpha, K, R$ и $T_1, T_2, I$.

G2  ^0.50 Найдите максимальную разность температур $\Delta T_{\max}=T_2-T_{1\min}$, которой можно достичь, используя термоэлектрический холодильник. Ответ выразите через показатель качества термопары $Z$ и наинизшую температуру $T_{1\min}$ верхнего резервуара, до которой его можно охладить.

Термопара изготовлена из материалов $A$ и $B$ с наилучшим показателем качества $Z_m$ (найденным в части А). Эта термопара используется в качестве холодильника.

H1  ^0.25 Найдите и рассчитайте численное значение минимальной температуры $T_{1\min}$ верхнего резервуара, если нижние концы поддерживаются при температуре $T_2=300$ К.

H2  ^0.50 Найдите и рассчитайте численное значение рабочей силы тока $I_w$ холодильника, когда верхний резервуар можно охладить до минимальной температуры $T_{1\min}$. Нижние концы поддерживаются при температуре $T_2=300$ К. Считайте, что площади поперечного сечения равны $S_A=S_B=10^{-4}$ м$^2$.

Холодильный коэффициент

Когда разность температур меньше своего возможного максимального значения $\Delta{T_{\max}}$, вводится холодильный коэффициент. Он определяется как $\beta={q_C}/{P}$, где $P$ — подводимая электрическая мощность.

I1  ^0.50 Выразите холодильный коэффициент $\beta$ через параметры термопары $\alpha, K, R$ и $T_1, T_2, I$.

I2  ^0.25 Когда холодильный коэффициент достигает максимального значения $\beta_{\mathrm{max}}$, сила тока, текущего через термопару, равна $I_{\beta}$. Выразите $I_{\beta}$ через параметры термопары $\alpha, k, R$ и $T_1, T_2$.

I3  ^0.25 Найдите максимальное значение холодильного коэффициента $\beta_{\mathrm{max}}$.