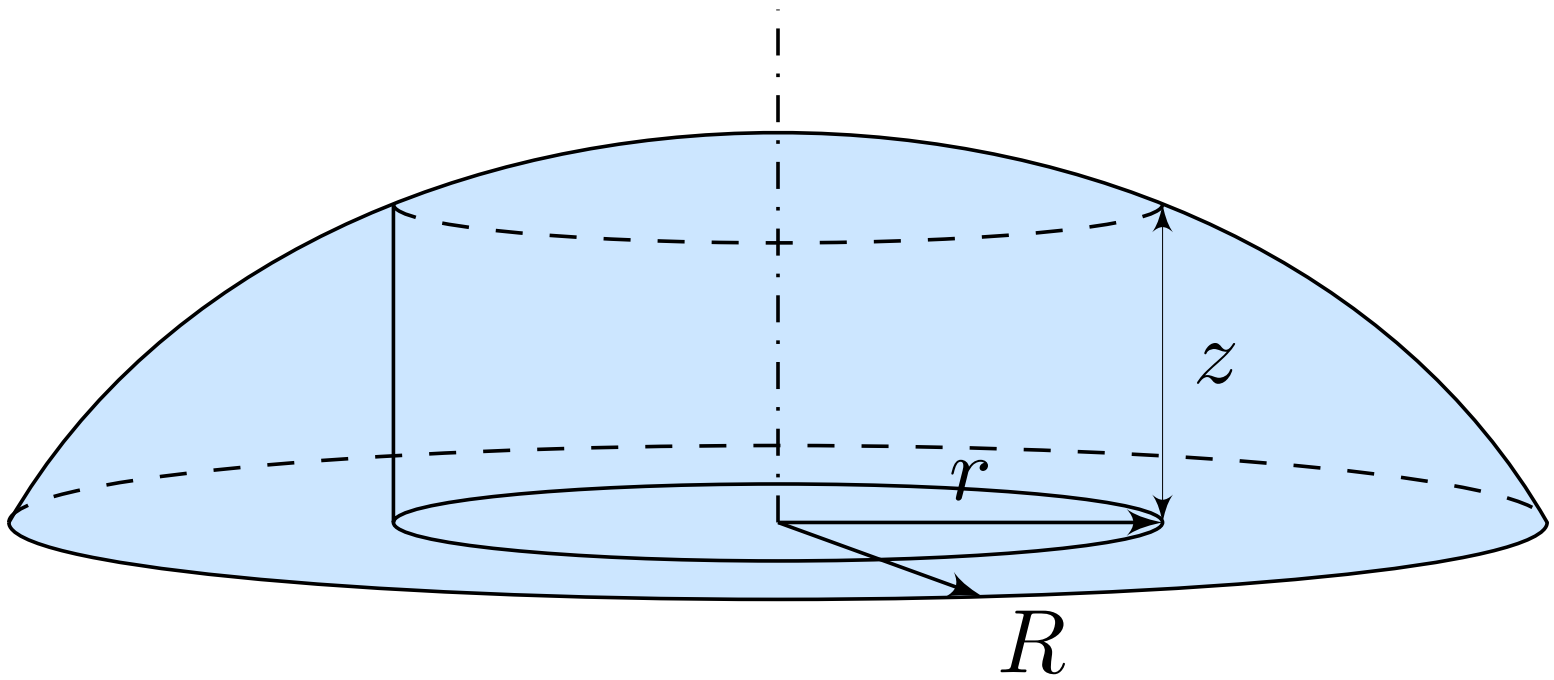
Широко известен общий физический принцип — всякая система стремится к уменьшению своей потенциальной энергии, а устойчивому положению равновесия соответствует состояние с минимальным ее значением.
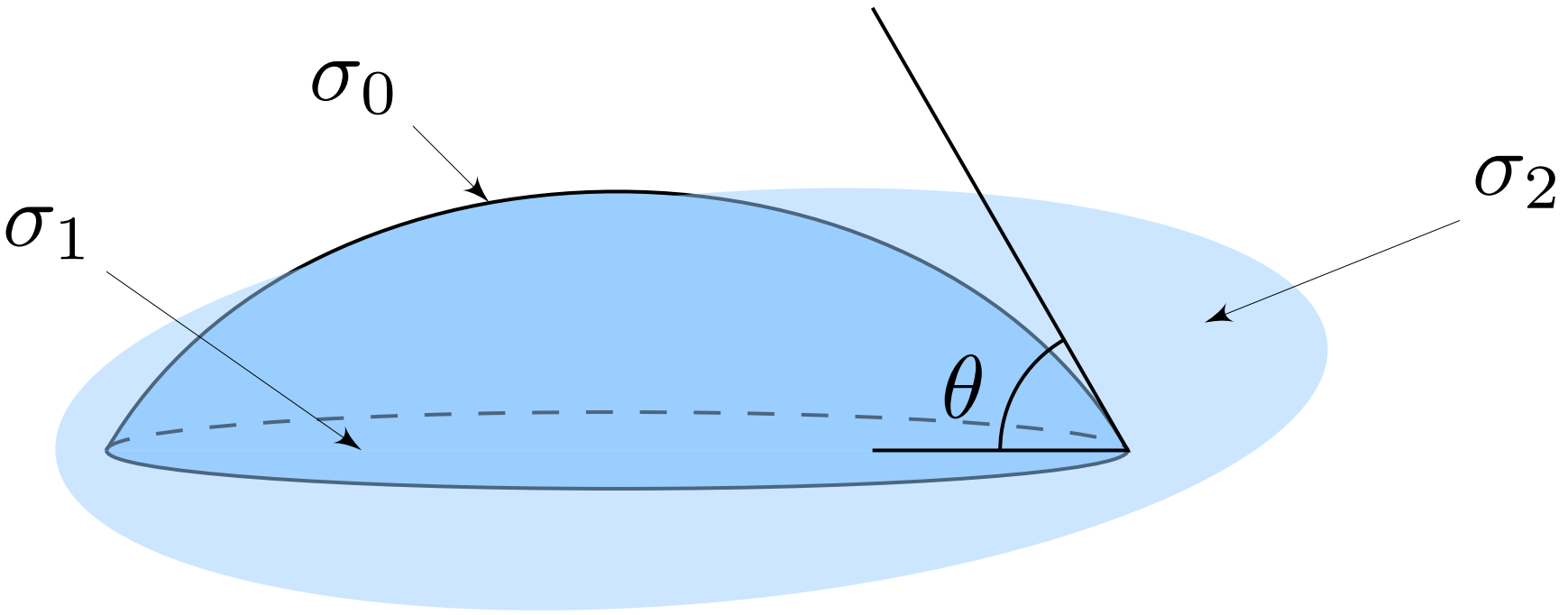
$$\Delta U_S=-\sigma_0\cos\theta\Delta S, \tag{1}$$
где $\Delta S$ — изменение площади соприкосновения жидкости с твердым телом.
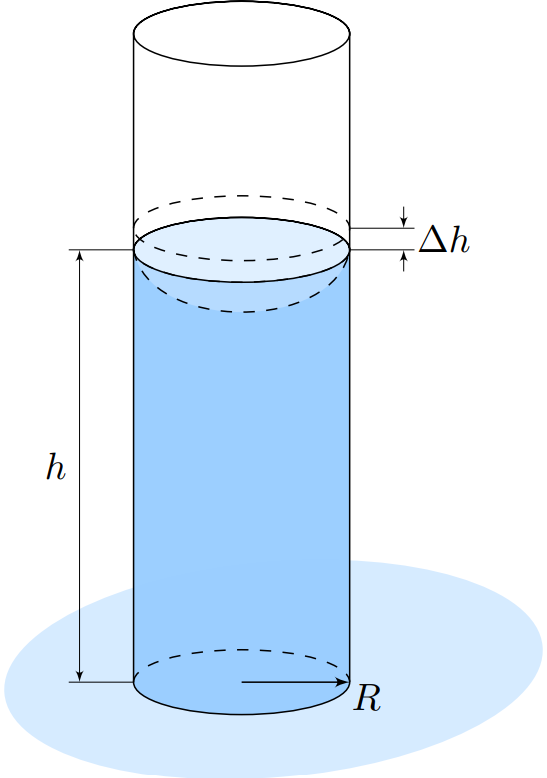
поднятии воды в трубке на малую высоту $\Delta h$.
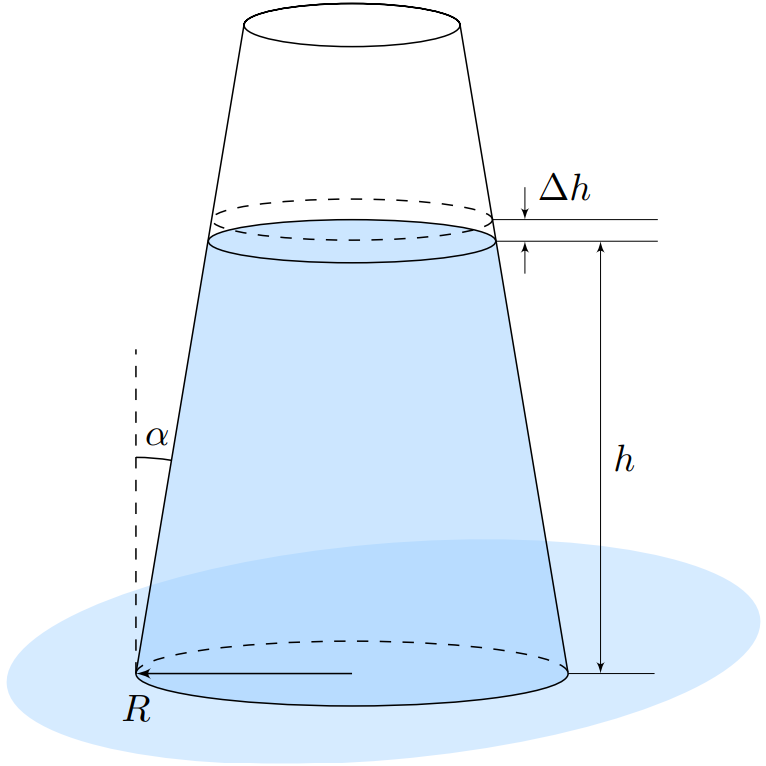
Внимание: В дальнейшем изменение поверхностной энергии на границе жидкости и воздуха не учитывайте.
Пусть уровень воды в трубке находится на некоторой высоте $h$, не обязательно соответствующей положению равновесия.
Бутылка заполнена водой и перевернута вертикально пробкой вниз. В пробке проделаны два одинаковых круглых отверстия, радиусы которых равны $R$.