
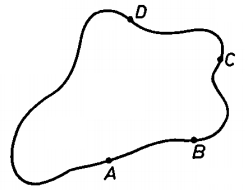
Теоретически можно показать, что удельное сопротивление материала рассчитывается по следующей формуле
$$
\rho=\cfrac{{\pi}d}{\ln2} ({R_{\text{AB,CD}}}+{R_{\text{BC,DA}}}) \cfrac{f\left(\frac{R_{\text{AB,CD}}}{R_{\text{BC,DA}}}\right)}{2},
$$
где $f$~— некая функция, которая не выражается аналитически. В этой задаче вам предстоит численно найти значения этой функции в нескольких точках, а затем вычислить удельное сопротивление пластины.
Обозначим $y=\cfrac{R_{\text{AB,CD}}}{R_{\text{BC,DA}}}$, тогда выражение для удельного сопротивления принимает вид
$$
\rho=\cfrac{{\pi}d}{\ln2} {R_{\text{BC,DA}}} (y+1) \frac{f(y)}{2}
$$
Из теоретических выкладок можно получить, что функция $f(y)$ удовлетворяет соотношению
$$
\cfrac{y-1}{y+1}=\cfrac{f(y)}{\ln2}~\text{arch} \left(\cfrac{1}{2}\exp\left(\cfrac{\ln2}{f(y)}\right)\right)
$$
Для удобства обозначив $x=\cfrac{\ln2}{f(y)}$, можно получить равносильную систему уравнений для нахождения удельного сопротивления, которой и нужно пользоваться при дальнейшем решении задачи
$$
\rho={{\pi}d} {R_{\text{BC,DA}}} (y+1) \frac{1}{2x},
$$
$$
\cfrac{y-1}{y+1}=\cfrac{1}{x} \text{arch}\left(\cfrac{\text{e}^x}{2}\right).
$$
Примечание. Гиперболические и обратные гиперболические функции задаются следующими формулами: $$\text{sh}~x=\cfrac{\text{e}^x-\text{e}^{-x}}{2},\quad\text{ch}~x=\cfrac{\text{e}^x+\text{e}^{-x}}{2},$$ $$\text{arsh}~x=\ln(x+\sqrt{x^2+1}),\quad\text{arch}~x=\ln(x+\sqrt{x^2-1}).$$
Найдите $\alpha$ и $\beta$. Ответ выразите через $y$.
Полупроводники бывают двух типов~— собственные и примесные. Критерий их разделения следующий: если в собственных полупроводниках проводимость осуществляется в первую очередь за счет движения собственных электронов, то в примесном полупроводнике на проводимость влияют атомы примеси.
В этой части задачи рассматривается полупроводник $n$-типа, в котором на проводимость влияют доноры. В зависимости от температуры полупроводника, доноры могут являться как основным, так и слабым источником проводимости.
При повышении температуры в полупроводнике протекают процессы ионизации доноров и перехода собственных электронов из валентной зоны в зону проводимости. При низких температурах $kT\ll{E_d}$, ($E_d$~— энергия ионизации донора), и переходом электронов в зону проводимости можно пренебречь. Поэтому основным источником проводимости являются ионизированные доноры. Зависимость концентрации ионизированных доноров в таком режиме следующая
$$
n={C_1}T^{3/4}\exp\left(-\frac{{E_d}}{2kT}\right)
$$
Процесс перехода от низких температур к высоким сопровождается областью истощения, когда практически все атомы примеси ионизируются, а концентрация свободных носителей заряда остается постоянной в широком диапазоне температур. Температура перехода в область истощения называется $T_i$.
В области высоких температур собственные электроны приобретают достаточную энергию для перехода в зону проводимости, и концентрация свободных электронов начинает резко возрастать. В этой области температур, называемой областью собственной проводимости, основной вклад в проводимость вносят собственные электроны. Температура перехода в область собственной проводимости обозначается $T_s$. Концентрация свободных электронов в области собственной проводимости зависит от температуры по следующему закону
$$
n={C_2}T^{3/2}\exp\left(-\frac{\Delta{E_g}}{2kT}\right),
$$
где $\Delta{E_g}$~— ширина запрещенной зоны.