1  ^?? Определите сопротивление $R$ выданного Вам резистора.

Внимание! Приведённые ниже значения получены на авторской установке и могут отличаться от значений, полученных жюри!

Переключим один из приборов в режим вольтметра (режим ''200m''), другой — в режим омметра (режим «2000k») и соединим их друг с другом. В этом случае вольтметр покажет напряжение $U_V=129{,}8\ мВ$, а омметр измерит сопротивление вольтметра $R_V=996\ кОм$.

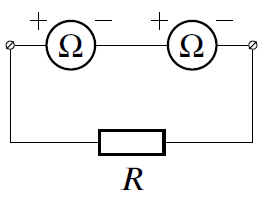
Сумма показаний омметров, $R_{\Omega1}$ и $R_{\Omega2}$, равна искомому сопротивлению резистора
$$R=R_{\Omega1}+R_{\Omega2}=1507\ кОм+1510\ кОм=3017\ кОм\approx 3020\ кОм.$$
Погрешность определения суммы можно оценить как $6\ кОм$, то есть $0{,}2\%$. Если же показания приборов «скачут» в процессе измерения, то к полученной оценке необходимо добавить сумму амплитуд этих колебаний на обоих приборах. Так, например, при колебаниях показаний каждого прибора в пределах $\pm 5\ кОм$, итоговая погрешность данного метода будет равна $16\ кОм$ или $0{,}53\%$.

Способ 2. Соединим резистор $R$ и вольтметр параллельно и подключим к ним омметр. Он покажет $R'=749\ кОм$. Отсюда найдём $R$:
$$\frac{1}{R}+\frac{1}{R_V}=\frac{1}{R'} \quad\Rightarrow\quad R=\frac{R_VR'}{R_V-R'}=\frac{996\cdot 749}{247}\ кОм=3020\ кОм.$$
Относительная погрешность такого способа:
$$\varepsilon_{R}=\varepsilon_{R'}+\varepsilon_{R_V}+\frac{\Delta R_V+\Delta R'}{R_V-R'}=\frac{3}{749}+\frac{3}{996}+\frac{6}{247}\approx 3{,}1\%.$$

2  ^?? Определите значения напряжения $U_0$ и сопротивления $r$ на принципиальной схеме для выданного Вам мультиметра в режиме омметра (диапазон «2000k»).

Рассмотрим последовательное соединение омметра, вольтметра и резистора $R$. Омметр находится в режиме «2000k», вольтметр — в режиме «200m». Омметр при этом будет зашкаливать, но вольтметр покажет значение напряжения (по модулю) $U_V'=51{,}6\ мВ$ (знак минус может возникнуть из-за полярности подключения).

Используя принципиальную схему омметра, получим, что собранная цепь представляет собой последовательное соединение источника и трёх резисторов: $r$, $R$ и $R_v$. Напряжение на $R_V$ будет равно
$$U'_V=\frac{U_0R_V}{r+R+R_V}.$$
Аналогично, если омметр и вольтметр подключены напрямую (без резистора $R$) напряжение на вольтметре составит
$$U_V=\frac{U_0R_V}{r+R_V}.$$
Отсюда найдём, что
$$\frac{1}{U'_V}-\frac{1}{U_V}=\frac{R}{U_0R_V} \quad\Rightarrow\quad U_0=\frac{U_VR/R_V}{U_V/U'_V-1}=\frac{393{,}2\ мВ}{129{,}8/51{,}6-1}\approx 259\ мВ.$$

Сопротивление $r$, соответственно, равно
$$r=\frac{U_0R_V}{U_V}-R_V=\frac{R}{U_V/U'_V-1}-R_V=\frac{3017\ кОм}{129{,}8/51{,}6-1}-996\ кОм\approx 995\ кОм.$$

3  ^?? Оцените погрешность полученных значений $R$, $U_0$ и $r$.

Погрешность значения сопротивления $R$ определена выше, в пункте 1.

Для оценки погрешностей $U_0$ и $r$ найдём относительную погрешность значения выражения $k=U_V/U'_V-1$:
$$\varepsilon_k=\frac{\Delta (U_V/U'_V)}{k}=\frac{U_V/U'_V\cdot(\varepsilon_{U_V}+\varepsilon_{U'_V})}{k}=\frac{2{,}516\cdot (0{,}3/129{,}8+0{,}3/51{,}6)}{1{,}516}\approx 1{,}3\%. $$
Соответственно,
$$\varepsilon_{U_0}=\varepsilon_{U_V}+\varepsilon_{R}+\varepsilon_{R_V}+\varepsilon_{k}=
0{,}3/129{,}8+0{,}53\%+3/996+1{,}3\%=2{,}4\% \quad\Rightarrow\quad \Delta U_0\approx 6\ мВ.$$
$$\Delta r=\frac{R}{U_V/U'_V-1}\cdot(\varepsilon_{R}+\varepsilon_{k})+\Delta R_V=
57\ кОм.$$

Примечание: В данных расчётах используется значение $\varepsilon_R=0{,}53\%$, приведённое в пункте 1 (способ 1). В зависимости от метода определения $R$, используемого оборудования и метода оценки погрешностей значения могут отличаться от авторских.