

$x,{~}часть трубки$ $m^{Арх}_{закр}, ~г / V_{откр},{~}{см}^3$ $m^{Арх}_{откр}, ~г / V_{откр},{~}{см}^3$ $\frac{1}{32}$ 10 18 $\frac{2}{32}$ 19 33 $\frac{3}{32}$ 28 49 $\frac{4}{32}$ 38 66 $\frac{5}{32}$ 47 82 $\frac{6}{32}$ 56 98 $\frac{7}{32}$ 66 115 $\frac{8}{32}$ 75 131
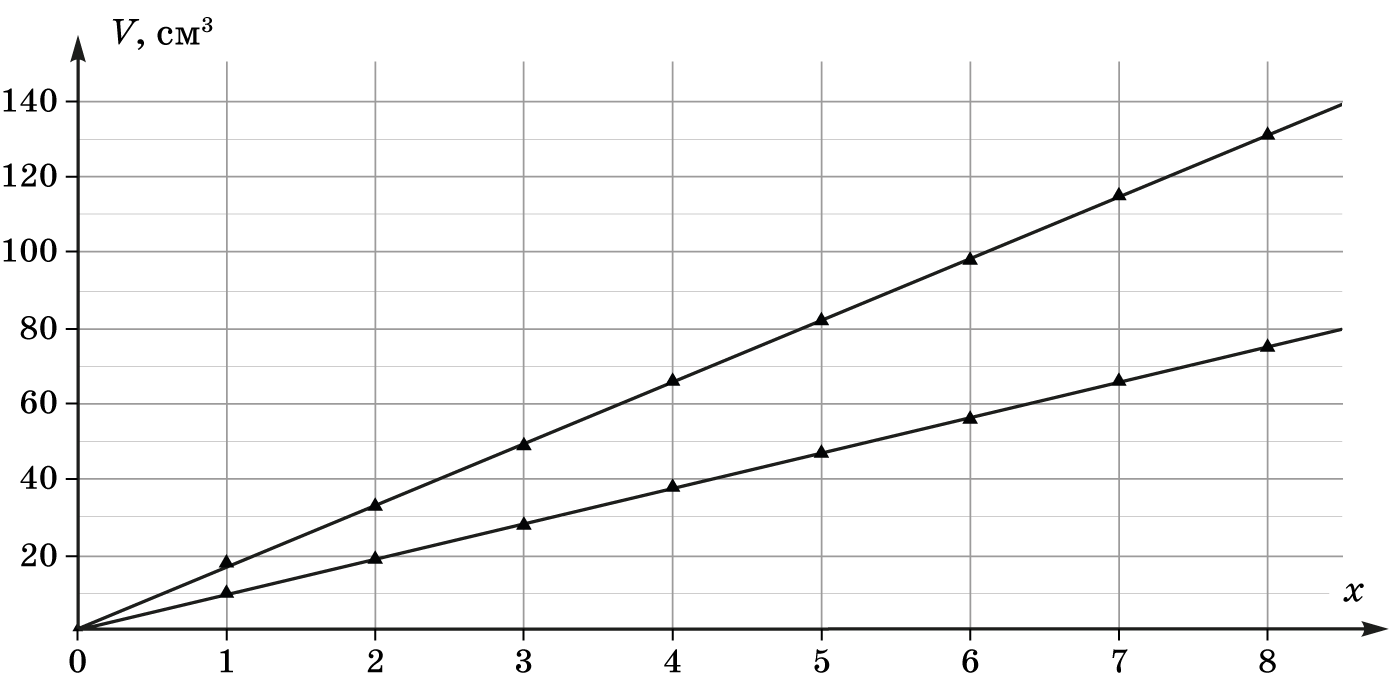
В авторской установке трубка была разделена на $32$ части. Для открытой трубки объем погруженной части $V_{откр} (x)=\frac{1}{32}Vx$, где $x$ - количество делений, погруженных в жидкость. . Угловой коэффициент $k_{откр}=\frac{1}{32} V=\frac{66}{7}{~}{см}^3$, откуда $V\approx 302{~}{см}^3$.
Аналогично проведем эксперимент для закрытой трубки.
В зависимости от количества делений, погруженных в жидкость, $l$
$$V_{откр}(x)=\left(\frac{\pi D^2}{4}-\frac{\pi d^2}{4}\right)\cdot \frac{x}{32} L;\\V_{закр}(x)=\frac{\pi D^2}{4}\cdot \frac{x}{32} L.$$
Тогда отношение угловых коэффициентов
$$\frac{k_{закр}}{k_{откр}}=\frac{D^2}{D^2-d^2}=\frac{\left(\frac{D}{d}\right)^2}{\left(\frac{D}{d}\right)^2-1}=\frac{115}{66}.$$
Окончательно получаем$\frac{D}{d}\approx1,5.$
Собираем экспериментальную установку, предложенную в условии.
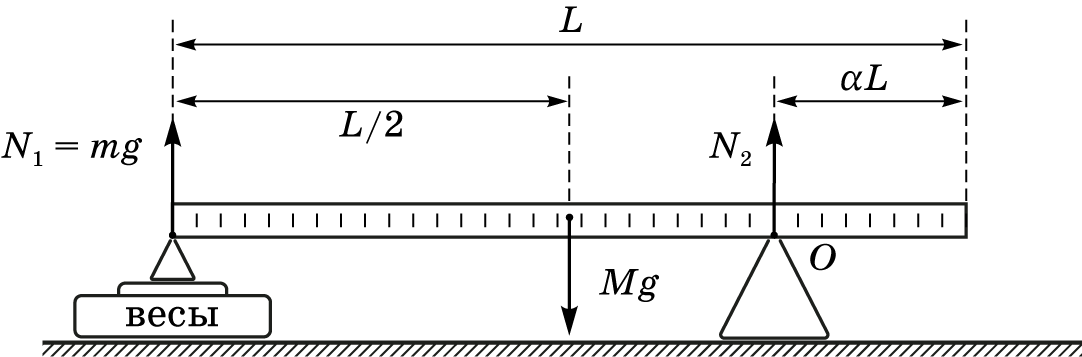
Правило моментов относительно т.$O$: $$Mg\left(\frac{L}{2}-\alpha L\right)=mg\left(L-\alpha L\right).$$
Откуда $m\left(\frac{1-2\alpha}{2(1-\alpha)}\right)=M\cdot \left(\frac{1-2\alpha}{2(1-\alpha)}\right)$ – линейная зависимость с угловым коэффициентом, равным массе трубки $M$.
$m,{~}г$ $\alpha$ $\frac{1-2\alpha}{2(1-\alpha)}$ 29 $\frac{14}{32}$ 0,11 42 $\frac{13}{32}$ 0,16 54 $\frac{12}{32}$ 0,20 64 $\frac{11}{32}$ 0,24 74 $\frac{10}{32}$ 0,27 82 $\frac{9}{32}$ 0,30 90 $\frac{8}{32}$ 0,33 98 $\frac{7}{32}$ 0,36 105 $\frac{6}{32}$ 0,39 111 $\frac{5}{32}$ 0,41 117 $\frac{4}{32}$ 0,43 122 $\frac{3}{32}$ 0,44
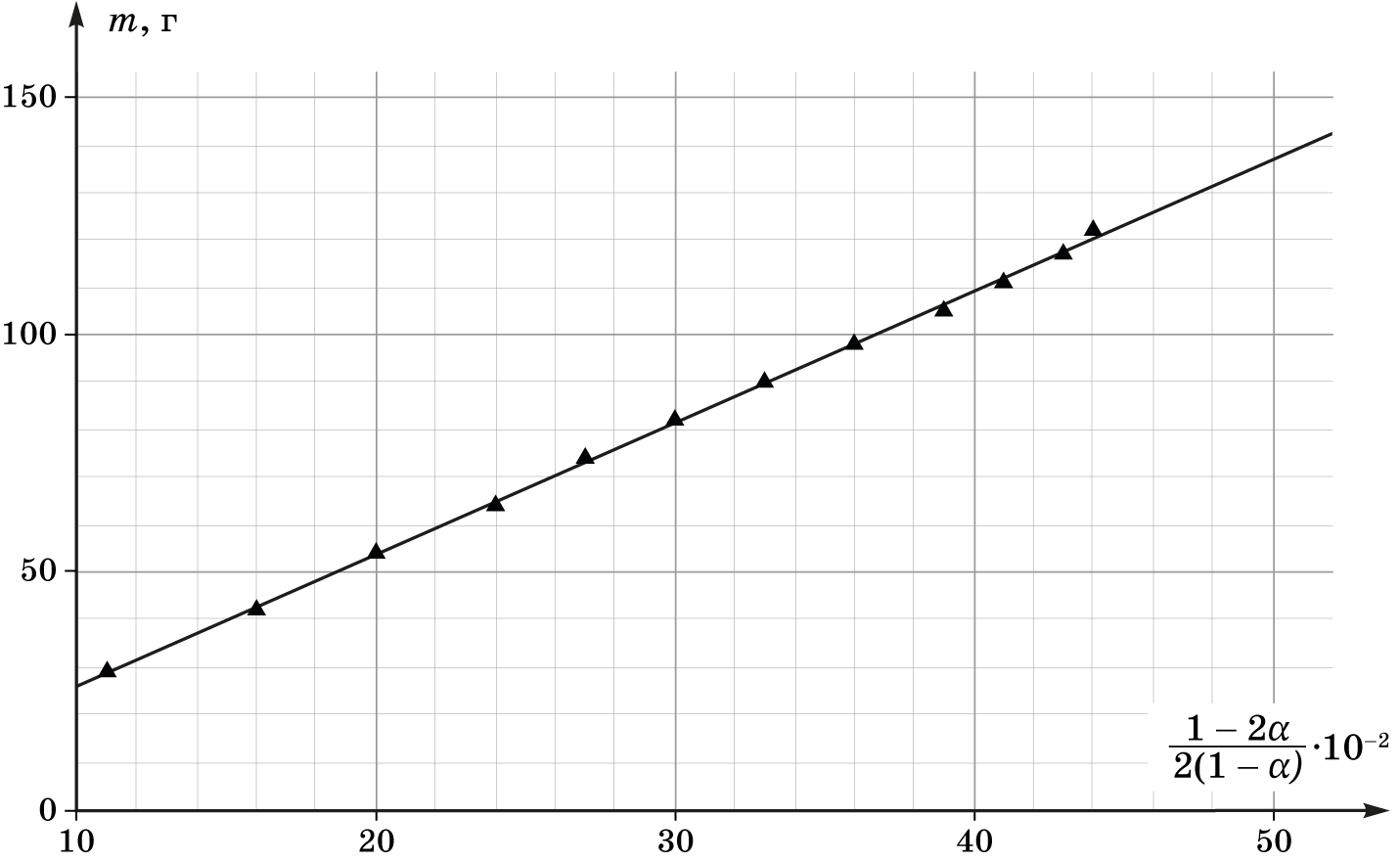
Из углового коэффициента наклона определяем массу трубку $M=274{~}г$.
Определяем плотность $\rho=\frac{M}{V}=0,91{~}\frac{г}{см^3}.$